Задачи для самостоятельного решения.

1. Рассчитать рН буферного раствора, приготовленного смешиванием 20 мл 0,2 М раствора Na₂HPO₄ и 50 мл 0,5 М раствора NaH₂PO₄. р K_a () = 6,8.

(Ответ: 6,00).

2. Рассчитать рН раствора, полученного при смешивании 1,2 л 1,2 М раствора NH₄OH и 0,6 л 0,6 М раствора NH₄Cl. K_b (NH₄OH) = 1,8·10^–5.

(Ответ: 9,67).

3. Как изменится рН ацетатного буферного раствора (объем равен 1 л), содержащего 0,1 моль CH₃COOH и 0,02 моль CH₃COONa, при добавлении 0,01 моль HCl? K_а (CН₃СООН) =1,75·10^–5.

(Ответ: уменьшится на 0,342).

4. Рассчитать буферную емкость раствора по HCl, если при добавлении к 50 мл этого раствора 2 мл соляной кислоты с концентрацией 0,8 моль/л значение рН раствора изменяется от 7,36 до 7,00.

(Ответ: 0,085 моль/(л×ед. рН))

 

ЭЛЕКТРОХИМИЯ

 

Методы измерения электрической проводимости (прямая кондуктометрия и кондуктометрическое титрование) применяют для исследования свойств лекарственных препаратов и в контроле производства различных фармацевтических продуктов.

Кондуктометрию применяют для определения общего содержания электролитов в лечебных минеральных водах, продуктах детского, диетического и парентерального питания, растворах для внутривенного вливания.

Потенциометрия – один из наиболее широко применяемых в фармации методов. Он отличается высокой точностью, воспроизводимостью, быстротой определения, не требует дорогостоящего оборудования и реактивов.

В фармацевтическом анализе его используют при определении содержания цинка в лекарственных препаратах, железа в таблетированных формах и драже. Особенно часто применяют прямую потенциометрию (рН-метрию) для определения кислотности среды. Для определения ионов щелочных металлов и аммония используют электроды с поливинилхлоридными пластифицированными мембранами на основе антибиотиков (валиномицина, лазалоцида, нонактина).

 

Электропроводность растворов электролитов

Основные уравнения

v Электрохимия – раздел физической химии, в котором изучаются физико-химические свойства ионных систем (растворов, расплавов или твердых электролитов), а также явления, возникающие на границе двух фаз с участием заряженных частиц (ионов и электронов).

 

В гальваническом элементе одна из фаз – чаще всего металл или полупроводник, другая – раствор или расплав электролита.

Различают две основные группы проводников электрического тока: проводники первого рода – металлы, электрическая проводимость которых обусловлена электронами, и проводники второго рода, обладающие ионной проводимостью – растворы и расплавы электролитов.

Количественной характеристикой способности растворов проводить ток служит электрическая проводимость. Электрическая проводимость G представляет собой величину, обратную электрическому сопротивлению:

.

(200)

Размерностью электропроводности в системе СИ является См/м или Ом^–1×м^–1. Сопротивление проводника, имеющего простую форму (например, цилиндра или прямоугольной призмы), связано с его длиной и сечением уравнением:

,

(201)

где ρ – удельное электрическое сопротивление, Ом·м; l – длина, м; S – площадь поперечного сечения, м².

 

v Удельное электрическое сопротивление это сопротивление объема раствора, находящегося между двумя параллельными электродами, имеющими площадь по 1 м² и расположенными на расстоянии 1 м друг от друга.

 

Отношение l / S называют константой кондуктометрической ячейки K _яч:

.

(202)

Вводя в уравнение (201) константу ячейки, получим:

,

(203)

или

,

(204)

где k – удельная электрическая проводимость, См/м

k = 1/ r.

(205)

Переходя от сопротивления в уравнении (204) к электропроводности (200), получим:

.

(206)

Константу ячейки определяют, используя стандартный раствор (обычно KCl), удельная электропроводность которого известна (Приложение 12).

Для этого измеряют сопротивление или электропроводность такого стандартного раствора, а затем рассчитывают константу ячейки по формуле:

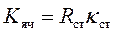
(207)

или

.

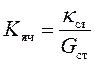(208)

Удельная электрическая проводимость k является характеристикой проводящей среды – раствора электролита.

 

v Удельная электрическая проводимость это электропроводность объема раствора, находящегося между двумя параллельными электродами, имеющими площадь по 1 м² и расположенными на расстоянии 1 м друг от друга.

 

Удельная электрическая проводимость зависит от многих факторов, и, прежде всего, от природы электролита, его концентрации, температуры и природы растворителя (рис. 49).

Рис. 49. Зависимость удельной электропроводности от концентрации электролитов

 

При равных концентрациях и прочих равных условиях наибольшей является удельная электрическая проводимость растворов сильных кислот, меньше – растворов сильных оснований, еще меньше – других электролитов, особенно низкие значения удельной электропроводности имеют растворы слабых электролитов. Высокие значения электропроводности сильных кислот и щелочей объясняются особым механизмом переноса ионов водорода Н⁺ и гидроксила ОН^– и, как следствие, более высокими подвижностями по сравнению с другими ионами (Приложение 13). В отличие от других ионов, движение ионов Н₃О⁺ и ОН^– в воде под влиянием электрического поля происходит не только за счет миграции (то есть движения в направлении поля вместе со своей гидратной оболочкой), но и эстафетным механизмом за счет перескока протонов от одной молекулы воды к другой в том же направлении. В разбавленных растворах электролитов эстафетный механизм переноса является преобладающим.

Схематически эстафетный перенос протонов по цепочке водородных связей между молекулами воды под действием электрического поля можно представить следующим образом:

 

	расстояние, на которое сместился протон
	расстояние, на которое сместился электрический заряд
до перескока H+	после перескока H+

 

После перескока протона требуется некоторое время для того, чтобы молекулы воды развернулись на 180° в исходное положение. В этом случае вновь образуется цепочка молекул воды, по которой возможен перескок следующего протона. Скорость перемещения заряда за счет эстафетного механизма больше, чем скорость движения иона гидроксония с его гидратной оболочкой под действием электрического поля.

Перенос ионов гидроксила по цепочке водородных связей между молекулами воды под действием электрического поля также происходит по эстафетному механизму:

 

	расстояние, на которое сместился протон
	расстояние, на которое сместился электрический заряд
до перескока H+	после перескока H+

 

Удельная электрическая проводимость растворов электролитов растет с концентрацией (рис. 49) до некоторых максимальных значений, что отвечает увеличению числа ионов в единице объема раствора. Достигнув максимума, удельная электрическая проводимость снижается, несмотря на дальнейший рост концентрации электролита. Подобный характер зависимости связан у сильных электролитов с уменьшением подвижности ионов из-за возрастающего по мере увеличения концентрации раствора межионного взаимодействия, а у слабых электролитов – со снижением степени электролитической диссоциации, а значит, с уменьшением числа ионов в растворе.

С удельной электрической проводимостью электролита связана молярная электрическая проводимость λ:

,

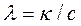(209)

где l – молярная электрическая проводимость, Ом^–1×м²×моль^–1 или См·м²/моль; k – удельная электрическая проводимость, См×м^–1; с – концентрация электролита в растворе, моль/м³.

 

v Молярная электрическая проводимость электролита (λ)равна удельной электрической проводимости его раствора с концентрацией 1 моль/м³.

 

Значение молярной электрической проводимости любого электролита при разбавлении раствора (при с → 0) увеличивается, стремясь к постоянной, характерной для каждого электролита величине, называемой предельной молярной электрической проводимостью и обозначаемой λ ⁰.

 

v Предельной молярной электрической проводимостью электролита (λ ⁰ ) называется значение его молярной электрической проводимости в бесконечно разбавленном растворе.

 

В случае сильных электролитов молярная электрическая проводимость электролита равна сумме молярных электропроводностей (или подвижностей) ионов:

(210)

или в бесконечно разбавленном растворе:

.

(211)

Для слабых электролитов это уравнение имеет другой вид:

(212)

или

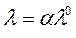
(213)

и является приближенным. Это связано с тем, что в теории Аррениуса (в которой вводится это уравнение) предполагалось, что молярные электропроводности не зависят от концентрации (то есть ), а отличие от обусловлено только неполной диссоциацией электролита.

Уравнения (210) – (212) называются уравнениями Кольрауша, в соответствии с которыми, в растворе электролита катионы и анионы переносят электрический ток независимо друг от друга.

 

v Предельная молярная электрическая проводимость l ⁰ данного электролита равна сумме предельных молярных проводимостей ионов, входящих в его состав.

 

Для разбавленных растворов сильных 1,1-валентных электролитов Кольраушем было получено эмпирическое соотношение:

(214)

хорошо согласующееся с экспериментальными данными.

Это уравнение получило обоснование в теории Дебая – Хюккеля – Онзагера, в которой снижение молярной электропроводности (подвижности) иона и электролита в целом объясняется тормозящими эффектами ионной атмосферы: электрофоретическим и релаксационным.

Электрофоретический эффект связан с тем, что ион под действием внешнего электрического поля перемещается не в неподвижной среде, а в потоке движущихся ему навстречу противоионов.

Релаксационный эффект торможения обусловлен конечным временем разрушения (релаксации) ионной атмосферы. В результате этого центр ионной атмосферы в неравновесных условиях оказывается смещенным на некоторое расстояние от положения движущегося центрального иона. Таким образом, на центральный ион действует электростатическая возвращающая сила, которая и замедляет его движение.

Уравнения теории Дебая – Хюккеля – Онзагера для молярной подвижности отдельного иона:

(215)

и электролита в целом

.

(216)

по своему виду совпадают с уравнением (214) Кольрауша для зависимости молярной электропроводности электролита от концентрации. В водных растворах при температуре 25°С уравнение Дебая – Хюккеля – Онзагера (216) принимает вид:

,

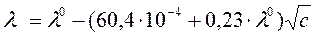(217)

где размерность l – См·м²/моль, а размерность с – моль/л. Уравнение (217) применимо в еще более разбавленных растворах (с < 0,001), чем уравнение 1-го приближения теории Дебая – Хюккеля для коэффициента активности. Для расчета мольных электропроводностей электролитов в более широком диапазоне концентраций необходимо использовать справочные данные (Приложение 14).

Используя уравнение (213) Кольрауша для слабой одноосновной кислоты

HA H⁺ + А^–

можно вывести уравнение, связывающее молярную электропроводность электролита и его концентрацию. Для этого, вводя в уравнение для константы диссоциации:

(218)

степень диссоциации, получим уравнение закона разбавления Оствальда:

.

(219)

Исключая из этого уравнения степень диссоциации, используя уравнение (213), получим:

(220)

или

(221)

Если степень диссоциации кислоты мала и 1 >> a, то уравнения (219) и (220) упрощаются:

(222)

и

.

(223)

Предельная подвижность иона является специфической величиной для данного вида ионов. Она зависит от заряда иона, радиуса сольватированного иона в растворе, а также природы растворителя, его вязкости и температуры и не зависит от природы другого иона в данном электролите:

(224)

где – предельная молярная электрическая проводимость иона; e ₀ – абсолютная величина заряда электрона; N _A – число Авогадро; h – коэффициент динамической вязкости растворителя; r_i – радиус сольватированного иона в растворе.

Электрическая проводимость многих неводных растворов значительно ниже проводимости водных растворов, что объясняется меньшей степенью диссоциации электролитов в растворителях c малой относительной диэлектрической проницаемостью e (диэлектрическая проницаемость подавляющего большинства растворителей меньше, чем воды (78,3 при 25°С).

Другим фактором, определяющим электрическую проводимость раствора, является вязкость растворителя h (уравнение (224)). Увеличение вязкости растворителя приводит к снижению скорости движения иона и его подвижности. Ионы, имеющие больший радиус в растворе, менее подвижны.

Примеры решения задач

1. Для приготовления 0,800 л раствора в воде растворили 0,759 г гидроксида калия. Сопротивление кондуктометрической ячейки с этим раствором равно 184 Ом. Расстояние между электродами в ячейке ¾ 160 см. Площадь каждого электрода ячейки составляет 0,00200 м². Рассчитать молярную электрическую проводимость раствора KОН.

 

Решение:

Рассчитаем удельную электропроводность раствора KОН по уравнению (204), подставляя в него уравнение (202) для константы кондуктометрической ячейки

Рассчитаем концентрацию KОН в растворе

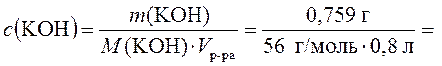
Для расчета молярной электрической проводимости используем уравнение (209)

.

 

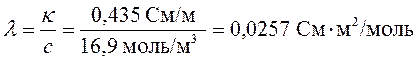2. Рассчитать значение рН желудочного сока человека, если молярная электрическая проводимость его при 37^оС равна 370 См×см²/моль, а удельное сопротивление – 0,90 Ом×м. Предположить, что в желудочном соке других электролитов, кроме HCl, нет.

 

Решение:

Рассчитаем по уравнению (205) удельную электропроводность желудочного сока

Рассчитаем концентрацию хлороводородной кислоты в желудочном соке, используя уравнение (209)

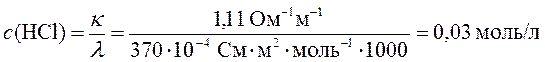
Рассчитаем рН желудочного сока, пренебрегая различием между активностью и концентрацией (полагая коэффициент активности равным 1)

рН = –lg a (H⁺)» –lg[H⁺] = –lg[HCl] = –lg0,03 = 1,52

 

3. Удельная электрическая проводимость насыщенного раствора AgBr равна 11,1×10^–6 См/м. Найти константу растворимости соли, если l ⁰(Ag⁺) = 61,9×10^–4 Cм×м²/моль; l ⁰(Br^–) = 78,4×10^–4 Cм×м²/моль; k (H₂O) = 2,0×10^–6 См/м.

 

Решение:

Определим удельную электрическую проводимость AgBr:

k (AgBr) = k _р-ра(AgBr) – k (H₂O) = (11,1 – 2,0)×10^–6 =

= 9,1×10^–6 См/м

l ⁰(AgBr) = l ⁰(Ag⁺) + l ⁰(Br^–) = (61,9 + 78,4)×10^–4 =

= 140,3×10^–4 См×м²/моль

Насыщенный раствор малорастворимой соли можно с хорошей точностью считать бесконечно разбавленным раствором, тогда:

l (AgBr) = l ⁰(AgBr),

Растворимость бромида серебра для случая, рассматриваемого в задаче, совпадает с его концентрацией, которую рассчитаем из уравнения (209)

Константа растворимости K_s (AgBr) бромида серебра, диссоциирующего по реакции

AgBr Ag⁺ + Br^–,

равна

K_s (AgBr) = [Ag⁺]×[Br^–]

Концентрация растворенного электролита при условии его полной диссоциации совпадает с концентрациями ионов серебра и брома

S (AgBr) = [Ag⁺] = [Br^–]

Тогда, подставляя значение растворимости в уравнение для константы растворимости, получим

K_s (AgBr) = S ² = (6,48×10^–7)² = 4,21×10^–13 (моль/л)²

 

4. Молярная электропроводность цианоуксусной кислоты следующим образом зависит от ее концентрации в водном растворе при 298 К:

 

с, моль/л×103		0,4660	1,856	7,335
l, Ом–1×см2/моль	386,1	347,0	282,6	193,9

 

Рассчитать среднее значение константы диссоциации K_a цианоуксусной кислоты.

Решение:

Воспользуемся уравнением (221)

Подставляя последовательно данные из условия, рассчитаем значения константы и найдем ее среднее значение

 

5. Рассчитать удельную электрическую проводимость 0,1 М раствора уксусной кислоты при 25^оС (K_a (СН₃СООН) = 1,75×10^–5 моль/л).

 

Решение:

Рассчитаем, предполагая, что степень диссоциации мала по сравнению с 1, степень диссоциации кислоты по уравнению (222)

Действительно, степень диссоциации составляет приблизительно 1% от 1, следовательно, предположение о малости a справедливо, и уравнение для расчета было выбрано правильно. Рассчитаем предельное значение молярной электропроводности кислоты, используя уравнение (211) Кольрауша

l ⁰(СН₃СООH) = l ⁰(Н⁺) + l ⁰(СН₃СОО^–) = 349,8 + 40,9 =

= 390,7×10^–4 См×м²/моль

Рассчитаем по уравнениям (213) и (209) молярную электропроводность кислоты и удельную электропроводность раствора кислоты, переводя концентрацию из моль/л в моль/м³.

l = 0,0132×390,7×10^–4 = 5,15×10^–4 См×м²/моль

k = 5,15×10^–4×0,1×1000 = 0,05 См/м

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: