 |
Выражение (2.27) можно записать в виде 1 глава
|
|
|
|
. (2.28)
Очевидно, чем больше скорость фильтрации, тем больше гидравлическое давление. То же можно сказать и про гидравлический градиент.
В практическом отношении гидравлическое давление имеет большое значение. От величины гидравлического давления зависят устойчивость откосов земляных масс, прочность грунтов, взвешивание части сооружения, расположенной ниже уровня грунтовых вод и т.д.
Если грунт находится в водонасышенном состоянии, то по закону Архимеда на него действует гидростатическое давление, равное весу вытесненной воды, т.е. грунт становится как бы легче. Удельный вес взвешенного в воде грунта определяется по формуле (см. (2.14) в п. 2.2.3):
. (2.29)
При вертикальной фильтрации вода движется снизу вверх, при этом вода будет оказывать на грунт гидродинамическое давление, равное (2.27).
На частицы грунта, т.е. на скелет, действует и сила тяжести. Если 
, то частицы грунта могут перемещаться, т.е. образуется гидродинамический выпор или фильтрационный выпор. Очевидно, что для равновесия необходимо, чтобы 
или 
, отсюда:
. (2.30)
Гидравлический градиент, при котором возможен выпор, называется критическим градиентом напора. При расчетах грунта на выпор необходимо вводить коэффициент запаса, чтобы не было выпора грунта от гидродинамического давления. Тогда формула (2.30) запишется:
, (2.31)
где k – коэффициент запаса, принимаемый больше единицы.
Движение воды может приводить к процессам,осложняющим строительство. К ним в частности относятся процессы суффозии и кольматации грунта.
Суффозия заключается в том, что движущийся поток воды в грунтах (особенно в сыпучих) может увлекать за собой мелкие частицы, которые оседают в каких-либо частях массива и кольматируют (закупоривают поры) или выносятся на поверхность. В результате суффозии может происходить увеличение пористости грунта, а, соответственно, и возрастание скорости фильтрации. Это приводит к дальнейшему развитию процесса. При этом скелет грунта может быть ослабленным, что приведет к его разрушению, образованию воронок размыва.
|
|
|
Кольматация же в связи с отложением мелких частиц вблизи открытой поверхности, вызывает уменьшение пористости и снижение водопроницаемости грунта, что отрицательно влияет на дренажные устройства, используемые для отвода воды. Это приводит их к постепенному выходу из строя.
Суффозионная устойчивость грунта зависит от его гранулометрического состава, градиента напора, скорости фильтрации, напряжений в скелете грунта и определяется опытным путем.
2.6. Особенности физических свойств мерзлых грунтов
Мерзлыми называют грунты, если они имеют нулевую или отрицательную температуру и содержат хотя бы небольшое количество льда. Как отмечалось выше, мерзлые грунты состоят из 4-х фаз [14]: твердой, жидкой, газообразной и льда.
Лед, находящийся в порах грунта, оказывает цементирующее действие на минеральный скелет (лед-цемент), связывает его и придает мерзлому грунту повышенную прочность. Кроме того, лед может присутствовать в мерзлом грунте в виде ледяных включений - линз различного размера и ориентации.
В мерзлых грунтах, наряду со льдом, всегда содержится некоторое количество незамерзшей воды. Свободная вода замерзает в диапазоне температур от 0 °C в сыпучих грунтах до -1,5 °C в глинистых (температура начала замерзания свободной воды). Прочносвязанная вода замерзает полностью при температуре –170° С (см. п. 2.1.3). Опытами установлено, что даже незначительному изменению температуры соответствует определенное изменение количества воды в жидком виде. Это так называемый принцип равновесного состояния воды и льда в мерзлых грунтах. Этот принцип имеет большое значение в физике и механике промерзающих, мерзлых и оттаивающих грунтов.
|
|
|
По степени сцементированности льдом мерзлые грунты подразделяются на твердомерзлые, пластичномерзлые и сыпучемерзлые [26]. В твердомерзлых грунтах незамерзшей воды мало, деформируемость малая, разрушение хрупкое. Пластичномерзлые грунты содержат много незамерзшей воды, поэтому обладают вязкими свойствами, под нагрузкой существенно сжимаются. К пластичномерзлым грунтам относятся такие, температура которых: для песков пылеватых выше –0,3°С; супесей выше –0,6°С; суглинков выше –1°С; глин выше -1,5°С. Если температура будет ниже этих значений, то грунты переходят в твердомерзлое состояние. Сыпучемерзлые грунты могут вообще не содержать льда, но находятся при отрицательной температуре.
Мерзлые грунты обладают своеобразным строением и сложением, т.е. обладают определенной структурой и текстурой, которые оказывают большое влияние на физико-механические свойства. Грунты с одинаковым составом, но разные по структуре и текстуре могут обладать совершенно различными свойствами. Различают массивную, слоистую и сетчатую текстуры. Массивной текстуре отвечает равномерное распределение льды по объему грунта. При слоистой текстуре включения льда располагаются в виде горизонтальных прослоек. Сетчатая текстура предполагает расположение прослоек льда как в горизонтальном, так и в вертикальном направлении.
Для мерзлых грунтов, так же, как и для талых грунтов, необходимо знать фазовые характеристики. Наряду с общими характеристиками, такими как плотность, которая для мерзлых грунтов обозначается r f, плотность частиц грунта 
, коэффициент пористости мерзлого грунта 
, вводят дополнительные фазовые характеристики. К дополнительным основным фазовым характеристикам относятся: суммарная влажность 
, влажность за счет незамерзшей воды 
, влажность мерзлого грунта, расположенного между ледяными включениями 
.
Суммарная влажность :
, (2.32)
где 
- масса включений льда;
- масса льда-цемента;
- масса незамерзшей воды;
- влажность за счет льда-цемента;
- влажность за счет ледяных включений;
- влажность за счет незамерзшей воды в грунте при данной температуре.
|
|
|
Влажность за счет незамерзшей воды в практических расчетах определяется по формуле:
, (2.33)
где kw - коэффициент, принимаемый в зависимости от вида грунта и его температуры по справочным данным.
Более точно ww можно определить калориметрическим путем, основанном на учете поглощения тепла при оттаивании льда в образце грунта.
Влажность мерзлого грунта, расположенного между ледяными включениями :
. (2.34)
К дополнительным производным фазовым характеристикам для мерзлых грунтов относятся:
Суммарная льдистость 
:
, (2.35)
где 
- объем включений льда и льда-цемента в общем объеме мерзлого грунта 
; r i = 0,9 т/м3 - плотность льда.
Льдистость за счет ледяных включений 
:
. (2.36)
Степень заполнения объема пор мерзлого грунта льдом и незамерзшей водой 
:
. (2.37)
Для мерзлых и оттаивающих грунтов имеют большое значение теплофизические характеристики: теплопроводность λ и объемная теплоемкость C мерзлых и талых грунтов. Эти характеристики определяются опытным путем. Для предварительных расчетов оснований и оснований сооружений II и III классов ответственности допускается принимать эти характеристики по физическим характеристикам по таблицам, приведенным в СНиП 2.02.04-88.
Теплопроводность составляющих грунта изменяется в широких пределах. Для свободной воды она примерно равна 0,5 ккал/м.час.град; для льда – 2 ккал/м.час.град; для минеральной части – от долей до нескольких десятков ккал/м.час.град; для воздуха 0,2…0,3 ккал/м.час.град.
Теплоемкость минерального скелета изменяется от 0,17 кал/г.град для песка до 0,22 кал/г.град для глин. Теплоемкость незамерзшей воды близка к единице, льда – 0,5 кал/г.град. Теплоемкость газообразной составляющей обычно пренебрегают ввиду ее малой величины.
3. Механические свойства грунтов
3.1. Общая характеристика поведения грунта под нагрузкой
Грунт является сложным природным образованием и представляет собой по внутреннему строению дискретную среду. Несвязные, сыпучие грунты состоят из твердых минеральных частиц различной формы и размеров, механически контактирующих между собой в местах соприкосновения. В связных, глинистых грунтах отдельные частицы, кроме того, объединены структурными связями. Как несвязные, так и связные грунты обладают существенной пористостью. Поры грунта полностью или частично могут быть заполнены водой, что также оказывает влияние на сопротивление грунтов внешней нагрузке.
|
|
|
Наблюдаемые при строительстве и эксплуатации инженерных сооружений деформации грунта отличаются значительной величиной, развиваются во времени и, как правило, не исчезают полностью после снятия нагрузки. При деформировании грунтов преимущественно, проявляются свойства пластичности и ползучести. Упругие деформации грунтов также имеют место, но они незначительны и проявляются при специальных режимах нагружения. Упругое деформирование грунтов в области больших давлений, например, в насыпях железных дорог или в основаниях фундаментов машин с динамическими нагрузками, обеспечивается искусственной подготовкой грунтовых массивов к упругому режиму работы.
Деформирование отдельных минеральных зерен, а также сжимаемость поровой воды незначительны и сами по себе не могут приводить к большим деформациям грунта. Основная причина существенных деформаций грунтов заключается в уменьшении его пористости при сжатии, разрушении структурных связей, переукладке и взаимном смещении частиц.
Для количественной оценки возникающих в грунтовых массивах напряжений и деформаций необходимо иметь некоторую идеализированную модель, которая удовлетворительно описывала бы поведение грунта при внешних воздействиях на него, в частности, при механических. Таких моделей в настоящее время разработано достаточно много. Для каждой из них при выполнении практических расчетов необходимо иметь набор расчетных параметров, пригодных для любого напряженного состояния. Такие расчетные параметры называют механическими характеристиками. В простых моделях механические характеристики имеют наглядное физическое истолкование, в более сложных моделях дать ясное физическое истолкование расчетным параметрам не всегда представляется возможным.
Наиболее реальной (с физической точки зрения) является модель грунта, непосредственно описывающая взаимодействие отдельных частиц с учетом структурных связей между ними. Согласно этой дискретной модели зернистая среда моделируется набором контактирующих между собой дисков или шаров различных размеров. Деформирование самих дисков происходит упруго, а нормальные, касательные силы и моменты передаются через точки контактов, вследствие чего между зернами происходит относительное проскальзывание или поворот. На рис. 3.1 показана простейшая расчетная модель дискретной среды, состоящая из набора одинаковых круглых дисков (или шаров).
|
|
|
Рисунок 3.1. - Модель дискретной среды
При решении задач по дискретной теории составляют уравнение равновесия или движения для каждого диска и уравнения, связывающие контактные усилия со смещениями и углами поворота. Для некоторого объема грунта необходимо составить систему линейных алгебраических уравнений и решить ее. Учитывая реальный размер грунтовых частиц, особенно песчаных и глинистых, решение (или даже просто запись) таких систем уравнений на современном этапе развития науки и техники представляется проблематичным. Хотя для таких грунтов, как крупнообломочные, модель дискретной среды может давать хорошие результаты [19].
При решении конкретных задач механики грунтов в большинстве случаев нет необходимости определять контактные усилия между зернами. Эти усилия можно принять непрерывно распределенными по некоторым бесконечно малым площадкам, т.е. определять напряжения на этих площадках так же, как в сплошной среде. При принятии модели сплошной среды все фазы грунта (жидкая, газообразная, твердая) считаются непрерывно распределенными по любому сколь угодно малому элементу или всему объему в целом. Принятие гипотезы непрерывности (гипотезы сплошной среды) позволяет изучать напряженно-деформированное состояние грунтовых массивов с помощью хорошо разработанного аппарата математического анализа для бесконечно малых величин.
Возможность схематизации реальных грунтов в виде модели сплошной среды с физической точки зрения обосновывается тем, что размеры частиц грунта или отдельных структурных элементов во много раз меньше самых малых объемов грунтового массива, подлежащего изучению с точки зрения механики. Например, пылеватые частицы имеют диаметр d < 0,05 мм. В 1 см3 пылеватого грунта содержится более 8 000 000 частиц. Очевидно, что особенности отдельной частицы не будут влиять на свойства всего объема в целом, а для последующего анализа необходимо знать лишь осредненные механические свойства рассматриваемого объема пылеватого грунта.
В трехмерном пространстве напряжения и деформации в точке сплошной среды описываются шестью независимыми компонентами (составляющими). В декартовой системе координат Oxyz напряженное состояние грунта в точке характеризуется нормальными напряжениями 
и касательными напряжениями 
, а деформированное состояние относительными осевыми деформациями 
и относительными сдвиговыми деформациями 
. В механике грунтов принято следующее правило знаков: если внешняя нормаль к площадке совпадает с направлением оси, то положительные направления напряжений противоположны направлению соответствующей оси. На рис. 3.2 показаны положительные направления напряжений, а на рис. 3.3 представлены положительные направления относительных деформаций.
Рисунок 3.2. - Напряжения в сплошной среде.
Рисунок 3.3. - Деформации сплошной среды
В дальнейшем все механические свойства грунтов будут излагаться применительно к различным модификациям только моделей сплошной среды.
3.2. Основные расчетные модели грунта
3.2.1. Модель линейно-деформируемого тела. Принцип линейной деформируемости грунта. Обобщенный закон Гука.
В общем случае относительные деформации зависят от всех компонент напряжений. Вид функций, связывающих деформации с напряжениями, заранее неизвестен, и их можно найти только экспериментальным путем. Эти зависимости называют уравнениями состояния грунта.
Модель линейно-деформируемого тела базируется на использовании линейных зависимостей между относительными деформациями и напряжениями. Применение этой модели к грунтам основано на опытных данных, показывающих, что при малых деформациях в небольшом диапазоне давлений (0,3…0,5 МПа) зависимости между напряжениями и деформациями могут быть приняты линейными. Этот факт формулируется как принцип линейной деформируемости [38]: «при небольших изменениях давлений можно принимать зависимость между общими деформациями и напряжениями для грунтов линейными».
Постоянные коэффициенты, входящие в зависимости деформаций от напряжений, называют деформационными характеристиками. Эти константы характеризуют сам материал и не должны зависеть от выбранной системы координат. В реальных грунтах характеристики деформируемости меняются от точки к точке. Кроме того, деформационные свойства могут отличаться в зависимости от направления. В данном, наиболее общем, случае материал называют неоднородным и анизотропным.
Если же в любой точке грунтового массива деформационные свойства одинаковы и не зависят от направления, то грунт называется однородным и изотропным.
В качестве линейной зависимости между напряжениями и деформациями для изотропных грунтов используется обобщенный закон Гука:
(3.1)
где E — модуль деформации;
n — коэффициент поперечного расширения грунта (коэффициент Пуассона);
G — модуль сдвига, 
.
В этих зависимостях имеется две независимые деформационные характеристики: модуль деформации 
и коэффициент Пуассона 
. Модуль сдвига 
вычисляется в зависимости от и ,т.е. может рассматриваться как производная характеристика. Кроме того, необходимо отметить еще одну производную характеристику - модуль объемной деформации 
, который связывает относительную объемную деформацию со средним напряжением:
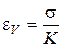, (3.2)
где 
- относительная объемная деформация;
- среднее напряжение.
В отличие от модели линейно-упругого тела, деформации, рассматриваемые в модели линейно-деформируемого тела являются общими, т.е. включают в себя и упругую, и пластическую составляющие. Можно говорить о том, что модель линейно-деформируемого тела с конкретными характеристиками деформируемости предназначена для однократного применения к грунтовой среде. Деформирование грунта неизбежно приводит к изменению его физического состояния - например, пористости и влажности грунта, структурных связей, что влечет за собой изменение его деформационных свойств.
Уравнение состояния (3.1) используется также в дифференциальной форме:
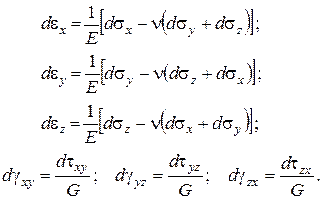(3.3)
Применение модели линейно-деформируемого тела к грунтам позволило решить важные практические задачи определения напряжений и деформаций в основаниях инженерных сооружений, которые будут рассмотрены в главе 4.
3.2.2. Модель жесткопластического тела. Прочность грунта. Закон Кулона и условие прочности Кулона-Мора.
В модели жесткопластического тела рассматриваются два состояния материала - допредельное и предельное. Эти состояния полностью определяются напряжениями, действующими на грунт. Комбинации напряжений 
, при которых материал не разрушается, образуют в шестимерном пространстве напряжений некоторую область, которая называется областью допредельного напряженного состояния. Поверхность, ограничивающая эту область, является геометрическим местом расположения точек пространства, образующих область предельного напряженного состояния. Указанная поверхность характеризует прочность материала и называется поверхностью текучести. Общий вид уравнения поверхности текучести имеет вид:
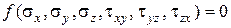. (3.4)
Уравнение (3.4) этой поверхности называют функцией текучести. Функция текучести записывается, как правило, в таком виде, чтобы области допредельного состояния грунта соответствовало неравенство:
. (3.5)
Таким образом, неравенство 
< 0 соответствует напряженному состоянию ниже предела прочности материала, а условие = 0 — пределу его прочности.
Любое напряженное состояние полностью характеризуется тремя главными напряжениями 
, (
). В пространстве главных напряжений наиболее удобно рассмотреть некоторые свойства поверхности текучести для грунтов. Функцию текучести, помимо равенства (3.4), можно выразить через три главных напряжения:
. (3.6)
Рассмотренное определение поверхности текучести имеет место в общем случае пространственного напряженного состояния. Для наглядности приведем пример наиболее простого случая линейного напряженного состояния, широко используемого в Сопротивлении материалов, когда функция текучести (3.4), (3.5) и (3.6) записывается в виде:
,
где s1 - единственное отличное от нуля значение главного нормального напряжения; sт - предел текучести материала при одноосном сжатии или растяжении.
Рассмотрим пространство главных напряжений 
(рис. 3.4), принятых в качестве осей прямоугольной системы координат. В пространстве главных напряжений проведем диагональ, равнонаклоненную к осям главных напряжений. Эта прямая называется гидростатической осью. Точкам, лежащим на гидростатической оси, соответствует равномерное всестороннее обжатие грунта давлением 
. Такое давление называют гидростатическим. Уравнение гидростатической оси имеет вид:
. (3.7)
Опытами установлено, что при гидростатическом сжимающем давлении разрушение грунта не происходит. В то же время, растягивающие напряжения 
приведут к разрушению при некотором значении 
. Поэтому, поверхность текучести будет исходить из точки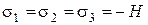 
и иметь гидростатическую ось своей внутренней осью.
Рисунок 3.4. - Поверхность текучести в пространстве главных напряжений
Далее, зафиксируем некоторую точку на гидростатической оси 
и проведем через эту точку плоскость, перпендикулярную гидростатической оси. Эта плоскость называется девиаторной. Уравнение девиаторной плоскости имеет вид:
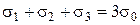. (3.8)
Двигаясь по девиаторной плоскости от центра в любом направлении, на некотором расстоянии от центра будет достигнута точка, которой отвечает предельное напряженное состояние грунта. Геометрическое место этих точек представляет собой некоторую замкнутую линию и является сечением поверхности текучести девиаторной плоскостью. Это сечение увеличивается в размерах при движении девиаторной плоскости вдоль гидростатической оси в положительном направлении. Само сечение будет выпуклым, симметричным относительно главных осей и может представлять собой как замкнутую кривую, так и многоугольник. Конкретный вид поверхности текучести устанавливается по результатам испытания грунта на прочность.
В функцию текучести входят некоторые постоянные. Эти постоянные называют прочностными характеристиками грунта. Закон прочности грунта был установлен Ш. Кулоном в 1773 г. Согласно этому закону, разрушение грунта происходит в виде сдвига. Предельное сопротивление грунта сдвигу выражается в виде предельных касательных напряжений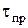 
, действующих по некоторой площадке. Закон Кулона определяет линейную зависимость между предельными касательными напряжениями и нормальными напряжениями 
, действующими по площадке сдвига с нормалью n:
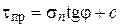. (3.9)
Параметры этой линейной зависимости имеют следующие названия: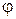 
- угол внутреннего трения грунта (обычно выражается в градусах), 
- удельное сцепление грунта (имеет размерность напряжения).
Параметры 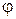и называются характеристиками прочности грунта.
Графическое изображение линейной зависимости (3.9) называют графиком сдвига или прямой Кулона. Уравнение (3.9) и соответствующий график (рис. 3.5) определяют прочность грунта на сдвиг в общем случае, когда сопротивление сдвигу обеспечивается как связностью грунта (
0), так и внутренним трением между частицами (
0). К таким грунтам относится большинство глинистых грунтов, являющихся связными. В некоторых разновидностях глин текучепластичной и текучей консистенции внутреннее трение практически отсутствует (j = 0) и сопротивление сдвигу определяется лишь связностью грунта (жирные глины):
. (3.10)
Такие грунты называются идеально-связными.
Рисунок 3.5. - График сдвига связного грунта
В песчаных грунтах сопротивление сдвигу формируется преимущественно за счет внутреннего трения между частицами (
). Закон прочности для песков обычно записывается в виде:
. (3.11)
|
|
|
