Выражение (2.27) можно записать в виде 6 глава

 

4.3.2. Определяющие уравнения. Уравнение совместности

 

Плоская задача в декартовой системе координат. Уравнение совместности. Исходная система уравнений плоской задачи в декартовых координатах, как было показано в предыдущем параграфе, включает восемь уравнений. Естественно попытаться ввести некоторые упрощения.

Прежде всего, исключим перемещения u и w из выражений (4.17). Продифференцируем первое из них дважды по z, второе дважды по x, третье сначала по x, потом по z:

, , .

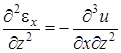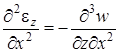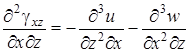Сравнивая полученные выражения, имеем

.

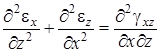(4.21)

Это уравнение называется уравнением совместности или уравнением неразрывности деформаций. Физический смысл уравнения совместности заключается в том, что оно обеспечивает сохранение сплошности среды после деформирования.

Это уравнение следует объединить с уравнениями равновесия (4.15) в общую систему. Однако прежде надо преобразовать (4.21) к напряжениям. С этой целью подставим в него выражения закона Гука (4.16), предварительно взяв необходимые производные

, , .

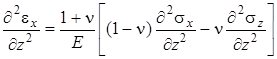В результате имеем

.

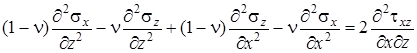(4.22)

Найденное уравнение можно преобразовать к более компактной форме с помощью уравнений равновесия (4.14). С этой целью продифференцируем первое из уравнений (4.14) по x, а второе - по z и сложим:

.

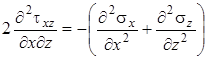Подставив это равенство в правую часть уравнения (4.22), после приведения подобных членов и сокращения на общий множитель (1 - n) получим искомое уравнение совместности в прямоугольной системе координат, выраженное через напряжения:

.

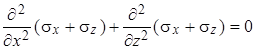(4.23)

Часто это уравнение записывают с помощью оператора Лапласа 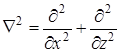, тогда оно принимает более компактный вид:

.

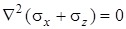(4.24)

Последнее равенство вместе с уравнениями равновесия составляют определяющую для плоской задачи систему из трех уравнений - два уравнения равновесия и уравнение совместности - с тремя неизвестными функциями напряжений, отыскание которых дает искомое решение плоской задачи:

, , .

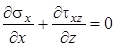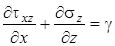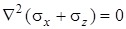(4.25)

Можно пойти дальше по пути упрощений. Введем некоторую функцию j (здесь j - не угол внутреннего трения (!)), связанную с напряжениями следующим образом

, , .

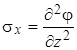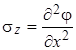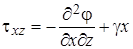(4.26)

Функция j называется функцией напряжений или функцией Эри. Нетрудно убедиться, что при подстановке выражений (4.26) в уравнения равновесия (4.15) получаются тождества. Функция напряжений, таким образом, позволяет свести определяющую систему плоской задачи (4.25) к одному уравнению:

,

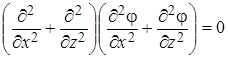(4.27)

или в компактной форме

.

(4.28)

В результате плоская задача определения напряженно-деформированного состояния грунтовой среды будет сводиться к решению только одного дифференциального уравнения, содержащего одну неизвестную функцию, которая должна удовлетворять этому уравнению и граничным условиям.

Плоская задача в полярной системе координат. Некоторые задачи удобно решать в полярной системе координат Or q. В такой системе координат уравнения равновесия бесконечно малого элемента, показанного на рис. 4.8, имеют вид:

 

 

Рисунок 4.8. - Схема напряженного состояния в точке (плоская задача, полярные

координаты)

 

, .

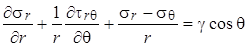(4.29)

Известно, что сумма нормальных напряжений по двум взаимно перпендикулярным площадкам - величина инвариантная, т.е. не зависящая от выбранной системы координат. Поэтому справедливы равенства

.

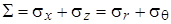(4.30)

Используя эту величину, а также известные соотношения между декартовыми и полярными координатами 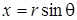, , 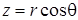уравнение совместности (4.23) или (4.24) можно преобразовать к полярной системе координат:

.

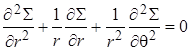(4.31)

Окончательно определяющая система уравнений плоской задачи в полярных координатах r q примет вид

, , .

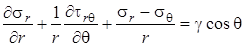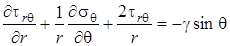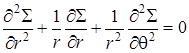(4.32)

Если пренебречь собственным весом среды (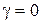), можно ввести функцию напряжений посредством соотношений

, , .

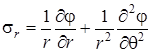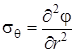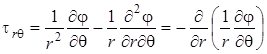(4.33)

Тогда уравнение совместности, аналогичное (4.27) и (4.28), запишется в виде

.

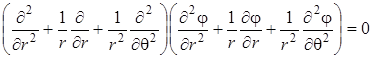(4.34)

или

,

где .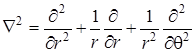

Пространственная задача в декартовой системе координат. При решении пространственной задачи в напряжениях приходится сталкиваться с наиболее сложной ситуацией, на которой остановимся лишь коротко.

В рассматриваемом случае необходимо подобрать шесть функций для компонент напряжений, удовлетворяющих помимо уравнений равновесия (4.18) и граничных условий шести уравнениям совместности [2]

, , , , , ,

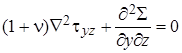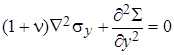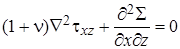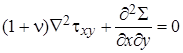(4.35)

где , .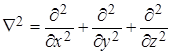

Осесимметричная задача в цилиндрической системе координат. Особый интерес представляет случай осевой симметрии. Схема осесимметричного напряженного состояния в точке в цилиндрической системе координат Orz q показана на рис. 4.9 (ось Oz направлена вертикально вниз). Уравнения равновесия для этого случая имеют вид:

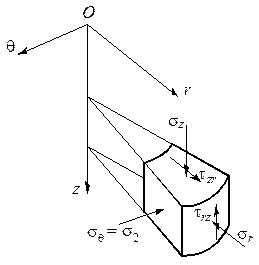
Рисунок 4.9. - Схема напряженного состояния в точке (осесимметричная задача,

цилиндрические координаты)

 

, .

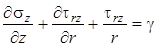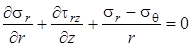(4.36)

Запишем уравнения совместности, опуская их вывод. При данном виде напряженного состояния таких уравнений четыре:

; ; ; ,

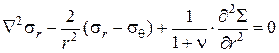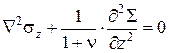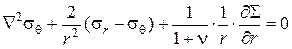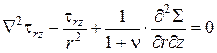(4.37)

где .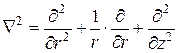

Функции Эри, связанная с напряжениями равенствами

, ,

, ,

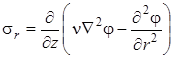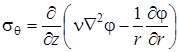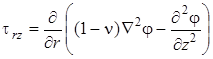(4.38)

должна удовлетворять уравнению

,

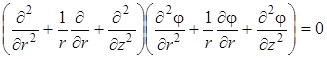(4.39)

или короче

,

где .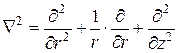

 

4.3.3. О методах решения задач теории линейно-деформируемой среды

 

Главная трудность при решении рассмотренных в п. 4.3.2 задач состоит в подборе такой функции напряжений, которая помимо уравнений (4.28), (4.34) или (4.39), удовлетворяла бы и граничным условиям. Можно задаться каким-либо определенным видом функции с некоторыми постоянными коэффициентами, исходя из физической сути задачи, граничных условий или других дополнительных соображений. Например, в известной в теории упругости задаче о силе, приложенной внутри упругого пространства функция Эри не должна содержать линейных размеров, поскольку их нет в самой задаче; в задаче о вертикальной силе, приложенной к полупространству (см. ниже задачу Буссинеска) ясно, что с глубиной напряжения должны уменьшаться и т.д.

Как только удается в конкретной задаче подобрать функцию Эри, то по соответствующим формулам нетрудно определить все компоненты напряжений, деформаций и перемещений в любой точке рассматриваемой области. Так, в плоской задаче для этого следует использовать зависимости (4.15)…(4.17).

В замкнутом виде получить эту функцию далеко не всегда возможно, и при решении приведенных выше уравнений широко используют метод конечных разностей. Если заменить частные производные в (4.28), (4.34) или (4.39) отношениями конечных приращений, то получим систему линейных алгебраических уравнений.

Другие подходы, также заключающиеся в применении численных решений, реализуются методом конечных элементов и методом граничных интегральных уравнений, которые получили значительное развитие в последние десятилетия. В МКЭ исследуемая область разбивается на отдельные конечные элементы, в пределах каждого из которых устанавливается связь между усилиями и перемещениями, а затем, используя вариационные принципы, для всех элементов составляется и решается общая алгебраическая система уравнений. В методе граничных интегральных уравнений искомые функции определены на границе области, и задача сводится к решению интегральных уравнений. Подробное описание методов аналитических и численных решений можно найти в специальной литературе.

Ниже мы будем останавливаться преимущественно на классических решениях базовых плоских и пространственных задач ТЛДС, полученных в замкнутом виде, и являющихся наиболее важными с практической точки зрения, результаты которых лежат в основе многих инженерных методов и расчетов.

 

4.3.4. Понятие о бытовых и дополнительных напряжениях

 

В инженерной практике при решении задач о напряженно-деформированном состоянии основания принято отдельно определять напряженное состояние, возникающее от собственного веса грунта и от внешних нагрузок. Такой подход вполне оправдан, поскольку в ТЛДС, как отмечалось, справедлив принцип суперпозиции. В соответствии со сказанным, введем понятия бытовых и дополнительных напряжений.

Бытовые напряжения - это напряжения, возникающие в основании от действия собственного веса грунта - веса вышележащих слоев. Обозначаются индексом «g», например, s _zg.

Дополнительные напряжения - это напряжения, возникающие только от действия внешней нагрузки. Обозначаются индексом «p», например, s _zp.

Полное напряженное состояние находится суммированием решений:

, ,

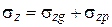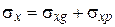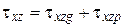
и т.д.

В дальнейшем при раздельном анализе бытового и дополнительного напряженного состояния индексы «g» и «p» будем, как правило, опускать.

Определение бытового напряженного состояния, вообще говоря, является крайне сложной задачей, поскольку для этого необходимо знать всю историю осадконакопления на территории каждой конкретной строительной площадки [30]. При этом может оказаться, что принцип линейной деформируемости будет вообще неприменим. Вместе с тем, на практике бытовые напряжения рассчитываются весьма просто вследствие обычно принимаемых дополнительных гипотез об упрощенном характере процесса осадконакопления (см. п. 4.4). Принято считать, что точности таких расчетов в большинстве случаев достаточно для инженерных целей. В результате основное внимание уделяют определению дополнительных напряжений, где особенно сложен поиск решений в замкнутом виде.

Итак, с точки зрения строгой постановки ТЛДС применение данной методики определения полных напряжений вполне корректно. Вместе с тем, этот прием используется и в приближенных расчетах. Например, учет неоднородности основания, который для бытового напряженного состояния в рамках обычно принимаемых допущений не представляет трудностей, при определении дополнительных напряжений выполняется сравнительно редко. Однако полученные в результате напряжения также суммируются, что для практических расчетов часто оказывается оправданным.

 

 

4.4 Задача о природном напряженном состоянии основания

 

Однородное основание. Рассмотрим простейший случай определения бытового напряженного состояния однородного изотропного линейно-деформируемого полупространства, ограниченного сверху горизонтальной плоскостью (рис. 4.10, а). Для большей общности положим, что на всей поверхности основания действует равномерно распределенное давление интенсивностью q. Возьмем прямоугольную систему координат, оси Oх и Oу которой расположены на поверхности основания, а ось Oz направим вертикально вниз. Поскольку в направлении осей Ox и Oy на поверхности основания ничего не изменяется, то, очевидно, напряжения в основании не зависят от координат х и у. 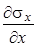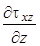В таком случае в дифференциальных уравнениях равновесия системы (4.15) частные производные и равны нулю. Более того, так как касательные силы на поверхности основания отсутствуют, то можно ожидать, что касательные напряжения t _xz отсутствуют и внутри основания. Согласно сказанному, напряжения s _x, s _z могут зависеть только от одной координаты z. Поэтому частную производную 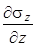в уравнении равновесия следует заменить на простую производную 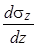. В результате от двух уравнений равновесия остается одно простое уравнение

 

 

 

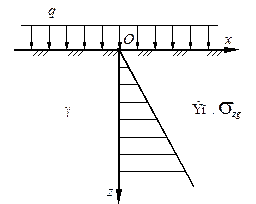
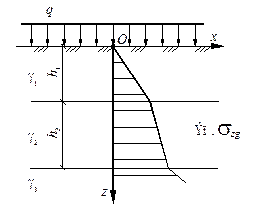
Рисунок 4.10. - Схемы к определению бытовых напряжений: (а) в однородном основании; (б) в слоистом основании

 

.

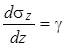(4.40)

Интегрируя его, получим

,

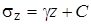(4.41)

где С - произвольная постоянная интегрирования.

Константу С определим из граничного условия на поверхности основания. Так как при z = 0, s _z = q, то С = q, и окончательно имеем

.

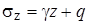(4.42)

Таким образом, в однородном основании напряжение s _z нарастает с глубиной по линейному закону (рис. 4.10, а).

Поскольку t _xz = 0, то напряжение s _z является главным напряжением и, очевидно, наибольшим, так что s _z = s₁. Помимо напряжения s _z, для полноты картины надо отметить еще и боковые напряжения s _x, s _y. Эти напряжения установим, полагая, что деформации основания в процессе его геологического формирования происходили равномерно в направлении оси Oz, и в последующем оно не подвергалось тектоническим процессам (в других случаях определения бытовых напряжений также будем придерживаться этой гипотезы). При таких предположениях деформации основания под действием только собственного веса грунта происходили в условиях невозможности боковых деформаций e _x = e _y = 0. Иначе говоря, деформирование совершилось в условиях компрессионного сжатия в направлении оси Oz. В таком случае боковые напряжения определяются зависимостями

,

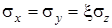(4.43)

где 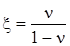- коэффициент бокового давления в условиях компрессионного сжатия.

Ясно, что эти напряжения также являются главными, так что 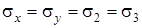, а их эпюры качественно повторяют эпюру s _z, но имеют меньшие в x раз ординаты.

Третье уравнение определяющей системы (4.25) очевидно удовлетворяется, так как вторые производные от 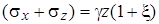по х и z равны нулю. Таким образом, полученное решение удовлетворяет всем уравнениям определяющей системы (4.25).

Отметим, что если отказаться от принятых допущений, то напряжения s _х, s _у окажутся неопределенными.

Основание с горизонтальным напластованием грунтов. Перейдем к случаю, когда в основании возможно выделить несколько инженерно-геологических элементов, залегающих горизонтально (рис. 4.10, б). Опустим выводы формул, они аналогичны только что рассмотренным. Большинство приведенных выше рассуждений также остается справедливым и в этом случае.

Запишем формулу для вертикального бытового напряжения, возникающего на глубине 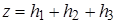(рис. 4.10, б):

.

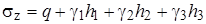В общем случае для точки с координатой z, находящейся в n -м от поверхности слое эта формула примет вид:

,

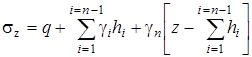В этих формулах: z - координата точки, в которой определяется напряжение, n - общее количество слоев, причем рассматриваемая точка находится в n -м слое; g _i и h_i - удельный вес и мощность i -го слоя.

В произвольном i -м слое остальные напряжения определятся как

, ,

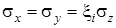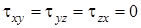где 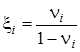- коэффициент бокового давления i -го слоя, n _i - коэффициент Пуассона i -го слоя.

Эпюра вертикальных напряжений s _z дана на (рис. 4.10, б).

Однородное обводненное основание. Если основание обводнено (рис. 4.11, а), и вода свободно перемещается по порам грунта, то по закону Архимеда она оказывает взвешивающее действие на частицы грунта. Тогда для однородного обводненного основания напряжения на глубине z с учетом сказанного равны:

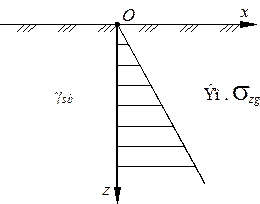
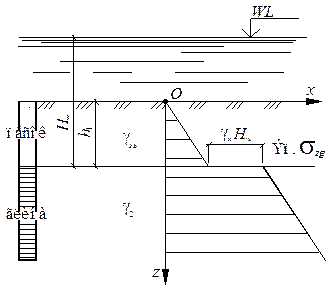
Рисунок 4.11. - Схемы к определению бытовых напряжений: (а) в однородном

обводненном основании; (б) в двухслойном обводненном основании

 

 

, , .

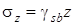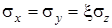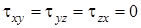где 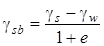- удельный вес грунта с учетом взвешивания водой, g _s - удельный вес частиц грунта, g _w» 10 кН/м³ - удельный вес воды, e - коэффициент пористости.

Степень взвешивания частиц грунта при его обводнении для разных видов грунтов будет различна [35]. Считается, что чем меньше общая площадь контактов между частицами, тем полнее проявляется взвешивание для каждой из них. Дело в том, что по площадям контактов между частицами гидростатическое давление воды не может передаваться. В этом случае имеет место, как говорят, неполное взвешивание частиц. Принято считать, что полному взвешиванию подвергаются пески и супеси, несколько хуже суглинки, а для плотных глин взвешивания может вообще не быть.

Двухслойное обводненное основание. Рассмотрим обводненное основание, например, в русле реки. Допустим, что с поверхности залегает водопроницаемый песчаный грунт, а подстилает его слой плотной глины (рис. 4.11, б). Этот слой можно считать водоупорным. Такая ситуация может встречаться в транспортном строительстве, в частности при сооружении мостовых переходов.

Итак, в песчаном слое в уровне его подошвы согласно вышесказанному вертикальные бытовые напряжения с учетом взвешивания водой составят

,

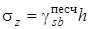где 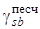- удельный вес песчаного грунта с учетом взвешивания водой, h - мощность его слоя.

Переходя в слой глины, очевидно, выталкивающая сила исчезает. Кроме того, глина будет воспринимать дополнительное давление от веса столба воды высотой H_w (рис. 4.11, б). Это давление компенсировалось в первом слое за счет всестороннего обжатия водой каждой частицы песка, т.е. гидростатического давления. В результате на границе слоев песка и глины в эпюре вертикальных напряжений возникает скачок, равный давлению от столба воды 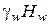. Окончательно эпюра бытовых вертикальных напряжений примет такой вид, как показано на (рис. 4.11, б), а компоненты бытовых напряжений определятся зависимостями:

, , ,

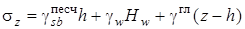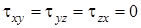где 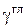- удельный вес глины, x - коэффициент бокового давления для соответствующего слоя.

 

4.5. Плоская задача определения напряжений от внешних нагрузок

 

4.5.1. Задача о погонной нагрузке (задача Фламана, 1892 г.)

 

Задача Фламана имеет фундаментальное значение, поскольку, как будет показано далее, оно позволяет решать разнообразные задачи о напряженно-деформированном состоянии основания в условиях плоской деформации.

Рассматриваемая задача состоит в следующем. Вдоль некоторой прямой, проведенной на поверхности основания, нормально к поверхности действует равномерно распределенная сосредоточенная погонная нагрузка p (рис. 4.12). Остальная часть поверхности основания остается свободной. Требуется определить напряженно-деформированное состояние основания от такой нагрузки. При этом в уравнениях равновесия надо полагать g = 0, поскольку будут определяться дополнительные напряжения.

Рисунок 4.12. - Напряженное состояние элемента основании в задаче Фламана

 

Переходя к решению задачи, предположим, что при указанных условиях загружения в основании возникает простое радиальное напряженное состояние, в котором s _r - наибольшее главное напряжение s₁, а наименьшее главное напряжение s_q º 0 и, следовательно, t _{r q} º 0 (см. рис. 4.12). Принятое предположение будет оправдано в ходе решения. Сейчас же отметим, что оно удовлетворяет граничным условиям задачи, так как равенство s_q º 0 означает отсутствие давления на поверхности основания, разумеется, за исключением точек оси Oу, где действует нагрузка p. Согласно этому предположению второе из уравнений системы (4.32) тождественно обращается в нуль, а первое уравнение принимает более простой вид:

.

Разделим в нем переменные

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: