Выражение (2.27) можно записать в виде 3 глава

 

Таблица 3.1. - Значения коэффициента Пуассона

Вид грунта	Коэффициент Пуассона n
Крупнообломочный	0,27
Пески, супеси	0,30
Суглинки	0,35
Глины	0,42

 

Другая форма представления результатов компрессионных испытаний заключается в определении зависимости коэффициента пористости от напряжения 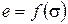. Такая зависимость устанавливается из предположения, что деформации образца грунта происходят исключительно за счет уплотнения, т.е. уменьшения объема пор при неизменном объеме скелета грунта. График этой зависимости (рис. 3.15) также называется компрессионной кривой. Поскольку в основном сжатие грунта происходит за счет уменьшения пористости, то компрессионная кривая 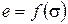наглядно показывает природу явления. Отметим, что в зависимости от целей, которые ставятся при компрессионных испытаниях, может потребоваться либо та, либо другая обработка результатов.

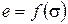Рассмотрим переход от зависимости к зависимости . Для этого установим связь между коэффициентом пористости и относительной деформацией. Пусть образец грунта площадью A и высотой h имеет некоторую начальную пористость, характеризуемую коэффициентом пористости 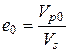, (V_{p 0} - начальный объем пор, 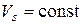- объем скелета грунта). Значение e_i, соответствующее некоторому давлению s _i и осадке образца s_i будет равно:

,

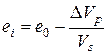где 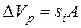- изменение объема пор.

Окончательно, получим выражение:

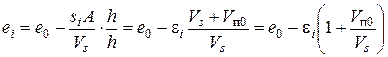
или

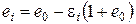, (3.44)

С помощью этой зависимости строим компрессионную кривую 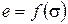(рис. 3.15). В общем случае на компрессионной кривой (линия 1) можно выделить два участка. На первом участке s < s_стр деформации грунта малы, так как при таких напряжениях работают жесткие структурные связи. При увеличении напряжений s > s_стр (на втором участке) структурные связи разрушаются и грунт начинает сильно уплотняться, т.е. коэффициент пористости сильно меняется. Величина s_стр называется структурной прочностью грунта. Для грунтов, не имеющих жестких структурных связей, первый участок отсутствует (кривая 2 на рис. 3.15).

По компрессионной кривой также можно оценить сжимаемость грунта. Она оценивается коэффициентом сжимаемости в определенных интервалах давления (см. рис. 3.15):

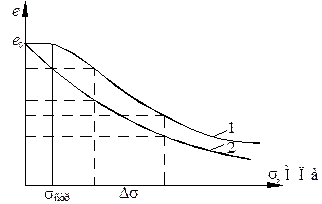
Рисунок 3.15. - Компрессионная кривая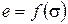

 

 

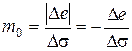(3.45)

Из рис. 3.15 видно, что чем круче компрессионная кривая, тем сжимаемость выше. Очевидно также, что в разных интервалах давления сжимаемость различная. Запишем уравнение (3.45) в дифференциальной форме:

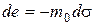(3.46)

Это уравнение называют дифференциальным законом уплотнения грунта.

Коэффициент относительной сжимаемости 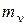связан с коэффициентом сжимаемости 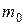согласно (3.38) и (3.45), а также учитывая, что 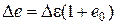, следующим соотношением:

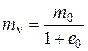. (3.47)

Поэтому, используя компрессионную кривую, можно выразить модуль деформации через коэффициент сжимаемости:

. (3.48)

Приведем еще один вид записи уравнения компрессионной кривой, позволяющий рассматривать изменение коэффициента пористости при напряжениях, больших природного давления , действовавшего на образец грунта [37]:

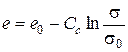, (3.49)

где e ₀ - начальный коэффициент пористости; C_c - коэффициент компрессии; s₀ - напряжение, соответствующее начальному коэффициенту пористости грунта.

Рассмотрим теперь поведение грунта в компрессионных условиях при разгрузке. После нагружения (кривая 1 на рис. 3.16), будем постепенно разгружать образец грунта в компрессионном приборе (кривая 2, рис. 3.16). Образец будет увеличиваться в объеме, его коэффициент пористости будет возрастать. Зависимость изменения коэффициента пористости от давления при разгрузке называют кривой декомпрессии. После разгрузки будем вновь нагружать образец (кривая 3, рис. 3.16). Пористость его при этом будет уменьшаться, и мы получим кривую повторной компрессии.

 

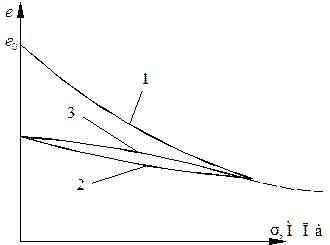
Рисунок 3.16. - Кривые компрессии и декомпрессии

 

Такие циклы нагрузки-разгрузки можно повторять многократно. Анализируя характер деформирования образца, можно сделать следующие выводы [8]:

1. При цикле «нагрузка-разгрузка» грунт получает остаточную деформацию.

2. Повторная компрессия образует с кривой декомпрессии петлю гистерезиса.

3. Повторные ветви компрессии стремятся выйти на траекторию кривой компрессии.

4. На кривой повторной компрессии имеется перегиб в точке, соответствующей максимальному давлению при предыдущем цикле «нагрузка-разгрузка». Таким образом, точка перегиба на компрессионной кривой позволяет определить давление, до которого был загружен грунт. Максимальное давление, когда-либо обжимавшее грунт, называют историческим. Давление, действующее в настоящее время на данной глубине, называют природным, или бытовым. Грунты, у которых историческое давление больше природного, называют переуплотненными, если историческое давление равно природному, грунты называют нормально уплотненными.

5. При многократном повторении циклов нагружения и разгружения остаточные деформации постепенно убывают и грунт начинает деформироваться упруго.

3.4. Сдвиговые испытания грунтов. Определение прочностных характеристик

 

Прочность грунта характеризуется его сопротивлением сдвигу. Для изучения предельного сопротивления грунтов сдвигу разработаны специальные приборы и методики испытаний. Наиболее распространенными в настоящее время являются сдвиговые приборы.

Существует много конструктивных разновидностей сдвиговых приборов, среди которых можно выделить две группы:

- приборы со ступенчатым загружением (рис. 3.17);

- приборы с непрерывным загружением (рис. 3.18).

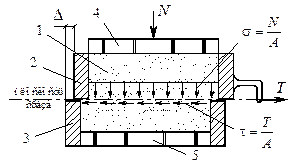
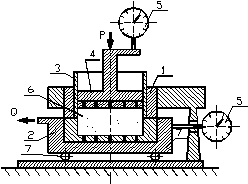
Рисунок 3.17. - Принципиальная схема сдвиговых испытаний (а) и конструкция сдвигового прибора ступенчатого нагружения (б)

Обозначения на схеме (а): 1 - грунт, 2 - подвижная часть корпуса, 3 - неподвижная часть корпуса, 4 - пористый поршень, 5 - пористое дно. Обозначения на схеме (б): 1 - неподвижная часть корпуса, 2 - подвижная часть (коретка), 3 - кольцо, 4 - штамп, 5 - индикаторы, 6 - грунт, 7 - ролики

Рисунок 3.18. - Конструкция сдвигового прибора непрерывного нагружения: 1,2 - винтовые домкраты, 3,4 - динамометры, 5,6,12 - индикаторы (мессуры), 7 - пористый штамп, 8 - грунт, 9 - неподвижная обойма (каретка), 10 - подвижная обойма (каретка), 11 - станина

Рассмотрим кратко методику испытаний на приборах обоих типов. Испытанию подвергаются образцы грунта ненарушенной структуры, иногда - нарушенной структуры с заданными исходными значениями плотности и влажности (например, для песков).

Сдвиговой прибор ступенчатого нагружения изображен на рис.3.17. Образец грунта помещается в металлическое кольцо, разделенное на части - подвижную и неподвижную обоймы. Подвижной может быть как нижняя, так и верхняя обойма. Между обоймами до проведения опыта устанавливается небольшой зазор, который необходимо сохранять в течение всего опыта. Таким образом, создается фиксированная плоскость, по которой произойдет срез подвижной части грунта относительно неподвижной. Вертикальное нормальное напряжение в плоскости сдвига создается с помощью рычажной системы в предположении, что нормальные напряжения в плоскости сдвига распределены равномерно, т.е. равны вертикальной приложенной силе, деленной на площадь образца. Нормальное напряжение сохраняется в течение всего опыта постоянным. Образец грунта до приложения сдвигающей силы обжимается некоторое время, зависящее от вида грунта, нормальным напряжением s.

Пусть в отдельном данном опыте 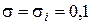МПа. Будем теперь к подвижной обойме отдельными ступенями прикладывать сдвигающую силу Т через соответствующую рычажную систему. Считается, что касательные напряжения при любой ступени нагружения также распределены в плоскости сдвига равномерно. Под действием приложенной ступени горизонтальной сдвигающей силы подвижная часть грунта начнет перемещаться относительно неподвижной. За величиной перемещений наблюдают с помощью специальных измерителей, например, индикаторов часового типа. Если сила Т мала, то перемещения одной части образца относительно другой будут затухающими, и непрерывного сдвига одной части образца относительно другой не произойдет, т.е. прочность грунта при данном соотношении нормальных и касательных напряжений исчерпана не будет. Будем ступенями увеличивать силу Т до тех пор, пока не произойдет срез образца. За момент среза обычно принимают такое состояние образца, когда при неизменной горизонтальной силе скорость перемещения одной части образца относительно другой нарастает. Предельное значение касательного напряжения, при котором наступает непрерывный сдвиг, называют сопротивлением грунта сдвигу. Опыты показывают, что сопротивление грунта сдвигу зависит от величины нормального напряжения, действующего в плоскости сдвига. Чтобы получить сопротивление сдвигу при другом нормальном напряжении, нужно провести другой опыт с образцом грунта, имеющим те же исходные физические характеристики. Поскольку нам хотелось бы знать величину предельного касательного напряжения 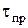при любом значении нормального напряжения, с помощью экспериментов необходимо установить функциональную зависимость .

Теперь кратко рассмотрим методику испытания на приборе непрерывного загружения, изображенного на рис. 3.18. С помощью домкрата 1 задается нормальное вертикальное давление, в течение всего опыта оно поддерживается постоянным. До начала опыта между подвижной и неподвижной обоймами устанавливается зазор в плоскости сдвига. Домкратом 2 создают непрерывную сдвигающую нагрузку. Если грунт сопротивляется сдвигу, то показания динамометра при домкрате 2 будут возрастать. При достижении сдвигающей силы предельного значения рост показаний динамометра прекращается. Динамометры заранее тарируются, т.е. в зависимости от показания индикатора деформаций получают действующее усилие. В результате проведения одного опыта мы получим пару значений величин s _i и t _i, при которых произойдет разрушение грунта.

Для определения прочностных характеристик грунта проводят серию опытов при различных вертикальных давлениях на образец грунта. Количество опытов должно быть достаточным для статистической обработки результатов. Графическое изображение результатов сдвиговых испытаний в координатах s, t_пр показано на рис. 3.19, а. На рис. 3.19, б показан график зависимости перемещений по площадке сдвига от величины касательного усилия при его возрастании. Результаты испытаний обычно описываются законом Кулона (3.9):

.

 

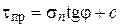Рисунок 3.19. - Результаты сдвиговых испытаний: (а) - опытные точки зависимости предельных касательных напряжений от нормального давления и их линейная аппроксимация, (б) - зависимость деформаций при сдвиге от касательного напряжения

 

Численные значения параметров прочности грунта j и c для опытов находят методом наименьших квадратов:

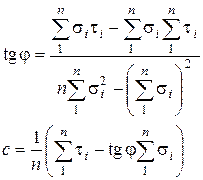(3.50)

 

Эти значения параметров прочности определяют прямую Кулона, наилучшим образом соответствующую опытным данным.

 

3.5. Ползучесть глинистых грунтов при сдвиге. Мгновенная и длительная прочность грунта

 

Рассмотрим процесс ползучести глинистого грунта при сдвиге на примере испытания грунта в приборе одноплоскостного среза. Проведем серию опытов образцов одного и того же глинистого грунта. Опыты проводятся при одинаковых нормальных напряжениях s и различных касательных напряжениях t _i. При этом касательные напряжения прикладываются к образцу грунта сразу, за одну ступень.

Горизонтальное смещение верхнего кольца D при сдвиге можно фиксировать с помощью индикатора часового типа. Таким образом, после приложения горизонтальной сдвигающей силы, характеризуемой напряжением t _i можно наблюдать развитие сдвиговых деформаций во времени - , т.е. процесс ползучести. Если при некотором значении сдвигающего напряжения t₅ не происходит разрушения грунта, то имеет место процесс затухающей ползучести (рис. 3.20, а). Увеличивая значение сдвигающих напряжений в других опытах 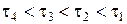, будем добиваться разрушения грунта в некоторые моменты времени t _{р, i}. Очевидно, что чем больше значение сдвигающей нагрузки, тем быстрее разрушится грунт, т.е. t _р,1 < t _р,2 < t _р,3 < t _р,4 (рис. 3.20, а).

 

 

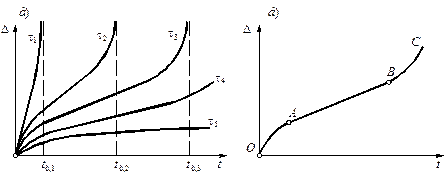
Рисунок 3.20. - Ползучесть глинистых грунтов при сдвиге: (а) - при различной величине сдвигающего усилия (t₁ > t₂ > t₃ > t₄ > t₅), (б) - кривая ползучести: OA - неустановившаяся ползучесть, AB - неустановившаяся ползучесть, BC - прогрессирующее разрушение.

 

 

На кривой ползучести выделяют три участка (рис. 3.20, б): неустановившаяся ползучесть - участок ОА, установившаяся ползучесть - участок АВ, и прогрессирующее разрушение - участок ВС. Наибольший интерес представляют участки установившейся ползучести и прогрессирующего разрушения.

При установившейся ползучести скорость деформирования уменьшается, достигая некоторой постоянной величины . С этой постоянной скоростью грунт деформируется на участке установившейся ползучести. Далее, на участке прогрессирующего разрушения, скорость деформирования увеличивается и приводит к разрушению грунта. В рассмотренном опыте, начиная с некоторого достаточно большого значения t₁ касательного напряжения кривая ползучести имеет только один участок - прогрессирующее разрушение.

Итак, в некотором диапазоне касательных напряжений t _i соответствующие кривые ползучести отражают указанные стадии деформирования и каждому касательному напряжению отвечает определенное время до разрушения образца t _{р, i}. По результатам этих опытов строится кривая зависимости времени разрушения от касательного напряжения. Вид кривой показан на рис. 3.21. По этому графику можно найти максимальное касательное напряжение, не вызывающее разрушение грунта - 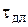и минимальное касательное напряжение, вызывающее практически мгновенное разрушение грунта - 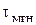(т.е. на кривой ползучести выделяется только участок прогрессирующего разрушения).

 

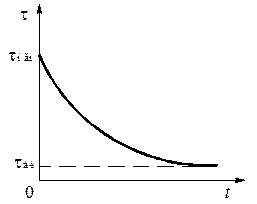
Рисунок 3.21. - Мгновенная и длительная прочность грунта на сдвиг

 

Параметр 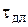называется длительной прочностью грунта на сдвиг, величина 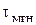- мгновенной прочностью грунта на сдвиг. Выполняя подобные серии опытов для различных нормальных давлений можно получить зависимости предельного касательного напряжения от нормального давления как длительной, так и для мгновенной прочности грунта:

(3.51)

Величины являются параметрами длительной прочности грунта на сдвиг, а величины 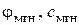- параметрами мгновенной прочности.

 

3.6. Стабилометрические испытания грунтов. Определение механических характеристик грунта

 

Рассмотренные ранее компрессионные и сдвиговые приборы для определения характеристик деформируемости и прочности имеют ряд существенных недостатков. Перечислим некоторые из них.

1. При проведении сдвиговых испытаний контролируемыми величинами являются суммарная вертикальная сила, приложенная к верхней грани образца, и суммарная сдвигающая сила. Напряженное же состояние непосредственно в плоскости сдвига неопределенно и оценивается приближенно. Между стенками прибора и грунтом практически всегда есть трение, поэтому распределение нормального давления по плоскости сдвига неравномерно. Это трение не учитывается ни в сдвиговых, ни в компрессионных испытаниях. Более того, неизвестно даже суммарное усилие в плоскости сдвига, если сила трения не учитывается путем непосредственного измерения с помощью дополнительных довольно сложных устройств, которых в стандартных приборах нет.

2. Площадь образца при сдвиге не остается постоянной по мере смещения подвижной обоймы относительно неподвижной.

3. Необходимость создания зазора между обоймами приводит к появлению ряда погрешностей, иногда весьма существенных. Например, при испытании грунтов текучей консистенции происходит выжимание грунта через зазор, а влажность при этом может сильно меняться. Величину зазора в стандартных приборах ступенчатого загружения в процессе самого опыта регулировать весьма затруднительно.

4. Результаты сдвиговых испытаний можно использовать непосредственно лишь применительно к теории прочности Мора-Кулона, которая не учитывает влияния на прочность промежуточного главного напряжения 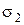. При сдвиговых испытаниях такой учет невозможен, поскольку 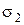неизвестно.

Аналогичных недостатков в сдвиговом и компрессионных приборах довольно много, и они детально анализируются в специальной литературе. Многих из них удается избежать, исследуя прочность и деформируемость грунтов в более совершенных приборах - стабилометрах или приборах трехосного сжатия.

В настоящее время разработано много модификаций приборов трехосного сжатия. Детальный обзор конструкций стабилометров и методик работы на них дается, например, в [4].

Наиболее совершенными в настоящее время являются стабилометры, позволяющие испытывать образцы кубической формы, к каждой грани которых можно прикладывать независимо друг от друга нормальные напряжения и регулировать величину любого напряжения по заданному закону. Нормальные напряжения, прикладываемые к граням образца, обычно считают главными. Поэтому такие приборы называют приборами с независимо управляемыми главными напряжениями и деформациями.

За рубежом широко применяются стабилометры, в которых исследуются образцы грунта в виде полых цилиндров. Изменение главных напряжений в этих приборах создается путем независимого изменения внутреннего и внешнего давлений в цилиндрическом полом образце и осевого давления по торцам. Модификацией стабилометров такого типа являются приборы, позволяющие создавать деформацию кручения образца.

Приборы двух этих типов довольно сложны в изготовлении и в настоящее время используются в основном для исследовательских целей, поэтому методику испытаний на них мы опускаем.

В производственной практике нашли применение более простые по конструкции стабилометры, в которых два главных напряжения одинаковы. На рис. 3.22 показаны принципиальная схема нагружения образца цилиндрической формы.

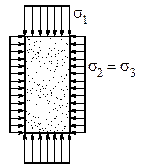
Рисунок 3.22. - Напряженное состояние грунта в стабилометре

 

По торцам на образец действует вертикальное давление , а с боков он обжимается давлением . Конструктивных оформлений стабилометров очень много. Ограничимся схемой, приводимой в ГОСТ 26518-85 (рис. 3.23).

 

 

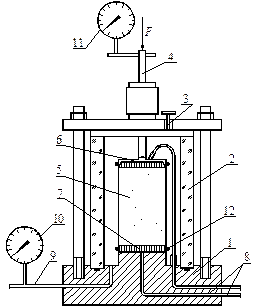
Рисунок 3.23. - Конструкция стабилометра: 1 - жесткое основание, 2 - рабочий корпус камеры, 3 - вентиль для выпуска воздуха, 4 - корпус штока, 5 - грунт, 6 - верхний пористый штамп, 7 - нижний пористый штамп, 8 - трубки для тока воды из образца и измерения давления в пористой воде, 9 - трубка для заполнения камеры водой измерения в ней давления, 10 - манометр, 11 - индикатор перемещений, 12 - уплотнитель

 

На жесткое основание 1 устанавливается рабочий корпус камеры 2, выполненный обычно из прозрачного материала. Образец грунта 5 помещают в тонкую резиновую оболочку и устанавливают на нижний пористый штамп 7 с уплотнителем 12, прикрытый фильтровальной бумагой. Сверху образца также помещается бумажный фильтр и поверх него верхний пористый штамп 6. На рабочую камеру 2 устанавливается крышка с отверстием для корпуса штока 4 и вентиля для выпуска воздуха 3. Для создания герметичности верхняя крышка привинчивается болтами к камере 2. В основании камеры 1 имеются трубки 8 для оттока воды из образца и измерения давления в поровой воде, а также трубка 9 для заполнения камеры 2 водой и измерения в ней давления с помощью манометра 10. Для измерения вертикальных деформаций на шток устанавливается индикатор перемещений 11.

В такой конструктивной схеме имеются следующие особенности:

1. Образец грунта находится под действием всестороннего давления, равного боковому, а осевое давление не может быть меньше бокового.

2. При сжатии образца объем воды в камере меняется как в результате бокового расширения образца, так и вследствие вхождения в камеру части штока.

Конечной целью испытания является разрушение образца. Такое разрушение можно осуществлять разными путями, например, сохранять вертикальное давление и уменьшать боковое, либо, напротив, сохранять боковое давление постоянным и увеличивать вертикальное. Можно менять и оба напряжения одновременно по некоторому заданному режиму.

Испытания проводят в две стадии. На первой стадии образец загружают гидростатическим давлением, т.е. . Под гидростатическим давлением образец грунта выдерживают до затухания деформаций. Вертикальная деформация образца измеряется с помощью индикатора часового типа. Объемные деформации можно измерять, например, с помощью волюмометра, или оптической системы измерения деформаций. Далее вычисляются относительная продольная деформация e₁ и относительная объемная деформация.

На второй стадии боковое давление q сохраняется постоянным, а осевое давление ступенями увеличивают до разрушения образца. Каждая ступень нагружения выдерживается до условной стабилизации вертикальной деформации (например, для супесей и суглинков за критерий условной стабилизации принимается приращение относительной деформации 0,0001 за 6 часов). Для каждой ступени вычисляют относительные деформации и .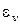

Для определения характеристик деформируемости строят график зависимости 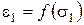. Вид такой зависимости приведен на рис. 3.24.

На графике 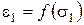, как правило, можно выделить линейный участок при , например участок . На этом участке имеем изменение вертикального напряжения 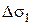, изменение вертикальной деформации 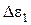, а также 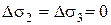, так как боковое давление остается постоянным. Применяя обобщенный закон Гука в форме приращений, получим:

 

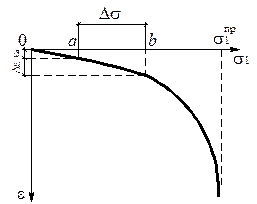
Рисунок 3.24. - Результаты стабилометрических испытаний

 

 

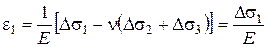, (3.52)

откуда

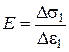(3.53)

На участке Оа имеем гидростатическое напряженное состояние. Тогда для точки можно записать:

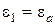(3.54)

Из обобщенного закона Гука имеем:

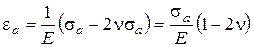, (3.55)

отсюда получаем значение коэффициента Пуассона

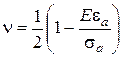(3.56)

При определении прочностных характеристик грунтов на стабилометре применяют различные схемы испытаний: недренированное, консолидированно - недренированное и дренированное. Методика и детали каждой схемы излагаются в ГОСТ 26518-85. Опуская детали, рассмотрим принципиальную сторону испытаний. Из рассмотрения диаграммы деформирования 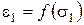, приведенной на рис. 3.24, видно, что при 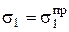и происходит разрушение образца, так как деформации образца 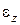неограниченно возрастают без увеличения напряжения . 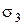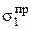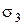Так как напряжения и являются главными, то на них как всегда можно построить круг Мора, и поскольку в точке напряжениия и являются разрушающими, круг Мора будет предельным. Проведем второе испытание образца, вырезанного из того же монолита грунта. Испытания проводятся по той же схеме, например, при постоянном боковом давлении 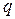. В этих опытах значения бокового давления 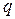принимают различными (например, q = 0,1 МПа, q = 0,2 МПа). Для каждого значения 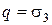будут получены соответствующие разрушающие напряжения 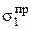. Нанесем результаты этих трех опытов на плоскость напряжений 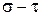и построим соответствующие круги Мора (рис. 3.25). В соответствии с теорией Мора-Кулона эти круги должны иметь общую огибающую, которой является предельная прямая Кулона. Ее угол наклона есть угол внутреннего трения j, а отрезок, который она отсекает на оси 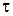, есть удельное сцепление с. Если построение выполнить в достаточно крупном масштабе, можно ограничиться графическим определением j и с.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: