Выражение (2.27) можно записать в виде 7 глава

и проинтегрируем

,

где ¦(q) - произвольная функция угла q (напомним, что вместо произвольной постоянной при интегрировании уравнения в частных производных добавляется произвольная функция от аргумента, по которому не производилось интегрирование).

Отсюда

,

и после потенциирования получаем

.

(4.44)

Произвольная функция ¦(q) должна удовлетворять третьему уравнению системы (4.32), т.е. уравнению совместности, и граничным условиям. Поскольку s_q º 0, то согласно (4.30) . Теперь возьмем производные, входящие в уравнение совместности

, , .

и подставим их в это уравнение. В результате придем к уравнению

.

Известно, что общий интеграл этого уравнения имеет вид:

,

(4.45)

где C, C ₁ - произвольные постоянные.

При определении C, C ₁ прежде всего необходимо учесть, что вертикальная координатная плоскость уОz является плоскостью симметрии напряженно-деформированного состояния основания. Это означает, что знак угла q не должен влиять на величину s _r. Следовательно, функция ¦(q) должна быть четной, т.е. должна удовлетворять условию ¦(q) = ¦(-q). Этому требованию удовлетворяет первое слагаемое в (4.45). Поэтому необходимо положить C ₁ = 0, и выражение (4.44) принимает более определенный вид:

.

(4.46)

Остается определить константу C. С этой целью радиусом r вырежем из основания (рис. 4.13) полуцилиндр в направлении оси Oy длиной, равной единице. Под действием нагрузки p и напряжения s _r он должен находиться в равновесии. В силу указанной симметрии необходимо удовлетворить только уравнению S Z = 0, остальные два уравнения S X = 0, S Y = 0 удовлетворяют автоматически.

 

Рисунок 4.13. - Схема к условию равновесия полуцилиндрического тела в задаче Фламана

 

Для составления уравнения S Z = 0 выделим на круглоцилиндрической поверхности полуцилиндра элементарную площадку шириной rd q и длиной 1. Ее площадь d q = 1∙ rd q (см. рис. 4.13). На эту площадку действует элементарная сила

,

направленная по радиусу. Ее проекция на ось Oz равна , а с учетом выражения (4.46) будет . В сумме элементарные силы должны уравновешивать нагрузку p. Таким образом, уравнение равновесия S Z = 0 полуцилиндра принимает вид:

.

Входящий сюда интеграл легко берется после подстановки равенства :

.

В результате находим значение произвольной постоянной

.

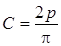Подставив найденное значение С в (4.46), окончательно получим

.

(4.47)

Согласно формуле (4.47), линии s _r = const представляют собой окружности, касающиеся поверхности основания в начале координат, как изображено на рис. 4.14. Действительно, для этого достаточно формулу (4.47) записать в виде

,

где - диаметр круга, касающегося поверхности в начале координат.

 

Рисунок 4.14. - Линии равных значений радиального напряжения в задаче Фламана

 

Задача определения напряженного состояния основания решена, поскольку определены главные напряжения s₁ = s _r и их направления. Однако для практического применения удобнее иметь дело с компонентами напряжения s _x, s _z, t _xz. Необходимые преобразования можно выполнить с помощью известных формул

;

.

Полагая здесь s₁ = s _r; s₃ = s_q = 0 и учитывая, что главное напряжение в решаемой задаче составляет с осью Oz угол a = q, будем иметь

; .

Имея в виду равенства

, ,

и формулу (4.47) получим

, , .

(4.48)

Наконец, заменим здесь полярные координаты прямоугольными, используя зависимости между ними:

; ; .

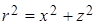В результате получим

, , .

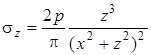(4.49)

Кроме этих напряжений, нормально к любой плоскости, параллельной плоскости хОz, действуют главные напряжения s _y = s₂. Их величину можно определить из закона Гука для условия плоской деформации e _y = 0. Согласно (4.8)

.

Подставив сюда выражения для s _x и s _z из (4.49), получим

.

Найденные формулы для напряжений (4.47) и (4.49) можно получить, если задаться функцией напряжений в виде:

в полярной системе координат

,

в декартовой системе координат

.

Для того чтобы наглядно охарактеризовать напряженное состояние в задаче Фламана, на рис. 4.15 приведены эпюры напряжений s _x, s _z, t _xz в двух горизонтальных сечениях, а также эпюра напряжения s _z вдоль оси Oz. Эпюры s _x, s _z симметричны относительно оси Oz, причем первая имеет на оси Oz максимальное значение, а вторая равна нулю. Отметим еще, что все напряжения на любой прямой, проходящие через начало координат, уменьшаются в обратном отношении к расстоянию r и при обращаются в нуль, а при неограниченно растут. Например, вдоль вертикальной оси Oz x = 0, тогда выражение (4.49) для s _z примет вид

Рисунок 4.15. - Эпюры напряжений в основании в задаче Фламана

 

.

Взяв соответствующие пределы при , имеем

, .

На примере вывода формулы осадки в задаче Фламана покажем, как определяются деформации и перемещения, если известны напряжения.

Согласно закону Гука (4.16) и уравнениям Коши (4.17)

Отсюда после подстановки выражения для напряжений (4.49) и интегрирования получим

,

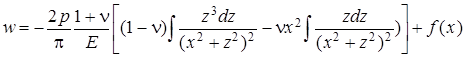где ¦(x) - произвольная функция x.

Входящие в это выражение интегралы можно найти в любой справочной таблице интегралов

,

.

После их подстановки будем иметь

.

Осадки точек поверхности основания получим, положив здесь , :

.

Предположим, что при имеем . Тогда

.

Подставив значение ¦(x) в предыдущее выражение, окончательно получим

,

(4.50)

где C - произвольная постоянная в силу произвольности величины s.

Таким образом, в задаче Фламана осадку можно определить только с точностью до произвольного слагаемого.

График осадки поверхности основания показан на рис. 4.16. Видно, что в начале координат осадка бесконечно велика. Сосредоточенная погонная нагрузка как бы прорезает основание. Такой результат является следствием того, что напряжения с приближением к точке приложения силы теоретически возрастают до бесконечности, поскольку площадь опирания силы равна нулю. По закону Гука из этого следует, что и деформации здесь бесконечно велики, а вместе с ними, согласно зависимости Коши, бесконечно велики и перемещения. Вместе с тем необходимо помнить, что деформации должны быть достаточно малы.

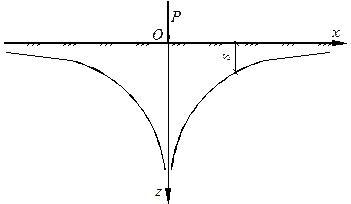
Рисунок 4.16. - Осадка поверхности основания в задаче Фламана

 

 

4.5.2. Задача о произвольной полосовой нагрузке

 

Выделим на поверхности основания полосу постоянной ширины b = 2 a (рис. 4.17) и бесконечной длины. К ней приложим давление, изменяющееся поперек полосы по некоторому закону p = p (x). Вдоль полосы давление не меняется. Ставится задача - определить напряженно-деформированное состояние основания от такой нагрузки.

Рисунок 4.17. - Схема к определению напряжений в основании от полосовой нагрузки, распределенной по произвольному закону

 

Возьмем в основании произвольную точку M с координатами x, z, а на полосе загружения на расстоянии x от начала координат выделим бесконечно узкую полоску шириной d x. Приложенное к полоске давление заменим бесконечно малой сосредоточенной силой dP = p (x) d x. Расстояние от точки приложения этой силы до точки M определяется координатой z и разностью x - x. Используя формулы Фламана (4.49), можно определить бесконечно малые величины напряжений в точке М от силы dP. Для этого достаточно в формулах (4.49) заменить нагрузку p на p (x) d x, а координату x на x - x:

, , .

(4.51)

Напряжения в точке M, очевидно, получим, проинтегрировав эти выражения по всей ширине полосы загружения:

, , .

(4.52)

На этом, собственно, можно и закончить определение напряженного состояния основания от полосовых нагрузок, поскольку дальше следует чисто математическая операция взятия записанных интегралов. Сложность этой операции зависит от сложности закона распределения давления p (x). В аналитическом виде решения получены, в частности, для равномерного давления =const (см. следующий пункт), для треугольного закона распределения давления поперек полосы. Суперпозиция этих двух решений дает выражение для трапецеидального закона давления. Получены решения и для некоторых других законов распределения давления. Но даже если закон p (x) настолько сложен, что интегралы в (4.52) не берутся, их всегда можно вычислить приближенно, заменив интегрирование суммированием.

 

4.5.3. Задача о равномерной полосовой нагрузке (задача Мичелла,

1902 г.)

 

Эта задача является наиболее важной в практическом отношении, поскольку считается, что длинный, так называемый ленточный фундамент, центрально загруженный сосредоточенной силой, создает равномерное полосовое давление на основание. В этом же случае наиболее просто выполняется интегрирование в формулах (4.52). Однако предпочтительнее получить решение в переменных r, q, используя в качестве исходных формулы задачи Фламана (4.48). Полученные при этом формулы имеют более компактный вид.

На полосе загружения выделим элементарную полоску шириной dx и из произвольной точки основания М (рис. 4.18) проведем в края этой полоски лучи. Из элементарного прямоугольника треугольника ABC имеем . Приложенное к полоске давление p ₀ заменим элементарной сосредоточенной силой . Используя формулы (4.48), определим бесконечно малые значения напряжений в точке М:

 

Рисунок 4.18. - Схема к определению напряжений в основании от равномерной полосовой нагрузки

 

 

, , .

Отсюда

, , .

В результате интегрирования имеем

; ; .

(4.53)

Эти формулы можно преобразовать к более компактному виду, если ввести углы b, d с помощью равенств

, , , .

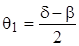(4.54)

Подставляя пределы интегрирования в (4.53) и заменяя углы q₁ и q₂ на b и d, имеем

;

 

;

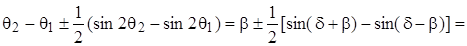
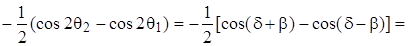
теперь формулы (4.53) могут быть переписаны так:

; .

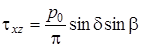(4.55)

В соответствии с этими формулами показано распределение компонент напряжений в двух вертикальных и горизонтальных сечениях в основании (рис. 4.19).

 

Рисунок 4.19. - Эпюры напряжений s _z в основании от равномерной полосовой нагрузки

интенсивностью p ₀

 

С помощью этих формул и формул преобразования напряжений

определим главные напряжения

.

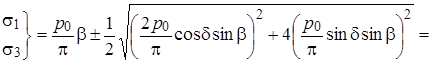
Окончательно имеем

.

(4.56)

Отметим, что угол b - это угол, при котором видна полоса загружения из точки М (см. рис. 4.18). Поэтому он получил название угол видимости.

Далее можно показать, что наибольшее главное напряжение s₁ направлено по биссектрисе угла видимости. Действительно, угол a между осью Oz и направлением s₁ определяется формулой

.

Подставляя сюда выражение (4.55), получим

.

Отсюда с учетом второго из равенств (4.54)

.

Полученное равенство доказывает, что линия действия главного напряжения s₁ проходит по биссектрисе угла видимости.

С помощью формул (4.56) можно проанализировать распределение главных компонент напряжений в основании. В качестве примера на рис. 4.20 показано распределение главных компонент напряжений и отношения .

Рисунок 4.20. - Линия равных значений главных напряжений в основании от равномерной полосовой нагрузки

 

Кроме приведенных напряжений нормально к любой плоскости, параллельной плоскости xOz, согласно формуле (4.8) действуют напряжения

.

На сегодняшний день, учитывая доступность персональных ЭВМ, удобно использовать формулы для компонент напряжений в декартовой системе координат

,

.

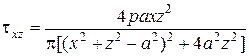Осадку поверхности основания в рассматриваемой задаче проще всего определить с помощью формулы осадки в задаче Фламана (4.50). Для этого с помощью формулы (4.50) запишем бесконечно малую осадку в некоторой точке поверхности с координатой x от бесконечно малой силы p ₀ d x, расположенной в пределах полосы загружения на расстоянии x от начала координат:

.

При интегрировании этого выражения следует отдельно рассмотреть случай и случай .

Объединяя эти два результата для точек поверхности основания, расположенных справа от начала координат, с точностью до произвольного слагаемого, можем записать

, .

(4.57)

Верхние знаки здесь относятся к точкам интервала , а нижние - точкам интервала . График правой половины симметричной относительно начала координат эпюры осадки показан на рис. 4.21.

 

 

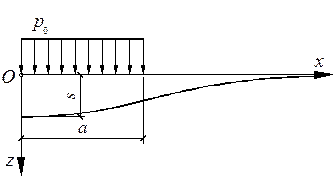
Рисунок 4.21. - Эпюры осадки поверхности основания от полосовой равномерной нагрузки

 

 

4.5.4. Задача о треугольной полосовой нагрузке

 

Эта задача имеет значение для строителей железных и автомобильных дорог, поскольку может использоваться при определении напряжений в основаниях насыпей. Если разбить трапецеидальную нагрузку от насыпи на основание на три - равномерно распределенную интенсивностью p и две симметричные треугольные, то, применяя принцип суперпозиции, в каждой точке основания можно отдельно определять напряжения от каждой из трех составляющих общей нагрузки, а затем их складывать.

Напряжения от равномерной нагрузки интенсивностью p нами рассмотрены выше (п. 4.5.3). Напряжения в точке M (x, z), возникающие в основании от действия одиночной треугольной полосовой нагрузки (рис. 4.22), могут быть найдены по формулам (Польшин, 1933):

,

, (4.58)

.

 

 

Рисунок 4.22. - Схема к определению напряжений в основании от треугольной

полосовой нагрузки

 

Вертикальное перемещение точек поверхности в случае действия одиночной треугольной нагрузки составит:

. (4.59)

 

4.5.5. Задача о погонных нагрузках, приложенных на некоторой глубине внутри основания (задача Мелана, 1932)

 

В заключение параграфа о плоских задачах определения дополнительных напряжений в линейно-деформируемом основании, ограниченном горизонтальной плоскостью, приведем два наиболее общих решения. Оба решения были даны Е. Меланом в 1932 г., а затем уточнены М.И. Горбуновым-Посадовым в 1954 г.

Пусть на некоторой глубине d действует вертикальная погонная нагрузка интенсивностью p (рис. 4.23). В этом случае функция напряжений имеет вид:

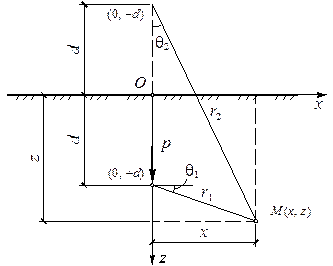
Рисунок 4.23. - Схема к определению напряжений в основании в задаче Мелана

для вертикальной погонной нагрузки

 

 

(4.60)

Тогда компоненты напряжений определятся следующими зависимостями:

(4.61)

 

(4.62)

 

(4.63)

Нетрудно убедиться, что пр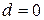и и представленные зависимости совпадают с решением Фламана.

Запишем далее выражения для перемещений

(4.64)

где , .

Предположим теперь, что некоторой глубине d действует горизонтальная погонная нагрузка интенсивностью q, направленная как показано на рис. 4.24. В этом случае функция напряжений имеет вид:

Рисунок 4.24. - Схема к определению напряжений в основании в задаче Мелана

для горизонтальной погонной нагрузки

 

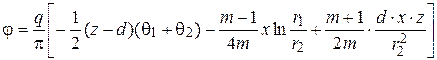. (4.65)

Напряжения и перемещения точек среды равны

(4.66)

 

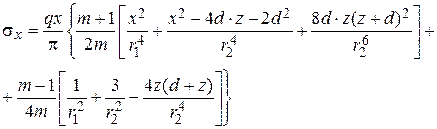(4.67)

 

(4.68)

 

(4.69)

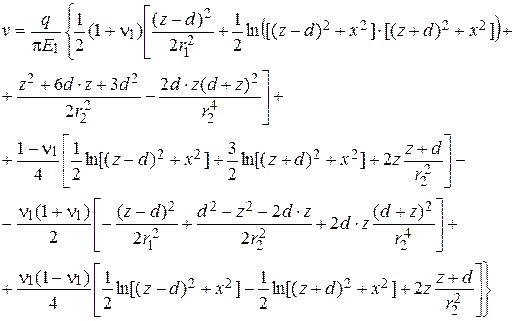
Используя приведенные зависимости и применяя принцип суперпозиции, можно получить выражения для напряжений, возникающих от действия как угодно сориентированной нагрузки, действующей на любой глубине или на поверхности, а затем, интегрируя, перейти от погонных нагрузок к полосовым. Таким образом, несмотря на громоздкость выражений (4.60)…(4.69), они могут быть полезны в практических расчетах для решения с помощью ЭВМ самых разнообразных задач о нагружении горизонтального изотропного однородного линейно-деформируемого основания.

 

4.6 Пространственная задача определения напряжений от внешних нагрузок

 

4.6.1. Задача о сосредоточенной силе (задача Буссинеска, 1885 г.)

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: