Выражение (2.27) можно записать в виде 2 глава

График сдвига песчаного грунта показан на рис. 3.6. Следует иметь в виду, что и чистые пески при определенной влажности обладают некоторым сцеплением. Крупнообломочные грунты, хотя и не обладают сцеплением в физическом смысле, т.е. связностью, при сдвиге имеют график, аналогичный глинистым грунтам. Роль сцепления в этом случае играет так называемое «зацепление» между крупными обломками.

 

Рисунок 3.6. - График сдвига несвязного грунта

Оценка прочности грунтов для условий пространственного напряженного состояния, т.е. оценка прочности грунта в точке, выполняется с использованием закона Кулона о прочности грунта на сдвиг. В основу оценки прочности грунта в точке положено следующее условие: предельное сопротивление грунта действующим напряжениям в точке считается достигнутым, если хотя бы на одной площадке, проходящей через эту точку, касательные напряжения достигли предельного сопротивления грунта сдвигу в соответствии с законом Кулона.

Как известно из курса «Сопротивления материалов», пространственное напряженное состояние грунта в точке можно представить графически в виде трех кругов Мора (рис. 3.7). Круги Мора строятся в координатах (s, t), центр круга располагается на оси s и диаметры кругов составляют 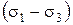, 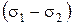и . Каждой точке круга Мора отвечает некоторая площадка, по которой действуют нормальные и касательные напряжения, являющиеся координатами этой точки. Таким образом, круги Мора дают наглядное представление о напряженном состоянии на различных площадках.

 

 

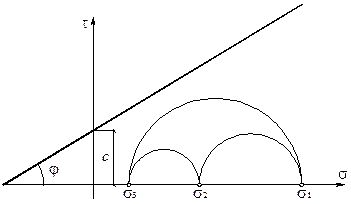
Рисунок 3.7. - Допредельное напряженное состояние в точке

 

Для оценки прочности грунта в точке следует диаграмму Мора совместить с графиком сдвига. Если круги Мора расположены ниже прямой Кулона, то напряженное состояние квалифицируется как допредельное (рис. 3.7). Если круг Мора наибольшего диаметра 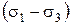касается прямой Кулона (рис. 3.8), то следует считать, что имеет место предельное напряженное состояние грунта в точке. Аналитически факт касания прямой Кулона круга Мора с диаметром 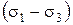записывается в виде:

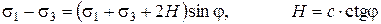. (3.12)

Эту формулу можно получить из рассмотрения прямоугольного треугольника ABC:

, , ,

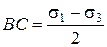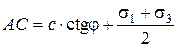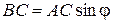или:

,

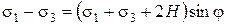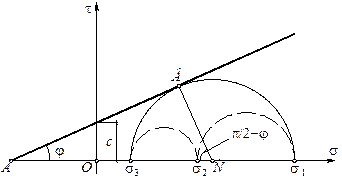
Рисунок 3.8. - Предельное напряженное состояние в точке

 

Условие допредельного напряженного состояния можно записать в виде строгого неравенства:

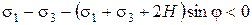. (3.13)

Таким образом, условие прочности грунта в точке для общего случая при наличии в грунте связности (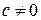) и внутреннего трения (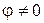) имеет вид:

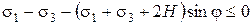. (3.14)

Выражение (3.14) называется условием прочности грунта Кулона-Мора. Для глинистых грунтов при отсутствии внутреннего трения (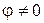) условие (3.14) приобретает вид:

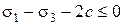. (3.15)

Отметим, что выражения (3.10) и (3.15) широко используются для сред, не обладающих внутренним трением, например, металлов, и представляют собой условие прочности Треска.

Для песчаных грунтов без сцепления () будем иметь:

. (3.16)

Условие Мора-Кулона определяет в пространстве главных напряжений 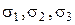соответствующую ему поверхность текучести. Определим эту поверхность. Уравнение (3.12) может рассматриваться как уравнение плоскости:

. (3.17)

Учитывая соотношение между главными напряжениями 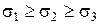, построим в пространстве главных напряжений еще две плоскости:

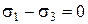, (3.18)

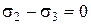. (3.19)

Часть плоскости (3.17), заключенная между плоскостями (3.18) и (3.19), является гранью шестиугольной пирамиды, имеющей своей осью прямую гидростатического напряжения (рис. 3.9). Поверхность этой пирамиды будет являться поверхностью текучести грунта Кулона-Мора. Функция текучести ¦ в соответствии с (3.12) записывается в виде:

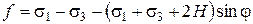. (3.20)

Выражение условия прочности Кулона-Мора в компонентах напряжений приведем только для случая, когда 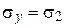. Тогда главные напряжения s₁ и s₃ определяются известными формулами:

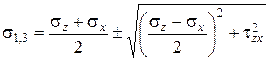. (3.21)

 

 

 

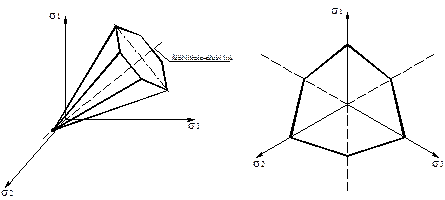
Рисунок 3.9. -Поверхность текучести Кулона-Мора в пространстве главных напряжений

 

 

Функция текучести и условие прочности Кулона-Мора примут вид:

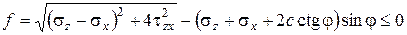. (3.22)

Разработан ряд условий прочности грунта в точке, отличающихся от рассмотренного условия. Однако в практике расчетов грунтовых массивов наибольшее применение находит рассмотренное условие прочности Кулона-Мора.

Применение к грунтам модели жесткопластического тела позволило решить большой круг практических задач по оценке устойчивости грунтовых оснований, откосов и склонов. Эти решения будут рассмотрены в главе 5.

 

3.2.3. Понятие об упругопластических и упруговязкопластических моделях грунта

 

В модели упруго-пластического тела рассматривается особый вид пластических (остаточных) деформаций. Это деформации пластического течения. Конечная величина таких деформаций может быть обусловлена только внешним препятствием их развитию, а не внутренними свойствами материала.

Основные положения модели упруго-пластического тела рассмотрим только для условий двумерной (плоской) задачи в координатной системе (z, x). Уравнение состояния грунта (зависимости между напряжениями и деформациями) будет записываться в дифференциальной форме, т.е. в виде связи между приращениями напряжений и приращениями деформаций.

В простейшей упруго-пластической модели рассматривается деформирование грунта в двух стадиях работы - в допредельном напряженном состоянии и в предельном напряженном состоянии. Соответственно, для описания подобного поведения материала прежде всего принимается функция текучести ¦. Для грунтов используется функция текучести Кулона-Мора (3.22):

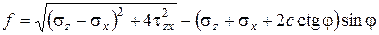. (3.23)

При 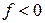имеет место допредельное напряженное состояние. Здесь грунт работает в соответствии с уравнением состояния линейно-деформируемого тела. Заметим, что термин «упругость» в названии модели носит условный характер, отражая лишь линейную связь между приращениями напряжений и деформаций.

Для условий плоской деформации (см. главу 4) уравнения состояния (3.3) имеют вид

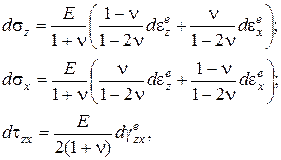(3.24)

где 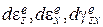- приращения условно «упругих» относительных деформаций.

При предполагается, что в грунте одновременно развиваются и «упругие», и пластические деформации. Полные деформации представляются в виде суммы «упругой» и пластической составляющей:

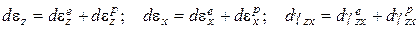, (3.25)

где - приращения относительных деформаций пластического течения.

Деформации пластического течения определяются зависимостями:

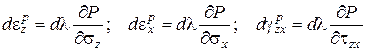. (3.26)

В приведенных зависимостях представляет собой некоторую функцию от напряжений и , называемую пластическим потенциалом, а - неопределенный множитель. Выражения (3.26) представляют собой закон пластического течения. Неопределенность означает, что этот параметр может принимать любые значения, т.е. свойства тела не ограничивают возможности развития деформаций пластического течения. В рассматриваемом варианте упругопластической модели в качестве пластического потенциала используется функция текучести 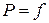. Тогда уравнения (3.26) примут вид:

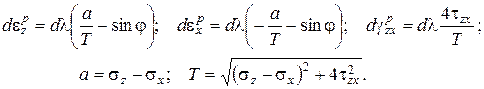(3.27)

Деформирование в упругопластической стадии сопровождается изменением напряженного состояния. При этом напряжения должны оставаться на поверхности текучести. Это обстоятельство учитывается уравнением:

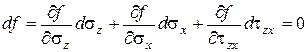. (3.28)

Совместное решение системы уравнений (3.24), (3.25), (3.27) и (3.28) приводит к следующему уравнению состояния грунта:

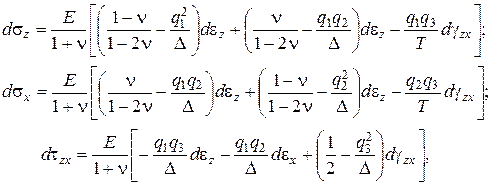(3.29)

где ;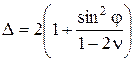

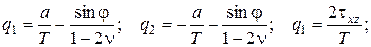
- см. формулу (3.27).

Применение модели упругопластического тела позволяет рассчитывать зарождение и развитие областей разрушения грунта в грунтовых массивах.

Сделаем несколько замечаний по поводу приведенных рассуждений. Прежде всего, следует помнить, что выражение (3.25), по сути, является гипотезой. Далее, выражение для пластического потенциала иногда записывают в ином виде, например,

.

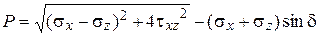Если 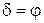, то после подстановки в (3.26) имеем ассоциированный закон пластического течения (3.27), если 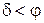- неассоциированный закон. Переписав закон пластического течения (3.26) и (3.27) в главных напряжениях и деформациях, можно показать, что

,

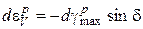где 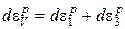- приращение относительной объемной деформации, 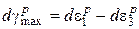- приращение максимальной деформации сдвига.

Последнее равенство означает, что сдвиг сопровождается отрицательной объемной деформацией. Согласно используемому в механике грунтов правилу знаков получаем при сдвиге увеличение объема - разрыхление. Это явление называется дилатансией. Грунты, преимущественно песчаные, в разной степени действительно обладают этим свойством, однако, принимая ассоциированный закон и 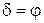, получают разрыхление настолько большое, что это явно противоречит опытным данным, и тогда встает вопрос о назначении величины угла d.

В модели упруго-вязкого тела рассматриваются преимущественно конечные пластические деформации. Термин «упругость» и здесь применяется условно. Если конечные пластические деформации возникают не мгновенно, а развиваются во времени, то считается, что грунт проявляет свойство ползучести. Ползучесть - это развитие деформаций во времени при постоянном напряжении. Обратное свойство - релаксация - это уменьшение напряжений при неизменной деформации. Эти процессы описываются с помощью модели упруго-вязкого тела [5].

Рассмотрим основные положение упруговязкой модели на примере одноосного напряженного состояния. Пусть к образцу связного грунта мгновенно приложено сжимающее напряжение s, не изменяющееся во времени. Характерный график деформирования образца показан на рис. 3.10. Часть деформации реализуется быстро, теоретически мгновенно - e_мгн, дальнейший процесс сжатия проистекает во времени, теоретически до бесконечности - e_¥. Процесс развития деформаций ползучести e(t) может быть представлен в виде [24]:

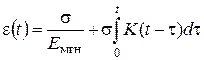, (3.30)

где 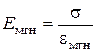- мгновенный модуль деформации, 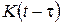- ядро ползучести - экспериментальная функция от аргумента 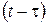, определяющая скорость деформации в момент времени 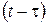при единичном напряжении.

 

 

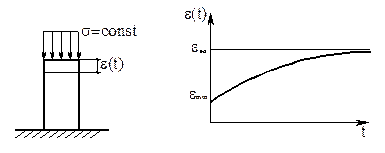
Рисунок 3.10. - Ползучесть образца глинистого грунта при постоянном напряжении.

 

Выражение (3.30) для одномерной задачи и постоянной нагрузки является частным случаем уравнения состояния модели линейно-наследственной ползучести грунта при постоянном напряжении.

На рис. 3.11 показан образец связного грунта, мгновенно сжатый с относительной деформацией e, не изменяющейся во времени. На графике показано уменьшение во времени напряжения (релаксация напряжения) в этом образце. Процесс релаксации напряжений можно выразить формулой, аналогичной по форме уравнению (3.30):

, (3.31)

где 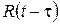- ядро релаксации - экспериментальная функция от аргумента 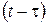, определяющая скорость уменьшения напряжения в момент времени 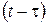при единичной деформации.

 

 

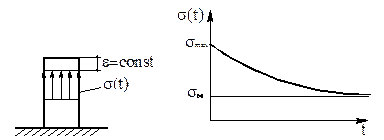
Рисунок 3.11. - Релаксация напряжения в образце глинистого грунта при постоянной

деформации.

 

 

Если, помимо мгновенного модуля деформации E _мгн, ввести понятие модуля

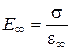(3.32)

то, учитывая зависимость между напряжением и скоростью деформации 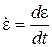в процессе вязкоупругого деформирования в виде 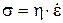, где h - коэффициент вязкости, ядра ползучести и релаксации определятся как

, (3.33)

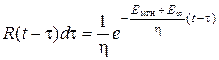. (3.34)

Модель упруго-вязкого деформирования позволяет рассчитывать развитие затухающих деформаций грунта во времени.

 

3.2.4. Понятие о консолидирующемся грунте. Двухфазная модель грунта. Принцип эффективных напряжений Терцаги

 

В инженерной практике довольно часто встречаются основания, сложенные полностью водонасыщенными глинистыми грунтами. Эти грунты представляют собой двухфазную среду, состоящую из скелета грунта и поровой воды. Наличие пузырьков воздуха в поровой воде придает системе определенную упругость, но в принципе не меняет сути ее работы. Двухфазная модель грунта - это пористая среда, полностью заполненная водой, называемая грунтовой массой.

Исходя из положения о практической несжимаемости твердых минеральных частиц и поровой воды, можно сделать вывод о том, что деформирование полностью водонасыщенного глинистого грунта, по крайней мере его сжимаемость, может реализоваться только при условии отжатия воды из пор грунта. Отжатие воды из пор грунта относится к процессу фильтрации, как правило, в ламинарном режиме, и описывается законом Дарси. Фильтрация воды вызывается системой дополнительных напоров в поровой воде, определяющих траекторию движения воды в места разгрузки, к поверхности грунтового массива.

С другой стороны, объем и форму грунта полностью определяет его скелет. Следовательно, деформации грунта суть деформации его скелета. Поскольку эти деформации обуславливаются напряжениями, то система возникающих напряжений в скелете является причиной его деформаций.

Таким образом, внешняя нагрузка на полностью водонасыщенные грунты вызывает в них дополнительные напряжения, распределяющиеся между скелетом грунта и поровой водой. Напряжения в скелете грунта называются эффективными напряжениями, а давление в воде - поровым давлением. Тогда полные напряжения в грунте определятся как

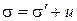, (3.35)

где s¢ - эффективные напряжения, u - поровое давление.

Разумеется, поровая вода воспринимает только гидростатическое давление, а сдвиговые напряжения полностью передаются на скелет грунта.

Скорость фильтрации воды обуславливает скорость деформирования скелета грунта или «видимого» грунта в целом. С течением времени, по мере отжатия воды из пор грунта и его уплотнения, скелет грунта примет на себя все дополнительные напряжения и наступит процесс стабилизации деформаций.

Рассмотренный процесс уплотнения полностью водонасыщенного глинистого грунта называется процессом консолидации, или просто консолидацией, а указанные грунты - консолидирующимися грунтами. В песчаных грунтах также имеет место данный процесс, но вследствие высокой водопроницаемости песков протекает он быстро и практического интереса, как правило, не представляет. Поэтому, к консолидирующимся грунтам относят, прежде всего, полностью водонасыщенные супеси и суглинки.

Таким образом, деформирование консолидирующихся грунтов развивается во времени пропорционально их водопроницаемости. Движение воды в пористой грунтовой среде описывается законом ламинарной фильтрации Дарси. Деформируемость скелета грунта может быть описана любой из выше рассмотренных моделей линейно-деформируемого, жесткопластического, упругопластического или упруговязкого тела. Подробное математическое описание процесса консолидации будет рассмотрено в шестой главе.

Здесь же приведем формулировку принципа эффективных напряжений К. Терцаги: любые видимые деформации полностью водонасыщенного глинистого грунта (консолидирующегося грунта) определяются деформациями его скелета, а следовательно, действующими в нем эффективными напряжениями. Все методики определения деформационных и прочностных характеристик, которые будут рассмотрены ниже и которые регламентированы действующими стандартами, характеризуют деформации и прочность именно скелета. Это значит, что обобщенный закон Гука и закон Кулона подразумевают использование эффективных напряжений. В частности, закон Кулона в эффективных напряжениях имеет вид [31]:

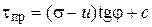. (3.36)

Эта выражение в механике грунтов имеет самостоятельное значение и называется формулой Терцаги.

В заключение отметим, что для таких грунтов часто используется теория плотности-влажности проф. Н.Н. Маслова [22]. В основу данной теории положено представление о том, что на каждом этапе консолидации соответствующим значениям плотности и влажности грунта будут отвечать свои параметры прочности, т.е.

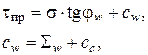(3.37)

где j _w, c_w - параметры прочности, соответствующие данной плотности и влажности грунта, S _w - связность грунта, обусловленная водноколлоидными связями, восстанавливаемая часть сцепления, c_c - структурное сцепление, не восстанавливаемая часть.

Наиболее полный обзор моделей грунта можно найти в [34].

3.3. Компрессионные испытания грунтов. Определение деформационных характеристик

 

Изучение деформируемости конструкционных материалов, как правило, производится при одноосных испытаниях на растяжение или сжатие цилиндрических или призматических образцов. Такие опыты легче всего выполнить, а деформационные характеристики на их основе легко определить из закона Гука.

Для грунтов, образцы которых способны удерживать заданную форму, метод одноосных испытаний также применим, например, для тугопластичных глин. Такие опыты неоднократно проводились. Результаты этих опытов на растяжение-сжатие удобно представить на диаграмме (рис. 3.12). Из диаграммы видно, что:

- при сравнительно небольших напряжениях связь между деформациями и напряжениями линейная;

- на растяжение грунт работает значительно хуже, чем на сжатие;

- грунт разрушается путем пластического течения, т.е. имеются соответствующие площадки и пределы текучести.

Однако одноосные испытания применимы далеко не ко всем грунтам, так как многие грунты не способны сохранять заданную форму даже под действием собственного веса (например, сухие пески или глинистые грунты текучей консистенции). Таким образом, одноосные испытания для грунтов не являются универсальными. Впервые универсальный метод исследования деформационных свойств грунтов был предложен К. Терцаги. Этот способ получил название компрессионного метода.

 

 

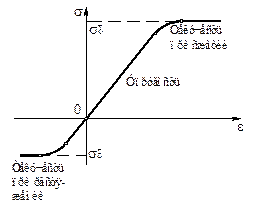
Рисунок 3.12. - Результаты одноосных испытаний тугопластичных глин

 

Под компрессией понимается исследование сжимаемости грунтов без возможности бокового расширения. Испытания проводятся в специальных приборах - одометрах, или компрессионных приборах [40]. Грунт при испытании помещается в жесткую недеформируемую цилиндрическую обойму и в ней обжимается вертикальной нагрузкой через рычажную систему. Принципиальная схема такого прибора и его конструкция показана на рис. 3.13 и особых пояснений не требует. Отметим лишь, что наличие отверстий в верхнем и нижнем штампах является обязательным, чтобы обеспечить отток воды из образца при его сжатии. Для снижения сил трения грунта о стенки обоймы принимается определенное соотношение высоты и диаметра образца. Обычно высота образца принимается равной 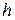= 25 мм, а его площадь A = 60 см² [12]. Наиболее распространенным по конструктивному оформлению является компрессионный прибор системы «Гидропроекта», вообще же таких конструкций много.

Испытания образца грунта производят путем ступенчатого приложения вертикальной нагрузки s. Величина ступеней обычно принимается по 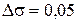МПа. Каждую ступень нагрузки выдерживают до затухания осадки (на практике обычно ограничиваются условной стабилизацией деформаций). Для каждой ступени нагружения с помощью индикатора часового типа измеряют абсолютную осадку s.

По результатам испытаний можно для каждой ступени вычислить относительную деформацию 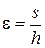и построить график зависимости . Такой график, приведенный на рис. 3.14, называется компрессионной кривой. Из графика видно, что при компрессионном испытании связь между относительными деформациями и напряжениями нелинейная. В небольших интервалах напряжений нелинейную зависимость без большой погрешности можно заменить линейными (рис. 3.14). Тангенс угла наклона спрямленного участка к оси s называют относительным коэффициентом сжимаемости и обозначают:

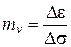. (3.38)

 

 

 

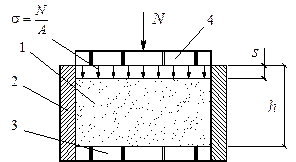
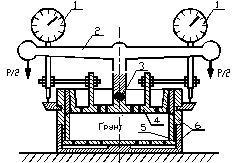
Рисунок 3.13. - Принципиальная схема (а) и конструкция компрессионного прибора (б)

Обозначения на схеме (а): 1 - грунт, 2 - жесткий корпус, 3 - пористое дно, 4 - пористый поршень. Обозначения на схеме (б): 1 - индикаторы перемещений, 2 - коромысло рычажного устройства, 3 - шарик, 4 - поршень, 5 - компрессинное кольцо, 6 - корпус

 

 

 

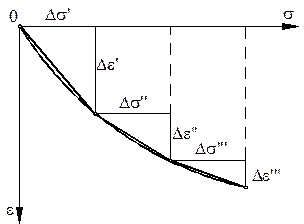
Рисунок 3.14. - Компрессионная кривая

 

 

Принимая вертикальную ось 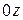, , заметим, что боковые напряжения в силу симметрии равны 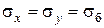. Тогда, из обобщенного закона Гука при отсутствии боковых деформаций 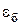=0 получим связь между вертикальным и боковым давлением:

,

отсюда

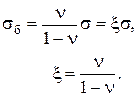(3.39)

Параметр x называется коэффициентом бокового давления в грунте при компрессии. Выражение для 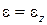будет иметь вид:

,

или

. (3.40)

Коэффициент b в формуле (3.40) учитывает компрессионные условия сжатия грунта. Поскольку грунт рассматривается как линейно деформируемая среда в небольшом интервале изменения напряжений, то вместо (3.40) следует записать:

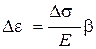. (3.41)

Из последнего выражения определяется модуль деформации грунта E:

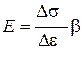. (3.42)

При производственных испытаниях модуль деформации чаще всего определяют на участке изменения s от 0,1 до 0,2 МПа или для того диапазона напряжений, в котором ожидается работа основания сооружения.

С использованием понятия относительного коэффициента сжимаемости m_v (3.38) выражение для модуля деформации можно записать также в виде

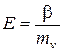. (3.43)

Очевидно, что, пользуясь только компрессионными испытаниями, модуль деформации определить невозможно, поскольку неизвестен коэффициент b, зависящий от коэффициента Пуассона n, который определить из обычных компрессионных испытаний нельзя. Однако экспериментально установлено, что коэффициент Пуассона незначительно меняется для данного вида грунта, поэтому для практических целей при определении компрессионного модуля деформации Е коэффициент Пуассона принимается по справочным данным в зависимости от вида грунта. В табл. 3.1 даны значения этого коэффициента.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: