Выражение (2.27) можно записать в виде 8 глава

 

Рассмотрим действие сосредоточенной вертикальной силы на поверхность полупространства. Эта задача считается основной в теории напряженного состояния оснований. Решение ее было получено Ж. Буссинеском в 1885 г.

На рис. 4.25 показана расчетная схема задачи в декартовой системе координат Oxyz: плоскость Oxy совпадает с горизонтальной поверхностью пространства, ось Oz вертикальна. Сосредоточенная вертикальная сила приложена в начале координат. Определим величину вертикальных сжимающих напряжений от этой силы.

Для произвольной точки М в основании обозначим радиусом r расстояние от начала координат, угол между радиусом r и осью Oz обозначим параметром q, угол между осью Ox и проекцией радиуса на плоскость Оху - параметром y. В окрестности точки М выделим элементарный объем, ограниченный двумя элементами шаровых поверхностей dA ₁, dA ₂ с радиусами r и и плоскими гранями, положение которых определяется углами d q и d y (см. рис. 4.25). На площадке dA ₁ действует радиальное напряжение s _r, на площадке dA ₂ - напряжение . Элементарные площади dA ₁ и dA ₂, пренебрегая малыми высших порядков, равны:

 

 

Рисунок 4.25. - К задаче Буссинеска

 

 

, .

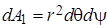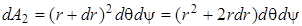Из уравнения равновесия выделенного элементарного объема имеем:

, ,

,

,

Пренебрегая величиной большего порядка малости , получим

.

Интегрируя это уравнение, приходим к выражению

, .

Функция ¦(q) должна удовлетворять следующим условиям: ¦(q) = -¦(q) в силу симметрии, согласно граничным условиям. Примем функцию (B = const), отвечающую указанным равенствам. Для нахождения константы B рассмотрим в основании полусферическую поверхность радиусом r (рис. 4.25). По этой полусфере будут действовать радиальные напряжения:

.

Составим уравнение равновесия всех сил на ось Oz для выделенной части основания:

.

(4.70)

Из этого уравнения найдем константу B:

.

Соответственно радиальные напряжения определятся формулой

.

Поскольку на сферической поверхности отсутствуют касательные напряжения, вертикальные напряжения можно найти по формуле

.

Переходя к декартовой системе координат, запишем выражение для s _z, в виде

,

где .

Приведем выражения для всех компонент напряжений в декартовой системе координат:

; ; ; ; ; .

(4.71)

Для перемещений параллельно осям координат даются формулы:

; ; .

(4.72)

Выражения для компонент деформаций нетрудно получить, подставляя (4.71) в обобщенный закон Гука (4.19).

Полученные зависимости также можно получить, если принять функцию напряжений в виде (в цилиндрических координатах Orz q):

, , , .

Наглядное представление об изменении напряжений в основании можно получить из рис. 4.15, где показаны эпюры вертикальных, горизонтальных нормальных и касательных напряжений в плоской задаче Фламана. Отличие в случае пространственной задачи Буссинеска заключается в том, что с глубиной уменьшение или рассеивание напряжений происходит быстрее, чем в плоской задаче.

 

4.6.2. Задача о произвольном нормальном давлении

 

Для определения напряжений и перемещений в основании при действии на его поверхности произвольной нормальной нагрузки используется решение Буссинеска о сосредоточенной силе и принцип суперпозиции.

На рис. 4.26 в декартовой системе координат изображена произвольная площадка A, на которую действует произвольное нормальное давление p (x, h), x, h - координаты нагрузки вдоль осей Ox и Oy. Выделив элементарную площадку , приложим к ней элементарную сосредоточенную силу . Тогда в произвольной точке M с координатами x, y, z по формулам (4.71) можно найти бесконечно малые величины напряжений и перемещений от силы dP. Проинтегрировав полученные выражения по площади загружения A, найдем искомые напряжения и перемещения в точке M от заданной нагрузки. Например, для вертикального напряжения s _z справедливо выражение

;

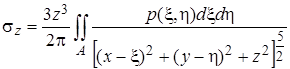(4.73)

где A указывает на действие интегрирования в пределах всей загруженной площадки.

Аналогичные выражения можно записать и для остальных компонент напряжений и перемещений.

 

Рисунок 4.26. - Расчетная схема загруженной площадки произвольной формы

 

 

4.6.3. Задача о равномерном давлении (задача Лява-Короткина 1929, 1938). Формула Шлейхера

 

Решение задачи о равномерно нагруженной прямоугольной площадке наиболее часто используется в практических расчетах. А. Лявом в 1929 г. были получены выражения для сжимающих напряжений s _z, а впоследствии В.Г. Короткин (1938 г.) получил формулы для всех компонент напряжений. Поэтому рассматриваемое решение называют задачей Лява-Короткина.

Приведем некоторые результаты упомянутых решений. На рис. 4.27 показана прямоугольная площадка размером , загруженная нормальным давлением интенсивностью p. Обозначим - меньший размер загруженной площади. Центр декартовой системы координат помещен в угол площадки, а оси Ox и Oy сориентированы по ее сторонам. Рассмотрим точку M на оси Oz, расположенную на глубине z под углом загруженного прямоугольника. Пользуясь приемом, изложенным в предыдущем параграфе, в соответствии с формулой (4.73) и обозначениями на рис. 4.27 запишем выражение для вертикального напряжения в точке M:

.

(4.74)

Введем обозначения , и запишем результат интегрирования выражения (4.74) в виде

= = .

(4.75)

 

 

 

Рисунок 4.27. - Расчетная схема задачи Лява-Короткина

 

Выражение, обозначенное , называется коэффициентом рассеивания напряжений и зависит, как видно из формулы (4.75), от соотношения сторон загруженного прямоугольника n и относительной глубины расположения рассматриваемой точки m. Индекс «угл» показывает, что данное выражение справедливо для точек, расположенных под углом загруженной площадки.

Приведем еще две формы записи выражений для вертикальных напряжений в точках, находящихся либо под краем (углом) загруженной площади, либо под ее центром

;
,	(4.76)

где - полуширина загруженной площади, l - половина ее длины.

Из выражений (4.76) следует, что напряжения в точке, находящейся под центром площади на глубине z = h в 4 раза больше, чем в точке, находящейся под краем площади на глубине z = 2 h, т.е.

,

(4.77)

Пользуясь выражением для вертикального перемещения задачи Буссинеска (4.72), запишем формулу для величины w в точках под углом загруженного прямоугольника:

= = ,

(4.78)

Коэффициенты A и B, как и коэффициенты рассеивания напряжений, зависят только от соотношений n и m. В рассматриваемом случае они равны

;

.

При различной в плане площади нагружения в выражении (4.78) коэффициенты A и B, очевидно, будут определяться иначе или вообще могут представлять собой неберущиеся интегралы.

Применяя принцип суперпозиции выражение (4.78) можно переписать для точки, находящейся под центром загруженной площади

,

(4.79)

где w - коэффициент формы, зависящий от формы площади нагружения.

Выражение (4.79) называется формулой Шлейхера и имеет самостоятельное практическое значение. Согласно действующим нормам его используют для расчета модуля деформации грунта в штамповых испытаниях (см. п. 3.8.2). Кроме этого, его можно применять для определения осадок однородного основания.

 

4.6.4. Метод угловых точек

 

Формулы (4.75)…(4.76) для расчета напряжения s _z под углом загруженной равномерным давлением прямоугольной площадки с помощью принципа суперпозиции позволяет определить вертикальное напряжение s _z в любой точке основания. Для этого составляется ряд условных прямоугольных загруженных площадок, для каждой из которых рассматриваемая точка находится под углом. В сумме загруженные площадки должны давать исходную нагрузку. Такой прием определения s _z называют методом угловых точек. Используя метод угловых точек, можно найти напряжения в основании от загруженных равномерным давлением площадок различных очертаний, которые можно составить суммированием ряда прямоугольников.

Рассмотрим несколько примеров. На рис. 4.28, а, б, в показан ряд загруженных площадок и положение в плане точки M. Напряжение s _z для приведенных случаев можно рассчитать по формулам:

 

Рисунок 4.28. - К методу угловых точек

 

 

Цифры у коэффициентов a показывают прямоугольники, для которых определяется a (индекс «угл» опущен).

Нетрудно заметить, что для точек, лежащих под центром загруженной площадки, будет справедливо выражение (4.77), уже записанное нами ранее,

.

(4.80)

Для облегчения практических расчетов составлены специальные таблицы значений коэффициентов рассеивания напряжений a_угл и a_центр. Иначе эти коэффициенты можно найти из формул (4.76).

Метод угловых точек можно распространить и для определения вертикальных перемещений любой точки основания. Тогда нужно выполнять аналогичные операции с коэффициентами A и B из формулы (4.78).

 

4.6.5. Задача о сосредоточенных силах, приложенных на некоторой глубине внутри основания (задача Миндлина, 1936 г.)

 

Здесь приведем задачу о вертикальной и горизонтальной сосредоточенных силах, приложенных внутри основания на некоторой глубине. Аналогичные решение уже были нами рассмотрены в плоской постановке в п. 4.5.5. Расчетная схема задачи о вертикальной силе дана на рис. 4.29., а о горизонтальной силе в декартовых координатной системе - на рис. 4.30. Эти задачи были решены Миндлиным в 1936 г.

 

 

Рисунок 4.29. - Схема к определению напряжений в основании в задаче Миндлина

для вертикальной сосредоточенной силы

 

 

Приведем выражения для компонент напряжений и перемещений.

Случай вертикальной силы (рис. 4.29).

 

 

(4.81)

 

 

 

 

(4.82)

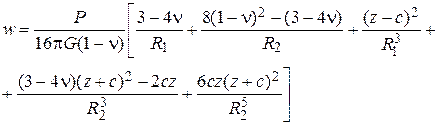
Случай горизонтальной силы (рис. 4.30).

 

Рисунок 4.30. - Схема к определению напряжений в основании в задаче Миндлина

для горизонтальной сосредоточенной силы

 

 

 

(4.83)

 

 

 

 

 

(4.84)

 

.

 

 

4.7. Практические методы расчета осадок оснований

 

Определение осадок методом послойного суммирования

В предыдущих разделах мы не раз обращались к величинам перемещений и осадок основания. Однако во всех случаях грунт предполагался однородным, что в реальных условиях встречается редко. В этом пункте приводится более универсальный метод расчета осадок линейно-деформируемого полупространства, который называется метод послойного суммирования. Метод послойного суммирования является приближенным, но, вместе с тем, он очень широко используется в практике проектирования при расчете деформаций оснований фундаментов. в этом методе приняты некоторые упрощения, например, при определении бытовых напряжений неоднородность основания учитывается, а при определении дополнительных - нет. Возможность бокового расширения грунта учитывается интегральным коэффициентом 0,8.

На рис. 4.31 показана расчетная схема основания и фундамента. Фундамент шириной b передает на основание давление p ₀, приложенное в уровне подошвы фундамента FL. Действие грунта, расположенного выше подошвы фундамента, заменяется эквивалентной пригрузкой , где d - глубина заложения фундамента от природного уровня рельефа NL. Построим координатную ось Oz, как показано на рис. 4.31. Деформации основания будут определяться для точек под центром фундамента.

 

Рисунок 4.31. - Схема к расчету осадок методом послойного суммирования

 

 

Приведем последовательность расчета.

1. Ниже подошвы фундамента основание разбивается на условные слои толщиной . При этом надо следить, чтобы границы условных слоев совпадали с границами реальных инженерно-геологических элементов. Заметим, что количество слоев пока не известно.

2. Определяем ту часть внешней нагрузки, действие которой будет вызывать деформирование грунта:

,

где - природное напряжение в уровне подошвы фундамента.

Это следует из принятой гипотезы: деформация основания не начинается до тех пор, пока внешняя нагрузка не превысит вес грунта, вынутый при разработке котлована.

3. Определяем бытовые напряжения в каждом i -ом слое с учетом природного напряжения в уровне подошвы

.

Здесь - координата центра тяжести i -ого слоя - удельный вес грунта, в котором находится i -ый слой. В результате строим эпюру бытовых напряжений, на рис. 4.31 она дана слева от оси Oz.

4. Определяем дополнительные напряжения в каждом i -ом слое, которые согласно решению Лява-Короткина равны

,

где - коэффициент рассеивания напряжений, определяемый согласно из (4.76), 2 l - длина фундамента.

5. Определяем мощность активной зоны сжатия. Понятно, что с глубиной вклад в общее напряженное состояние дополнительных напряжений по сравнению с бытовыми становится пренебрежимо мал (см. рис. 4.31). Поэтому осадку, рассчитываемую как раз от дополнительных напряжений, имеет смысл определять только в верхних слоях основания, где величина дополнительных напряжений существенна. Назначение такой глубины выполняют, исходя из эмпирических данных (Морозов, 1938). Считается, что для большинства грунтов рассмотрение напряженно-деформированного состояния основания не существенно, начиная с глубины, на которой выполняется условие

.

Расстояние от подошвы фундамента до указанной глубины называют мощностью активной зоны сжатия H_c, в пределах которой и вычисляют осадку.

6. В пределах указанной глубины - активной зоны сжатия - рассчитываем осадку каждого i -ого слоя грунта:

,

где E_i - модуль деформации грунта, в котором находится i -ый слой, b - коэффициент, учитывающий ограниченную возможность бокового расширения грунта аналогично коэффициенту b, рассмотренному в главе о компрессии, обычно принимают b = 0,8.

Заметим, что отношение есть относительная деформация i -го слоя, а представленное выражение - закон Гука.

7. Окончательно осадка определится по формуле:

,

где H_с под знаком суммы означает, что суммирование ведется в пределах активной зоны сжатия.

Представленная методика, таким образом, позволяет, хотя и приближенно, учитывать напластование грунтов с различной деформируемостью. Кроме того, используя метод угловых точек можно определять осадку в произвольной точке основания, а не только под центром и под краем, или легко учесть влияния соседних сооружений.

Особо следует подчеркнуть, что этот расчет можно выполнять, только если внешнее давление не превышает первой критической нагрузки и грунт работает в первой фазе деформирования по Н.М. Герсеванову - фазе уплотнения.

Расчетная схема линейно-деформируемого слоя конечной толщины.

Расчетная схема линейно-деформируемого слоя конечной толщины распространяется на случаи, когда в основании на некоторой глубине расположен практически несжимаемый грунт, например, скальная порода. Эту схему называют основанием с жестким подстилающим слоем. Расчет осадок такого основания производится преимущественно с использованием решений К.Е. Егорова.

Жесткий подстилающий слой приводит к изменению распределения сжимающих напряжений по глубине, а именно к концентрации напряжений, к более медленному их затуханию. Этот эффект тем больше, чем тоньше сжимаемый слой грунта. Поэтому влияние жесткого подстилающего слоя будет зависеть от отношения , где H - толщина сжимаемого слоя (или глубина расположения жесткого подстилающего слоя, a - полуширина прямоугольной или радиус круглой загруженной площади).

Приступая к определению осадки, вначале рассмотрим разность s вертикальных перемещений точек, лежащих на одной вертикали, но на различной глубине, определенную по теории линейно-деформируемого полупространства:

.

Выражение для w (z) можно представить в виде:

.

Величина зависит от формы загруженной площади, условий передачи нагрузки на основание и расположения вертикали, по которой находятся перемещения. Например, в частном случае, прямоугольной площади, загруженной равномерной вертикальной нагрузкой, величина для точек основания под ее углом определяется выражением в квадратных скобках в формуле (4.28):

Таким образом, выражение для осадки s (в данном случае разности вертикальных перемещений точек на глубинах z ₁ и z ₂) можно записать в виде:

Для осадок поверхности , относительно перемещения на некоторой глубине H , будем иметь:

Очевидно, что при расположении на глубине H несжимаемого грунта приведенная формула дает искомую абсолютную осадку поверхности основания. Если в пределах сжимаемой толщи H расположены грунты с различной сжимаемостью, характеризуемой параметрами деформируемости: E - модуль деформации и n - коэффициент Пуассона, то осадку этой толщи можно определить выражением:

В последнем выражении n - это число слоев с различными параметрами деформируемости, расположенные в пределах сжимаемой толщи мощностью H и имеющие кровлю на глубине z_{i -1} и подошву на глубине z_i.

Теперь перейдем к учету жесткого подстилающего слоя. Эффект концентрации напряжений, вызываемый его наличием, можно приближенно учесть с помощью коэффициента влияния M, введенного К.Е. Егоровым:

Значения коэффициента M приведены в таблице в зависимости от отношения глубины расположения жесткого подстилающего слоя .

 

Значения коэффициента M влияния жесткого подстилающего слоя

	0…0,5	0,5…1	1…2	2…3	3…5	>5
M	1,5	1,4	1,3	1,2	1,1	1,0

 

Данные приведенной таблицы наглядно показывают степень влияния жесткого подстилающего слоя в зависимости от глубины его залегания. Расчетная схема линейно-деформируемого слоя конечной толщины нашла широкое применение, например, для расчета осадок плитных фундаментов, ширина которых более 10 м.

 

4.8 Контактная задача

 

С точки зрения реальной работы оснований фундаментов граничные условия в ряде рассмотренных решений имеют один существенный недостаток, в частности, в решениях Мичелла и Лява-Короткина. Он заключается в том, что, прикладывая нагрузку к основанию, мы получали криволинейное очертание поверхности в месте приложения нагрузки (рис. 4.32, а). Следовательно фундамент в этих решениях не только получал осадку, а изгибался, причем изгиб полностью определялся деформацией основания, а в качестве осадки принимался максимальный «прогиб» линии подошвы фундамента.

 

 

Рисунок 4.32. - Схемы абсолютно жесткого, абсолютно гибкого и конечной

жесткости фундаментов

 

Реальные же фундаменты почти всегда имеют жесткость много выше жесткости основания, сложенного дисперсными грунтами. Это означает, что деформированный вид системы «основание-фундамент» будет ближе к показанному на рис. 4.32, б, в.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: