 |
Выражение (2.27) можно записать в виде 9 глава
|
|
|
|
Таким образом, можно выделить три типа фундаментов:
- абсолютно гибкий фундамент, когда деформированный вид линии подошвы фундамента следует за деформациями основания, т.е. нагрузка как бы состоит из отдельных несвязанных между собой элементарных сил (рис. 4.32, а);
- абсолютно жесткий фундамент, когда линия подошвы остается прямой после деформации (рис. 4.32, б);
- фундамент конечной жесткости, когда линия подошвы деформируется, но величина деформации определяется соотношением конечных жесткостей основания и фундамента (рис. 4.32, в).
Различие в деформированных схемах, несомненно, повлечет за собой и несовпадение напряженного состояния, особенно в местах приложения давления. В этой связи важно отметить следующее.
Согласно принципу Сен-Венана по мере удаления от места приложения нагрузки напряженное состояние все меньше зависит от способа передачи нагрузки на среду и определяется лишь величиной нагрузки. Поэтому приходим к важному выводу о корректности рассмотренных выше решений ТЛДС для задач определения напряженно-деформированного состояния основания в целом. Однако также очевидно, что в некоторой области основания, непосредственно примыкающей к загруженной границе, расхождения с реальной картиной напряженно-деформированного состояния основания будут уже существенными.
Указанная проблема обычно рассматривается в контактных задачах. Под контактной задачей понимают задачу определения давлений на границе контакта между двумя телами. В данном случае одним телом является фундамент, другим - грунтовое основание.
Знание контактных давлений необходимо при расчете фундамента на прочность и определении напряженно-деформированного состояния основания.
|
|
|
Рассмотрим вначале модель фундамента, а затем модели основания.
В постановке классической контактной задачи принимаются следующие гипотезы:
- для фундаментов применима гипотеза плоских сечений;
- внешнее воздействие на фундамент полностью уравновешивается реакцией грунта по подошве;
- грунт и фундамент деформируются совместно, т.е. отсутствует «отлипание» фундамента от основания;
- в рассматриваемых ниже решениях трением по подошве пренебрегаем, т.е. подошвы фундаментов считаем абсолютно гладкими.
Первая из данных гипотез обеспечивает правомерность применения уравнения изогнутой оси балки. Из курса Сопротивления материалов известно, что для балки в сечении с координатой x прогиб w (x), угол поворота сечения q(x), изгибающий момент M (x), перерезывающая сила Q (x) и распределенная нагрузка q (x), действующая на балку, связаны следующими дифференциальными соотношениями:
, (4.85)
где EI - постоянная по длине жесткость балки.
Вообще говоря, в рассматриваемой задаче мы имеем дело не с балкой, а с некоторой загруженной фундаментной лентой (полосой), работающей в условиях плоской деформации. Для такой полосы уравнения (4.85) также являются справедливыми с тем отличием, что вместо изгибной жесткости EI балки будем иметь цилиндрическую жесткость полосы фундамента:
, (4.86)
где EF и n F - модуль упругости и коэффициент Пуассона материла фундамента, IF - момент инерции поперечного сечения полосы фундамента.
Для случая, показанного на рис. 4.33, давление q (x) определится как
, (4.87)
где f (x) - внешняя нагрузка на полосу, как правило, заданная, p (x) - реакция по подошве полосы, как правило, искомая.
Рисунок 4.33. - Схема нагрузок на фундаментную полосу на основании
Тогда, с учетом (4.85)…(4.87) окончательно имеем
. (4.88)
В одно дифференциальное уравнение (4.88) входят две неизвестные функции w (x) и p (x). Следовательно, для получения решения необходимо записать дополнительные уравнения, связывающие осадку основания w (x) на границе контакта и искомую реакцию p (x).
|
|
|
Для описания работы основания используют две основные модели [10] - модель основания Фусса-Винклера (1801, 1867) и модель линейно-деформируемой среды.
Наглядно принципиальное отличие этих моделей продемонстрировано на рис. 4.34. Основное их отличие состоит в следующем. В модели линейно-деформируемой среды грунт деформируется не только в месте приложения нагрузки, но и на значительном расстоянии от нее (рис. 4.34, а). В модели Фусса-Винклера деформация предполагается только в местах приложения нагрузки (рис. 4.34, б). Считается, что первый случай лучше отвечает более прочным грунтам - песчаным и твердым глинистым грунтам, а второй более слабым - водонасыщенным глинистым.
Рисунок 4.34. - Схема линейно-деформируемого основания (а) и основания
Фусса-Винклера (б)
Подробней особенности данных моделей и вытекающие из них следствия рассмотрим далее.
4.8.1. Модель основания Фусса-Винклера
В основу данной модели положена следующая дополнительная гипотеза: грунт деформируется только в местах приложения нагрузки, причем в каждой точке осадка прямо пропорциональна величине давления (рис. 4.34, б):
, (4.89)
где k - коэффициент постели - величина, характеризующая деформационные свойства основания.
Эта гипотеза называется гипотезой коэффициента постели. Из (4.89) следует, что коэффициент постели численно равен давлению, вызывающему единичную осадку. Формула (4.89) дана для участка единичной длины в направлении оси Oy, как и ранее в случаях плоской деформации.
Подставляя (4.89) в уравнение изогнутой оси (4.88), имеем
, (4.90)
или
, (4.91)
где
.
Опуская вывод, сразу запишем интеграл данного уравнения, который обычно дается в виде:
,
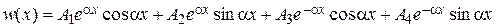или
. (4.92)
Здесь: A 1, A 2, A 3, A 4 - постоянные интегрирования, получаемые из граничных условий, Y 1, Y 2, Y 3, Y 4 - функции А.Н. Крылова, равные
, 
,
, 
,
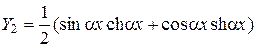где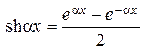 
и 
- гиперболические синус и косинус.
Приведем простое решение для частного случая, когда фундамент можно принять абсолютно жестким (рис. 4.35). Поскольку абсолютно жесткий фундамент не деформируется, то подошва после приложения нагрузки также остается прямой, и уравнение линии подошвы фундамента можно представить в виде:
|
|
|
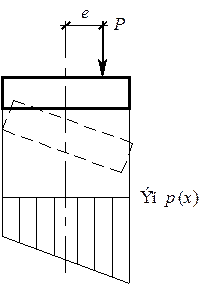
Рисунок 4.35. - Напряжение по подошве абсолютно жесткого фундамента
на основании Фусса-Винклера
,
где w 0 - осадка основания в точке x = 0, q - угол наклона подошвы к горизонту.
Согласно (4.89) напряжения по подошве равны
.
Полученную трапецеидальную эпюру напряжений можно представить в виде суммы эпюр - прямоугольной с равнодействующей 
и треугольной с равнодействующей 
, отстоящей от начала координат на b /6.
Составим уравнения равенства проекций всех сил на вертикальную ось и равновесия моментов относительно начала координат
;
,
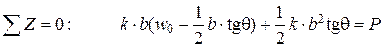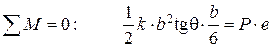где e - эксцентриситет приложения равнодействующей внешней нагрузки P.
Решая систему уравнений, имеем
.
С учетом полученного и (4.89), окончательно запишем
. (4.93)
Нетрудно убедиться, что полученное выражение совпадает с известной из Сопротивления материалов формулой для нормальных напряжений в прямоугольном сечении при внецентренном сжатии:
.
Действительно, P - продольная сила,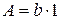 
- площадь сечения, 
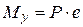- момент внешних сил в сечении, 
- момент инерции, x - расстояние от нейтральной оси до рассматриваемой точки.
Решая эту же задачу в пространстве можно вполне аналогично получить
. (4.94)
Заметим, что в приведенном простейшем случае, когда фундамент принимается абсолютно жестким, решение удалось получить, не прибегая к уравнению (4.92), которое используется в общем случае, когда рассматривается фундамент конечной жесткости.
4.8.2. Модель линейно-деформируемого основания
В данной модели при описании работы грунта справедливыми являются все гипотезы ТЛДС (см. п. 4.2.2). Как уже говорилось выше, осадка поверхности будет иметь место не только в точках приложения нагрузки, но и по всей границе основания (рис. 4.34, а).
В случае плоской задачи осадка w (x) поверхности в точке M (x) от силы P = 1, приложенной на расстоянии x от начала координат (рис. 4.36, а), будет функцией от аргумента 
:
.
Пусть на поверхности задана некоторая распределенная нагрузка p (x) (рис. 4.36, б), тогда осадка от элементарной силы 
составит
|
|
|
, (4.95)
Проинтегрировав выражение (4.95), получим осадку в рассматриваемой точке от всей нагрузки
Рисунок 4.36. - К определению перемещений точек поверхности от единичной силы (а)
и от распределенной нагрузки (б)
. (4.96)
С учетом полученного выражения уравнение изогнутой оси подошвы фундамента (4.88) примет вид:
. (4.97)
Используя формулу (4.50) для осадки поверхности в задаче Фламана
, (4.98)
перепишем (4.97) в виде
. (4.99)
Напомним, что помимо (4.99) искомая функция p (x) должна также удовлетворять уравнениям равновесия сил и моментов, которые в данном случае имеют вид:
; 
,
где P и M - равнодействующая и момент внешних сил.
Коротко рассмотрим результаты некоторых решений в предположении о бесконечно большой жесткости конструкции фундамента (рис. 4.37 а, б, в) [17].
Решение для центрально приложенной нагрузки было получено М. Садовским в 1928 г. (рис. 4.37, а):
, (4.100)
где a - половина ширины фундамента.
В.А. Флориным (1934г.) было дано решение для загружения жесткого фундамента парой сил (рис. 4.37, б):
Рисунок 4.37. - Напряжение по подошве абсолютно жесткого фундамента на линейно-деформируемом основании при различных схемах загружения; 1 - эпюра контактных напряжений, рассчитанных по теории линейно-деформируемой среды, 2, 3, 4 - трансформация фактической эпюры контактных напряжений при увеличении нагрузки
, (4.101)
где q - угол наклона подошвы, E и n - модуль деформации и коэффициент Пуассона основания.
Таким образом, при внецентренном загружении суммированием решений (4.100) и (4.101) получим:
. (4.102)
Все три решения обладают следующей особенностью. Как следует из формул (4.100)…(4.102), под краями фундаментов, т.е. при 
, напряжения равны бесконечности (рис. 4.37, а, б, в). Понятно, что напряжения не могут быть бесконечно большими, поскольку ограничены пределом текучести. Однако качественно полученные эпюры подтверждают тот факт, что разрушение действительно начинается под краями фундаментов.
Реальная эпюра контактного давления по указанной причине отличается от теоретической 1 и показана на рис. 4.37, а, пунктирной линией 2. Отметим, что трансформация реальной эпюры контактных давлений 2 - 3 - 4 продолжается вплоть до момента разрушения основания, когда она из седлообразной окончательно переходит в выпуклую.
Для фундаментов конечной жесткости выполненные исследования позволили сделать вывод о том, что величина и характер деформаций и напряжений в основании на границе с фундаментом будет определяться, главным образом, соотношением жесткостей грунта и фундамента.
На примере описанной задачи центрально нагруженного абсолютно жесткого фундамента рассмотрим численный метод решения контактной задачи, который в последствие можно обобщить на более сложные случаи.
|
|
|
Согласно (4.50), имеем
, (4.103)
где 
.
Поставим задачу: по заданной функции w (х) с помощью (4.103) определить функцию р (х). В последнем случае искомая функция входит под знак интеграла и равенство (4.103) превращается в интегральное уравнение. В рассматриваемом случае контактной задачи необходимо определить такой закон контактного давления, при котором в пределах подошвы фундамента осадка w (х) = w 0 = const. Для приближенного решения поставленной задачи заменим в (4.103) интегрирование суммированием по способу прямоугольников. С этой целью интервал [- a, a ] разобьем на n равных частей длиной h = 2 a / n. Осадку w (хi) и давление р (хi) для большей точности будем относить к срединным точкам этих частей, координаты хi которых определяются равенством
, i = 1, 2, …, n.
Ради удобства введем сокращенное обозначение
, 
, 
, j = 1, 2, …, n.
В результате осадку в точке с координатой х, при известном законе распределения давления р (хi) приближенно можно определить выражением
.
В контактной задаче, напротив, надо определить контактные давления p 1, p 2, …, pn. Используя предыдущую формулу, можно для этой цели записать систему n линейных уравнений:
 ,
| (4.104) |
где 
.
К системе (4.104) необходимо добавить уравнение равновесия фундамента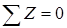 
:
 .
| (4.105) |
Система уравнений (4.104), (4.105) состоит из n + 1 линейных уравнений и содержит столько же неизвестных. К ним кроме известных давлений pi относится и величина s 0. Решение линейной системы не представляет сложности, в особенности если использовать ЭВМ. Полученная таким путем эпюра контактного давления имеет ступенчатый вид, как показано на рис. 4.38. Очевидно, решение задачи будет тем точнее, чем больше участков взято на контактной поверхности. При n ®¥ решение будет стремиться к точному решению (4.100), а эпюра контактного давления - к гладкой эпюре.
Рисунок 4.38. - К численному методу решения контактной задачи
4.9. Первая критическая нагрузка по проф. Н.П. Пузыревскому, 1923 г.
До сих пор при определении напряженного состояния основания мы не были ограничены величиной задаваемой нагрузки. Формально подставляя в приведенные выше формулы для напряжений сколь угодно большие нагрузки, можно было получать и сколь угодно большие значения напряжений. Ясно, что это не соответствует действительности.
Как следует из фактического характера работы грунта (см. п. 4.1 фазы деформирования по Н.М. Герсеванову), при превышении внешней нагрузкой значения первой критической, в грунтовом основании начинают интенсивно развиваться процессы пластического течения грунта. Поведение грунта уже не подчиняется закону Гука, а основанные на нем решения ТЛДС дают качественно неверные результаты, например, величины осадок основания оказываются сильно заниженными. Кроме того, в самой постановке задач ТЛДС отсутствуют какие-либо критерии, позволяющие оценить степень опасности нагрузки, степень близости напряженного состояния грунта к предельному.
Поставим задачу определить, при каком давлении p в основании начнут возникать области предельного напряженного состояния. Иначе говоря, вопрос заключается в теоретическом расчете величины первой критической нагрузки. Впервые эта задача была рассмотрена проф. Н.П. Пузыревским. Приводимое решение базируется на решении Мичелла и условии Кулона-Мора, при этом учитывается еще и бытовое напряженное состояние. Сказанное означает, что нагрузка на основание, а следовательно и напряжения, получаемые по ТЛДС, могут возрастать лишь пока не нарушается условие прочности.
Вначале рассмотрим соответствие между реальной и расчетной схемами аналогично тому, как это было сделано в п. 4.7.1. Фундаменты зданий и сооружений практически всегда заглубляются в основание на некоторую глубину d. При определении напряженно-деформированного состояния основания это заглубление может быть учтено приложением равномерного давления q = g d к расчетной поверхности основания, проведенной на уровне подошвы фундамента (рис. 4.39).
Рисунок 4.39. - Расчетная схема задачи Пузыревского об областях пластических деформаций в основании от равномерной полосовой нагрузки
Предположим, что фундамент шириной b = 2 a центрально загружен силой Р и создает равномерное давление на основание интенсивностью р 0 = Р / А (А - площадь подошвы фундамента). Часто фундамент имеет длину, во много раз превышающую его ширину. Теоретически допустимо считать такой фундамент бесконечно длинным и действие его на основание заменить равномерным полосовым давлением, т.е. приходим к условиям плоской деформации.
Заданную систему нагрузок на расчетную поверхность основания можно представить в виде суммы равномерного давления q, действующего на всей поверхности, и равномерного давления р = р 0 - q, приложенного в пределах ширины подошвы фундамента. Напряженное состояние в основании от указанной полосовой нагрузки определим с помощью формул Мичелла (4.56):
.
Другая часть напряжения возникает от сплошной равномерной пригрузки q и собственного веса грунта. В произвольной точке основания, расположенной на глубине z от его расчетной поверхности, эта часть напряжений согласно формулам (4.42) и (4.43) составит
, 
.
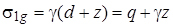Введем гипотезу x = 1, что отвечает значению коэффициента Пуассона n = 0,5. В результате получаем гидростатическое бытовое напряженное состояние, в котором все главные напряжения от собственного веса грунта в точке равны между собой
,
и в котором все площадки в точке являются главными. Это следует из того, что при таком напряженном состоянии круг Мора стягивается в точку и на любой площадке 
. В результате полные главные напряжения можно получить простым суммированием двух указанных частей:
 ,
 .
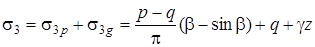| (4.106) |
Как было сказано выше, при некотором давлении фундамента в основании возникают области пластических деформаций, в которых напряжения достигают предела текучести грунта. Для того чтобы напряжения в какой-либо точке достигали предела текучести грунта, они должны удовлетворять условию текучести Кулона-Мора, которое запишем в главных напряжениях
.
Подставим (4.106) в условие Кулона-Мора. При этом учтем, что
, 
,
и тогда получим:
,
или
.
Отсюда выразим координату z:
 .
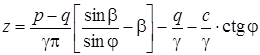| (4.107) |
В полученном равенстве z и b определяют точку, в которой имеет место предельное напряженное состояние. Можно определить совокупность таких точек при постоянном значении давления p. Указанная совокупность точек будет представлять собой границу области разрушения основания при данном p, т.е. на этой границе выполнятся условие Кулона-Мора (круг Мора касается прямой Кулона). В соседних с ней областях грунт либо еще находится в безопасном состоянии (круг Мора «внутри» прямой Кулона), либо будет уже разрушен, поскольку круг Мора здесь пересечет прямую Кулона (рис. 4.39).
Остановимся подробней на геометрии границы зон разрушения. Чтобы получить уравнение, определяющее эти границы, к равенству (4.107) необходимо добавить еще одно выражение, которое связывало бы вторую координату х с углом b. Такое выражение можно получить исходя из первого равенства (4.54). Запишем его, используя известное тригонометрическое выражение, в виде
.
Учитывая, что
, 
,
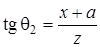получим
.
Отсюда установим искомую зависимость, выразив координату x:
 .
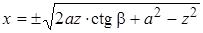| (4.108) |
Равенства (4.107), (4.108) в совокупности представляют собой параметрическую форму уравнения границ областей пластических деформаций, параметром которого является угол b в интервале 0 £ b £ p.
Исследования уравнений (4.107), (4.108) показывают, что когда фундамент заглублен в основание или расположен на поверхности связного грунта (
), области пластических деформаций имеют замкнутый вид. Правая область такой формы показана на рис. 4.40 под номером 1. В случае, когда фундамент располагается на поверхности (q = 0) сыпучего (c = 0) основания, области пластических деформаций оказываются разомкнутыми, выходящими на поверхность основания. Правая область такой формы представлена на рис. 4.40 под номером 2.
Рисунок 4.40. - Замкнутая 1 и разомкнутая 2 области пластических деформаций
С практической точки зрения нас, прежде всего, будет интересовать максимальная глубина их развития z max (см. рис. 4.39). Для определения этой величины поступим согласно общему правилу отыскания экстремума функции. Возьмем производную от (4.107) по b и приравняем ее нулю:
.
Отсюда, поскольку 
, должно равняться нулю выражение, заключенное в скобки. В результате получаем равенство 
, из которого следует
 .
| (4.109) |
Подставив это выражение в (4.107), получим формулу для максимальной глубины развития пластических деформаций
 .
| (4.110) |
Полученное уравнение решим относительно внешней нагрузки:
 .
| (4.111) |
Если в (4.111) положить 
, то получим такое значение нагрузки, при котором впервые начинается разрушение грунта:
 .
| (4.112) |
Выражение определяет (4.112) совершенно безопасное давление на основание, или первую критическую нагрузку по Н.П. Пузыревскому.
Из выражения (4.112) предельным переходом при j ® 0 получим формулу первого критического давления на основание, сложенное идеально связанным грунтом (
):
|
|
|
