 |
Выражение (2.27) можно записать в виде 10 глава
|
|
|
|
 .
|
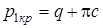Последующие исследования показали, что в общем случае первая критическая нагрузка, рассчитанная по формуле (4.112), занижает наблюдаемое в опытах значение. Поэтому в практике проектирования оснований и фундаментов используют не совершенно безопасное давление (4.112), а нагрузку, рассчитываемую по формуле (4.111) при z max = b / 4, т.е. допускают развитие областей пластических деформаций на глубину в четверть ширины фундамента (рис. 4.39) [25]:
 .
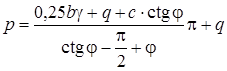| (4.113) |
В нормах проектирования фундаментов эта величина используется для определения очень важной характеристики - расчетного сопротивления R грунта основания, по которому преимущественно рассчитываются размеры подошвы фундаментов промышленных и гражданских зданий. Обычно для расчетного сопротивления записывают в виде:
 .
| (4.113) |
где M g, Mq, Mc - коэффициенты, зависящие от угла внутреннего трения:
, 
, 
.
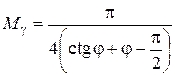Отметим две особенности изложенного решения.
Первая особенность заключается в принятии равенства x = 1 для определения природного напряженного состояния основания, тогда как в действительности коэффициент бокового давления должен быть меньше единицы, а коэффициент Пуассона меньше 0,5. Эта неточность в значительной мере оправдывается тем, что природное напряженное состояние внутри небольших по размерам областей пластических деформаций составляет лишь часть, притом меньшую, общих напряжений. Принятие же в расчет напряжений, определенных как для условий компрессионного сжатия, т.е. n < 0,5, при углах внутреннего трения 
приводит к нарушению условия прочности даже без внешней нагрузки, а только от действия собственного веса. В этом можно убедиться, подставив выражения (4.42) и (4.43) при q = 0 в условие Кулона-Мора.
|
|
|
Вторая особенность состоит в том, что внутри областей пластических деформаций напряжения превышают предел текучести грунта (¦ > 0, ¦ - функция пластичности), чего, во-первых, не должно быть в действительности (¦ £ 0 - всюду), а во-вторых, если это так, то решения ТЛДС неприменимы. Указанная некорректность, очевидно, тем меньше, чем меньше размеры областей пластических деформаций.
Учитывая рассмотренную нестрогость решения, в практическом его использовании считаются допустимыми области пластических деформаций, удовлетворяющие неравенству 
.
5. Теория устойчивости грунтовых массивов
5.1 Задачи и методы теории устойчивости
5.1.1. Основные задачи теории устойчивости
Момент разрушения основания принято называть потерей устойчивости или исчерпанием его несущей способности. Разрушение основания происходит, главным образом, за счет сдвигов и выражается в быстром нарастании деформаций, вызванных пластическим течением грунта.
Любое безопасное состояние грунта, как угодно удаленное от предельного, будем называть устойчивым.
Основной предмет исследований теории устойчивости - разрушение грунта. Ранее мы иллюстрировали физическую суть данного явления на примере основания штампа в момент выпирания грунта из-под подошвы по некоторым поверхностям скольжения (см. п. 4.1). Сходные по существу процессы происходят и в других случаях. Оползневые явления с механической точки зрения представляют собой сдвиг или скольжение оползневого массива по несмещающимся породам. Давление грунта на подпорные сооружения также определяется силовым взаимодействием неподвижной грунтовой области и некоторого объема грунта, непосредственно примыкающего к сооружению и стремящегося обрушиться по определенной поверхности.
Таким образом, выделяют три основные задачи теории устойчивости:
|
|
|
- задача о несущей способности основания;
- задача определения устойчивости откосов и склонов;
- задача о предельном давлении грунта на ограждающие сооружения.
Задача о несущей способности основания. Обратимся еще раз к опыту со штампом, моделирующему работу основания реального фундамента Напомним основные моменты, имеющие отношение к устойчивости, и уточним терминологию.
Итак, при некоторой нагрузке на штамп Pu и соответствующем давлении pu достигается предел, который называют несущей способностью основания. Под несущей способностью обычно понимают силу, а не напряжения. Силу Pu и давление pu называют предельными. В опыте им соответствует вторая критическая нагрузка.
При нагрузках P < Pu говорят, что основание устойчиво, а при P = Pu оно переходит в состояние предельного равновесия, при котором сколь угодно малое увеличение нагрузки приведет к потере устойчивости основания. Схема потери устойчивости основания штампа (фундамента) дана на рис. 5.1. Стрелками обозначено направление пластического течения объема грунта по поверхностям скольжения и скорость v, с которой штамп непрерывно погружается в основание.
Равенство P = Pu означает, что в областях пластического течения напряжения достигли предела прочности (предела текучести) грунта, т.е.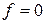 
, ¦ - функция текучести, в нашем случае закон Кулона-Мора. Иначе говоря, в этих областях грунт находится в предельном напряженном состоянии или в состоянии предельного равновесия.
Рисунок 5.1. - Задача о несущей способности
Задача о несущей способности заключается в определении предельной нагрузки на основание:
 ,
| (5.1) |
где j, c и g - прочностные характеристики и удельный вес грунта, b - ширина штампа (фундамента).
Задача определения устойчивости откосов и склонов. Необходимость определения устойчивости откосов и склонов возникает при оползневых процессах, возведении и эксплуатации откосов насыпей и выемок, строительстве на склонах или в непосредственной близости от них (рис. 5.2). В последнем случае устойчивость основания сооружения зачастую определяется устойчивостью откоса, при этом его обрушение может произойти при нагрузке меньшей, чем предельная для такого основания, если оно горизонтально.
|
|
|
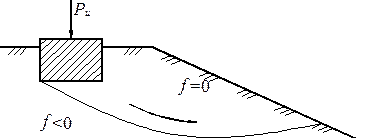
Рисунок 5.2. - Задача об устойчивости склонов
В похожих условиях находится насыпь земляного полотна железной дороги. Разница состоит только в том, что давление фундамента в этом случае заменяется нагрузкой от верхнего строения пути и подвижного состава.
Кроме характеристик грунта и величины внешней нагрузки (если она есть), в этом классе задач важными факторами являются очертание склона, его крутизна и геологическое строение - характер напластования грунтов. При неблагоприятных условиях, таких как малая прочность грунтов, большая крутизна склона, наличие слоя слабого водонасыщенного глинистого грунта, активно развиваются оползневые процессы.
Потеря устойчивости в перечисленных случаях выражается в смещении оползневого массива по некоторой поверхности скольжения относительно несмещающихся пород. Грунт можно считать предельно напряженным в оползневом массиве или хотя бы по поверхности скольжения, в несмещающейся части основания предельное состояние отсутствует.
Устойчивость откосов и склонов традиционно оценивается величиной, называемой коэффициентом устойчивости:
 ,
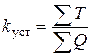| (5.2) |
где S T - сумма силовых удерживающих факторов (сил или моментов); S Q - сумма соответствующих сдвигающих факторов.
Говорят, что если 
, то склон устойчив, если 
, то произойдет обрушение, если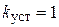 
, то грунт теоретически должен находится в предельном равновесии.
Задача о давлении грунта на ограждающие сооружения. В строительной практике часто прибегают к устройству различных ограждающих подпорных сооружений (рис. 5.3). Под действием разницы давлений грунта, расположённого за стенкой и перед стенкой, может произойти потеря устойчивости стенки в форме поступательного смещения или опрокидывания вокруг ребра A. При этом за стенкой образуется призма обрушения, а перед стенкой призма выпора грунта, в пределах которых грунт находится в предельном напряженном состоянии. Со стороны призмы обрушения на стенку действует активное давление грунта s a, со стороны призмы выпора - пассивное давление s p:
|
|
|
Рисунок 5.3. - Задача о предельном давлении на стенку
 ,
| (5.3) |
где h и b условно обозначают соответственно размеры подпорной конструкции и геометрию склона или основания по обе стороны от стенки.
Величины активного и пассивного давлений необходимы для правильного расчета прочности и устойчивости подпорного сооружения.
5.1.2. О методах решения задач теории устойчивости
В теории устойчивости грунтовых массивов используются различные модели грунта, принципы построения расчетных схем и методы решения конкретных задач. По существу, теорию устойчивости можно оформить в виде двух крупных направлений: теория предельного равновесия грунтов (ТПРГ) и приближенные методы расчета устойчивости.
Теория предельного равновесия грунтов является главной теоретической базой для определения предельной нагрузки. Она представляет собой систему строгих решений, объединенных общей постановкой задач и тесно связанных с математической теорией пластичности.
Основная область практического применения решений ТПРГ - задачи о несущей способности основания. Поэтому ТПРГ и задача о несущей способности будут объединены в одну главу. Получены также решения ТПРГ задач о предельном очертании склона, о предельном давлении на бровке откоса и некоторых других. Эти решения будут нами рассмотрены в соответствующих параграфах.
К сожалению, классические решения ТПРГ накладывают порой существенные ограничения на расчетные схемы - однородность и изотропность среды, упрощенность геометрии границ основания. По этой причине в задачах устойчивости откосов и склонов и определения предельного давления грунта на ограждения широко используют приближенные методы теории устойчивости.
Вместе с тем, ясность исходных положений и строгость теоретического обоснования результата заставляют отдавать предпочтение решениям ТПРГ перед результатами решений этих же задач, но полученных каким-либо иным способом.
Приближенные методы расчета устойчивости используются в случаях, когда применение строгих решений ТПРГ затруднено или невозможно.
Приближенные методы можно разделить на две группы. В первой группе методов вводятся какие-либо упрощения или допущения в строгие решения ТПРГ. В методах второй группы поступают следующим образом. Некоторой выбранной поверхностью, которая, как заранее полагают, должна быть поверхностью скольжения, выделяют в грунтовом массиве область обрушения. Полученную область разбивают на условные отсеки конечных размеров. Далее рассматривают силовое воздействие на каждый из них, но при этом напряженное состояние внутри отсеков не исследуется. Главные проблемы этих методов - неопределенность формы поверхности скольжения и неопределенность силового взаимодействия между отсеками. Это преодолевается посредством принятия ряда допущений относительно указанных проблем. Как следствие, данное направление теории устойчивости характеризуется большим количеством дополнительных гипотез, вводимых в расчет.
|
|
|
Несмотря на очевидную нестрогость, некоторые приближенные методы расчета получили многолетнюю апробацию на практике, во многих случаях являются единственно возможными, а их главным достоинством является простота, с какой можно учесть неоднородность грунтового массива и сложное очертание поверхности.
5.2 Теория предельного равновесия грунтов. Несущая способность оснований
5.2.1. Основные гипотезы плоской задачи ТПРГ
В настоящем учебнике в основном рассматриваются плоские задачи теории предельного равновесия грунтов (ТПРГ) [27, 29]. Строгие пространственные решения были получены только для частного случая - осесимметричного напряженного состояния, при котором напряжения распределяются симметрично относительно некоторой оси [3]. Кратко основы этих решений изложены в п. 5.2.6.
Перечислим основные гипотезы плоской задачи ТПРГ.
6. Основание находится в равновесии. Как и в теории линейно-деформируемой среды, необходимость введения этой гипотезы очевидна.
7. Каждая точка грунта в рассматриваемой области находится в предельном напряженном состоянии, т.е. напряжения отвечают закону Кулона-Мора. Поведение грунта при разрушении действительно свидетельствует о его предельном состоянии, а главное - разрушение происходит в виде сдвига, который лучше всего описывается законом Кулона, следовательно, и условием прочности Кулона-Мора. И хотя экспериментально установлено, что в момент разрушения не все точки грунта выходят в предельное состояние, и в опыте, и на практике было доказано, что принятие данной гипотезы обеспечивает получение вполне приемлемых результатов.
8. Деформации грунта не рассматриваются. Сразу оговоримся, что в более общих постановках ТПРГ большую роль играют скорости деформаций - так называемая кинематическая сторона или кинематический метод ТПРГ. Однако ниже будет рассматриваться только статический метод ТПРГ, в котором деформации среды отсутствуют в силу чисто математических особенностей постановки задачи. По этой причине иногда говорят, что плоская задача ТПРГ является статически определимой [21].
9. Грунт рассматривается как сплошное, однородное и изотропное тело. Отказ от этой гипотезы связан с трудностями, прежде всего, математического характера. Работ по анизотропии пластического течения грунта, как и по многослойному предельно напряженному основанию, сравнительно мало, и эта проблема находится в стадии разработки.
5.2.2. Постановка плоской задачи
При решении задач о напряженном состоянии грунтовой среды в равновесии должно находиться не только все основание в целом согласно гипотезе 1, но и каждая его частица. Это означает, что в любой точке грунта должны удовлетворяться дифференциальные уравнения равновесия бесконечно малого элемента (4.3) или (4.15), (4.29). Однако, как уже указывалось в п. 4.2.3, одних только уравнений равновесия недостаточно для того, чтобы однозначно определить напряженное состояние тела, поскольку в уравнениях равновесия число неизвестных превышает число уравнений (в два уравнения входит три неизвестных функции 
. Поэтому к уравнениям равновесия необходимо добавить еще одно уравнение, связывающее компоненты напряжения и выражающее физическую суть теории. Согласно гипотезе 2 в теории предельного равновесия грунтов таким уравнением, очевидно, должно быть уравнение предельного напряженного состояния грунта 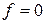. Таким образом, определяющая система уравнений теории предельного равновесия грунтов в прямоугольной системе координат 
будет:
в прямоугольной системе координат
 ;
| (5.4) |
Запишем исходную систему уравнений (5.4) в несколько ином виде, который удобно использовать в некоторых случаях:
 ;
 ;
 ;
| (5.5) |
Здесь 
означают приведенные компоненты нормальных напряжений:
(5.6)
где 
- временное сопротивление всестороннему равномерному растяжению.
В решениях ТПРГ использование приведенных напряжений бывает очень удобным. Этот искусственный прием означает перенос на диаграмме Мора оси O t на величину влево. Таким образом, в процессе решения задач удельное сцепление условно зануляется, и прочность грунта характеризуется только одним параметром - углом внутреннего трения j. С помощью указанных формул перехода всегда можно приведенные значения напряжений пересчитать в действительные.
Заметим, что переход от уравнений равновесия и условия прочности (5.4), записанных в действительных напряжениях, к уравнениям (5.5), записанным в приведенных нормальных напряжениях, производится простой заменой нормальных напряжений на приведенные нормальные напряжения, поскольку, например:
. (5.7)
Сделаем еще одно замечание по терминологии. При изложении решений задач ТПРГ мы будем пользоваться следующей классификацией оснований, предложенной автором этой теории В.В. Соколовским [ ]:
- невесомый сыпучий основание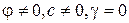 
;
- весомый идеально-связный основание 
;
- весомый идеально-сыпучий основание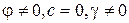 
;
- весомый сыпучий основание 
.
5.2.3. Каноническая система уравнений плоской задачи ТПРГ
Для решения конкретных задач, как правило, используется каноническая система уравнений, получаемая из исходной путем ряда преобразований. Полный вывод системы уравнений канонического вида весьма громоздок, поэтому приведем лишь основные этапы преобразований с соответствующими пояснениями, руководствуясь которым можно проверить справедливость предлагаемых выводов самостоятельно.
Прежде всего, введем две новые переменные: s - приведенное среднее напряжение, a - угол между осью Oz и направлением первого главного напряжения s1 (рис. 5.4). Тогда компоненты напряжений определятся формулами:
 ,
 ,
| (5.8) |
Рисунок 5.4. - Схема к понятию a и s
Среднее приведенное напряжение здесь и далее будем обозначать не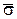 
, а просто s без черты. Новые переменные s и a можно выразить через напряжения следующим образом:
 ,  .
| (5.9) |
Важно, что подстановка (5.8) в условие прочности Кулона-Мора (последнее уравнение в (5.4)), тождественно ему удовлетворяет.
Подставим (5.8) в уравнения равновесия (5.4), предварительно выполнив дифференцирование
 ;
 ;
 ;
 .
| (5.10) |
Коэффициенты Aij введены для краткости дальнейшего изложения.
В результате получим основную систему уравнений
;
,
или, применяя коэффициенты Aij по (5.10),
 ;
 .
| (5.11) |
Заметим, что термин «основная» применяют и к другим видам системы (5.11).
Итак, решение плоской задачи ТПРГ будет сводиться к решению двух дифференциальных уравнений (5.11), содержащих две неизвестные функции a и s координат x и z. Если эти функции будут найдены, то по формулам (5.8) определятся все компоненты напряжений. Аналогичную в известной степени роль играет функция Эри в ТЛДС.
Уравнения (5.11) содержат четыре неизвестных частных производных функций a и s. Уменьшим их количество до двух. Из выражений для полных дифференциалов
 ,  ,
|
имеем
 ,  .
| (5.12) |
Теперь умножим оба уравнения (5.11) на dx и подставим в них (5.12). Результат запишем в виде
 ;
 .
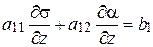| (5.13) |
В уравнениях (5.13):
 ,
 ,
 ;
|  ,
 ,
 .
| (5.14) |
Выражения (5.13), как и (5.11), с математической точки зрения представляют собой систему квазилинейных дифференциальных уравнений в частных производных первого порядка гиперболического типа. Опуская строгое математическое обоснование, скажем лишь, что решение системы (5.13) или (5.11) обычно сводят к решению обыкновенных дифференциальных уравнений первого порядка, называемых каноническими уравнениями, которые мы определим по следующей методике.
Решая систему (5.13) методом Крамера относительно производных, имеем
 ;
 .
| (5.15) |
Если знаменатель и числитель в (5.15) будут отличны от нуля, то производные 
и 
определятся единственным образом. Если только знаменатель равен нулю, то система несовместна. Этот особый случай, приводящий к понятию линий разрыва, нами рассматриваться не будет. Искомое решение получают, когда и числитель, и знаменатель приравнивают нулю одновременно. В этом случае значения производных и будут иметь бесконечное количество решений вдоль некоторых линий, уравнения которых и получаются из равенства нулю знаменателя и числителя. Такие линии в теории дифференциальных уравнений называются характеристиками.
Обратим внимание на то, что числители (5.15) содержат дифференциалы всех переменных 
, в то время как знаменатели - только dz и dx (5.14). Тогда приравнивая нулю знаменатель
 ,
|
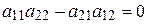имеем квадратное уравнение относительно производных 
. Решая его с учетом (5.10) и (5.14), выполнив необходимые преобразования, получим дифференциальные уравнения характеристик
 ,  .
| (5.16) |
Напомним физический смысл параметра m - это угол между направлением первого главного напряжения s1 и линиями скольжения (рис. 5.4). А поскольку a - угол наклона s1 к Oz делаем важный вывод о том, что характеристики совпадают с линиями скольжения.
Затем, подставляя полученные выражения в числители (5.15), также приравненные нулю, например,
 ,
|
получим дифференциальный закон изменения параметров a и s вдоль характеристик (линий скольжения)
 .
| (5.17) |
Особенность системы (5.15) такова, что, если 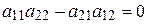, то корни уравнений и 
совпадают, в чем можно убедиться с помощью (5.10) и (5.14). Заметим также, что если систему (5.11) решить относительно другой пары производных - 
и 
, то в результате получим то же самое.
По характеристикам полностью выполняется исходная система уравнений (5.4), а их построение дает искомое поле предельных напряжений. Окончательно каноническая система уравнений статического метода ТПРГ примет вид:
| , ,
.
| (5.18) |
Систему (5.18) еще называют канонической системой уравнений статики сыпучей среды.
|
|
|
