 |
Выражение (2.27) можно записать в виде 11 глава
|
|
|
|
Как было показано в главе 3 и как следует из первого уравнения (5.18), через точку предельно напряженного грунта, проходят две линии скольжения, образуя угол 2m (рис. 5.4). Согласно сказанному в уравнениях (5.18) верхние знаки отвечают линиям скольжения 1-го семейства, а нижние знаки - линиям скольжения 2-го семейства.
Решение канонической системы (5.18) редко удается получить в аналитическом виде, поэтому в общем случае, как правило, прибегают к численному интегрированию, которое будет нами рассмотрено позже в п. 7.1. В этой главе приведем несколько простых решений в замкнутом виде, а при необходимости будем делать ссылки на указанный п. 7.1.
5.2.4. Области простейших предельных состояний грунта
Здесь разберем области простейших предельных состояний грунта, из которых в дальнейшем будем составлять решения практически важных задач. Некоторые замкнутые решения можно получить непосредственно из исходных уравнений (5.4)…(5.7), для других удобнее использовать канонические уравнения (5.16).
Вначале рассмотрим предельные напряженные состояния грунта в области, ограниченной сверху плоскостью, к которой приложено равномерное распределенное давление (рис. 5.5, а, б). Ось Oz совпадает с направлением силы тяжести. Далее, поскольку на поверхности z = 0 касательные напряжения 
отсутствуют, можно предположить, что в силу симметрии расчетной схемы они равны нулю и внутри основания. Поэтому 
являются главными напряжениями. Кроме того, так как граничные условия на поверхности основания не зависят от координаты х, естественно предположить, что и внутри основания напряжения не зависят от этой координаты, поэтому 
. Вследствие сказанного второе уравнение из системы (5.6) тождественно обращается в нуль, а оставшаяся часть принимает очень простой вид:
|
|
|
Рисунок 5.5. - Минимальное (а) и максимальное (б) напряженное состояние
 .
| (5.19) |
Частная производная 
заменена здесь на простую производную 
потому, что в рассматриваемом случае напряжение оказалось функцией только одного переменного 
.
Напряжение 
определим, проинтегрировав первое из уравнений (5.17), а напряжение 
выразим из второго уравнения:
 ,
| (5.20) |
или в действительных значениях
 ,
| (5.21) |
где 
- постоянные интегрирования. Очевидно, что 
.
Таким образом, мы имеем два решения и соответственно два вида предельных напряженных состояния грунта.
Минимальное напряженное состояние. Минимальным напряженным состоянием грунта называют предельное напряженное состояние (рис. 5.5, а), отвечающее верхним знакам в (5.18). Если для этого случая давление на поверхность основания обозначить буквой p, приведенное давление соответственно будет равно 
, то согласно (5.18) при 
имеем
 ,
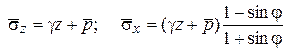| (5.22) |
приведенное среднее напряжение соответственно будет
 ,
| (5.23) |
Поскольку = 0, то 
и 
являются главными напряжениями. При этом из формул (5.19) видно, что есть наибольшее 
, а - наименьшее 
главные напряжения. Обращаясь к понятию о площадках и линиях скольжения, можем заключить, что через каждую точку области минимального напряженного состояния проходят две площадки и соответственно две линии скольжения, составляющие с направлением оси O (с направлением ) углы 
. В результате сетка линий скольжения (рис. 5.5, а) образована прямыми, наклоненными к оси Oz под углом 
(первое семейство) и углом 
(второе семейство линий скольжения). При ограниченной ширине полосы загружения О ' О область минимального напряженного состояния представляет собой треугольник О ' ОС, ограниченный крайними линиями скольжения первого и второго семейств, проходящими через края полосы загружения.
|
|
|
Максимальное напряженное состояние. Максимальным напряженным состоянием грунта называют предельное напряженное состояние грунта (рис. 5.5, б), отвечающее нижним знакам в (5.18). Если для этого случая приведенное давление на поверхность основания обозначить символом 
, что соответствует действительному давлению q, то согласно (5.18) на поверхности основания при 
должно выполняться граничное условие 
и мы имеем
 ,
| (5.24) |
а приведенное среднее напряжение будет
 .
| (5.25) |
Вследствие того, что = 0, напряжения и являются главными, причем из формул (5.21) видно, что - наименьшее, а - наибольшее из них. Поэтому площадки и линии скольжения в каждой точке области максимального напряженного состояния грунта составляют с осью Oх (с направлением 
) углы ± 
. В результате образуется сетка линий скольжения, в которой первое семейство линий наклонено к оси х под углом , а второе - под углом . При ограниченной ширине полосы загружения ОА область максимального напряженного состояния ограничивается треугольником ОАВ, образованным крайними линиями скольжения первого и второго семейства, проходящими через края полосы загружения (см. рис. 5.5, б).
Область переходного предельного состояния в невесомом основании. Рассмотрим теперь так называемую область переходного предельного состояния или зону радиального веера в невесомом грунте (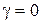
). Определим предельное напряженное состояние грунта в области ОВС (рис. 5.6, а), в которой первое семейство линий скольжения представлено отрезками прямых 
, исходящими из точки O (такую точку называют особой). По общему свойству линий скольжения второе семейство должно состоять из кривых, пересекающих радиальные прямые под постоянным углом 
.
Рисунок 5.6. - Область радиального веера
Согласно рис. 5.6, б, дифференциальное уравнение таких кривых имеет вид:
 ,
| (5.26) |
Проинтегрировав его, получим
 ,
| (5.27) |
где 
- начальный радиус кривой при значении угла q = q0.
Отсюда
 ,
| (5.28) |
и окончательно получаем
 .
| (5.29) |
Известно, что это уравнение логарифмической спирали. Именно логарифмическая спираль пересекает свои радиусы-векторы под постоянным углом, частным случаем которой является окружность, когда этот угол равен 
.
|
|
|
Описанная сетка линий скольжения может иметь место в невесомом грунте ().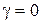
Пренебрежение влиянием собственного веса на предельное напряженное состояние грунта допустимо, если вес области ОВС пренебрежимо мал в сравнении с силами, действующими на ее границах. При прочих равных условиях указанное допущение тем меньше сказывается на точности решения задачи, чем меньше размеры области. В самом деле, если за характерный размер области принять, например, длину границы ОВ - отрезок 
, то длины остальных границ ВС и ОС, а вместе с ними и величины граничных сил будут пропорциональны . В то же время площадь и вес области, очевидно, пропорциональны 
. Поэтому, если уменьшается в n раз, то и граничные силы уменьшаются в n раз, тогда как вес области уменьшается в n 2 раз. Следовательно, при 
вес области становится пренебрежимо малым в сравнении с граничными силами. В результате в бесконечно малой окрестности точки О решение для невесомого грунта становится строгим. Как будет видно из дальнейшего, оно необходимо для получения приближенного решения во всей переходной области ОВС, имеющей конечные размеры.
Определим предельное напряженное состояние в области. Второе уравнение канонической системы (5.16) при 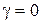примет вид:
 .
| (5.30) |
Выбирая здесь верхний знак, отвечающий 1-му семейству характеристик (рис. 5.6, а), вдоль которого производится интегрирование, имеем:
, 
,
, 
,
 .
| (5.31) |
Из (5.31) следует, что напряжения в области переходного напряженного состояния не зависят от радиуса.
Области простейших напряженных состояний в идеально-связном грунте. Одна из особенностей техники решения задач для идеально-связной среды (j = 0) состоит в том, что здесь нельзя использовать приведенные напряжения, поскольку 
. Условие прочности Кулона-Мора для идеально-связной среды запишется в виде
 или 
| (5.32) |
Уравнения (5.32) еще называют условием прочности Треска. Его широко используют в расчетах строительных конструкций.
Компоненты предельных напряжений даются равенствами:
|
|
|
 ,
| (5.33) |
где 
- среднее напряжение (не приведенное).
Рассмотрим области минимального (рис. 5.7, а) и максимального (рис. 5.7, б) напряженного состояния. Как и ранее касательных напряжений на границе основания нет, поэтому с учетом того, что 
являются главными напряжениями, причем s x не зависит от x, и с учетом (5.32) исходная система (5.4) примет вид
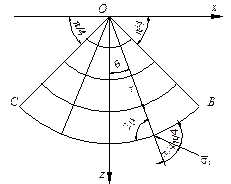
Рисунок 5.7. - Простейшие виды напряженных состояний в идеально-связной среде
 .
| (5.34) |
Интегралы этой системы для граничных условий, показанных на рис. 5.7, а, б, имеют вид:
для минимального напряженного состояния
| (5.35) |
для максимального напряженного состояния
| (5.36) |
Тогда среднее напряжение для минимального напряженного состояния определится как
 ,
| (5.37) |
для максимального напряженного состояния
 .
| (5.38) |
Угол между характеристиками двух семейств 
(так как 
), т.е. они всегда пересекаются под прямым углом (рис. 5.7, а, б).
Итак, области максимального и минимального напряженного состояния представлены прямоугольными равнобедренными треугольниками (рис. 5.7, а, б).
Далее, каноническая система уравнений (5.16) для идеально-связной среды имеет вид:
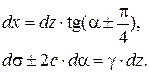
| (5.39) |
Чтобы это показать, распишем из второго уравнения (5.16)
слагаемое, содержащее среднее приведенное напряжение
.
Следует помнить, что хотя среднее напряжение для идеально-связной среды и среднее приведенное напряжение для сыпучей среды обозначаются одним символом s, определяются они по-разному.
Обычно при решении задач о предельном равновесии идеально-связной среды вводят следующую подстановку:
(5.40)
Тогда каноническая система уравнений для идеально-связной среды примет вид:
(5.41)
В переходной области также, как и для невесомой сыпучей среды, можно выделить семейство характеристик, представляющих собой пучок прямых, выходящих из особой точки O, и семейство кривых, пересекающих прямые под постоянным углом 2m = 90° (рис. 5.7, в). Их уравнение согласно (5.23)
 .
| (5.42) |
т.е. первое семейство представлено окружностями, с центром особой точке O.
Проинтегрируем второе уравнение (5.41) вдоль характеристик 1-го семейства
,
откуда
 .
| (5.43) |
Здесь s 0 и a0 - определяются граничными условиями.
5.2.5. Несущая способность оснований (задача Прандтля, 1920 г.)
Предельное давление на невесомое основание. Полученные в п. 5.2.4 результаты позволяют решить ряд задач теории предельного равновесия грунтов в аналитическом виде при условии, что можно пренебречь влиянием собственного веса грунта или внутренним трением. Одни из таких решений - решения Л. Прандтля задач о предельном давлении на невесомое и идеально-связное основание.
|
|
|
Ограничимся случаем симметричной задачи, когда фундамент загружен центральной сосредоточенной силой и с обеих сторон от него на основание действует равномерное давление q (рис. 5.8). Это давление проявляется за счет веса слоя грунта толщиной d, расположенного выше подошвы фундамента. Его действительная величина определяется выражением 
, где d - глубина заложения фундамента, а приведенная 
. Необходимо установить предельную величину давления фундамента на основание pu.
Рисунок 5.8. - К определению несущей способности невесомого основания
Область предельного напряженного состояния основания с сеткой линий скольжения показана на рис. 5.8. Она состоит из области минимального напряженного состояния О ¢ ОС, двух симметрично расположенных областей переходного напряженного состояния ОВС, О ¢ СВ ¢ и двух симметричных областей максимального напряженного состояния ОАВ, О ¢ В ¢ А ¢. Напряженное состояние в этих областях описано выше. Остается только объединить эти результаты так, чтобы получилось общее непрерывное поле предельных напряжений. Непрерывность напряжений будет соблюдена, если непрерывным будет приведенное среднее напряжение s на границах ОВ и ОС между соответственными областями. Речь идет только о правой половине общей области предельного непрерывного состояния грунта. Левая половина является зеркальным отражением правой относительно плоскости симметрии.
Важно заметить, что в переходной области ОВС угол a меняет свое значение от 
на границе ОВ, принадлежащей зоне максимального состояния ОАВ, где всюду 
, до 
на границе ОС, принадлежащей зоне минимального состояния О ¢ ОС, где всюду .
В решаемой задаче полностью определено предельное напряженное состояние в области ОАВ, в том числе формулой (5.22) определено приведенное среднее напряжение s. В области переходного напряженного состояния ОВС напряжения вычислены с точностью до произвольного постоянного множителя 
. Эту постоянную установим из граничного условия ОВ, приравнивая выражение (5.31) при к выражению (5.22) при 
= 0:
 .
| (5.44) |
Отсюда
, 
.
Теперь напряжения полностью определены и в области ОВС. В частности, приведенное среднее напряжение вдоль ОС согласно (5.44) и (5.31) при будет
.
Заметим, что угол раствора области переходного напряженного состояния равен 
(рис. 5.8). Используя угол раствора можно получить аналогичные выражение через формулу (5.30).
Далее приравняем к этому выражению выражение для приведенного среднего напряжения (5.20) при = 0 и 
в области O ¢ OC:
 ,
| (5.45) |
Отсюда найдем предельное давление на основание:
 .
| (5.46) |
Выражение (5.46) представляет собой формулу для предельного давления штампа (фундамента) на невесомое основание, которую иногда называют формулой Прандтля.
Проанализируем степень влияния угла внутреннего трения j на величину предельной нагрузки с помощью относительной приведенной величины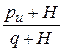 
, 
(см. табл. 5.1).
Таблица 5.1 - Влияние угла внутреннего трения j на предельную нагрузку
| j | 10° | 20° | 30° | 40° |
|
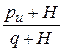
| 2,47 | 6,40 | 18,4 | 64,2 |
Приведенные данные показывают, что предельное давление на основание быстро растет с ростом прочности грунта за счет увеличения угла внутреннего трения.
Перепишем (5.46) в несколько ином виде, который нам понадобится в дальнейшем
 ,
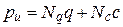| (5.47) |
где 
- коэффициенты несущей способности, зависящие от j:
 .
| (5.48) |
Используя (5.25), (5.32), а также равенство 
, можно показать, что ширина призмы выпора равна:
,
где b - ширина загруженной площади (штампа).
Предельное давление идеально-связное весомое основание. В целом данный случай вполне аналогичен случаю невесомого сыпучего основания (рис. 5.9). Зоны OAB и O ¢ OC соответствуют максимальному и минимальному напряженному состоянию, зона OBC суть область радиального веера. При этом в зоне OAB , в зоне O ¢ OC , а в области радиального веера OBC 
.
Рисунок 5.9. - К определению несущей способности идеально-связного основания
В зоне максимального напряженного состояния OAB согласно (5.36), (5.40) и рис. 5.11 имеют место равенства
 .
| (5.49) |
Сетка линий скольжения имеет очертание равнобедренного треугольника с прямым углом при вершине и шириной призмы выпора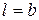 
. Это обусловлено тем, что линии скольжения 1-го семейства переходной области представлены окружностями, как было показано в п. 5.2.4.
Для переходной зоны O ¢ OC согласно (5.40), (5.43) и (5.49) можно записать
,
 .
| (5.50) |
Из (5.50) видно, что в отличие от невесомой среды здесь в переходной зоне напряжения зависят от глубины. Тогда на границе OC, учитывая, что , выражение для напряжений примет вид
 ,
| (5.51) |
Сравнивая (5.51) и формулу (5.37) для напряжений в зоне минимального напряженного состояния O ¢ OC имеем
 ,
|
Полагая здесь p равное искомому pu, запишем уравнение для предельного давления на идеально-связное основание
 ,
| (5.52) |
Полученное уравнение иногда называют формулой Прандтля для предельного давления на идеально-связное основание.
|
|
|
