Выражение (2.27) можно записать в виде 13 глава

где j _i, c_i - угол внутреннего трения и удельное сцепление грунта, в котором находится подошва i -го отсека, l_i - длина подошвы i -го отсека.

Теперь, с помощью (5.74)…(5.76) найдем искомые силы, действующие на поверхности скольжения, по всем отсекам.

Для ответа на главный вопрос об обрушении склона используют коэффициент устойчивости, определяемый в нашем случае как

, (5.77)

где 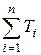- сумма сил трения по поверхности скольжения, удерживающих склон; - сумма сдвигающих сил, действующих также по поверхности скольжения; n - количество отсеков.

Выражение (5.77) можно записать в развернутом виде с учетом (5.75), (5.76):

.

В случае, когда на поверхности склона заданы внешние нагрузки, поступают следующим образом. В пределах соответствующих отсеков определяют равнодействующие внешних воздействий P_i, которые, как и собственный вес, прикладывают к середине подошвы отсека. Тогда выражения (5.75) для нормальной и касательной силы в уровне подошвы примут вид

, ,

а коэффициент устойчивости можно переписать так:

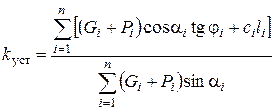. (5.78)

Если коэффициент устойчивости больше единицы, это означает, что величина удерживающих сил больше, чем сдвигающих, и, следовательно, склон устойчив. Однако сказанное справедливо только для одной рассчитанной линии скольжения.

Очевидно, что если принять линию скольжения другой формы или просто расположенную иначе, то система сил и, соответственно, коэффициент устойчивости изменятся. Таким образом, приходим к необходимости поиска опасной линии скольжения, которой бы отвечал минимальный коэффициент устойчивости. Именно он и является действительным коэффициентом запаса устойчивости по этому методу расчета, а соответствующая ему линия скольжения будет опасной. Эта задача формулируется как задача поиска минимального коэффициента устойчивости и решается методами вариационного исчисления:

, (5.79)

где z (x) - неизвестная функция, определяющая форму и положение поверхности скольжения.

Если задаться какой-либо определенной формой линии скольжения, то задача существенно упрощается.

Далее рассмотрим наиболее распространенную модификацию метода отсеков - метод круглоцилиндрических поверхностей скольжения.

В этом методе предполагается, как видно из названия, что поверхность скольжения, по которой может произойти сдвиг грунта, представляет собой некоторую круглоцилиндрическую поверхность. Изложение метода проиллюстрируем применением его к расчету устойчивости откоса, в частности, откоса земляного полотна железной дороги. Он также широко используется для расчета устойчивости оснований сооружений. К этому случаю нетрудно перейти, развернув откос в основание.

Допустим, что в момент обрушения откоса область обрушения ABC (рис. 5.20, а) поворачивается вокруг мгновенного центра вращения О как жесткое тело с некоторой скоростью w. В механике сплошной среды одним из фундаментальных является принцип виртуальных мощностей, согласно которому мощность работы внешних сил на виртуальных скоростях должна быть равна мощности работы внутренних сил на тех же скоростях. В рассматриваемой задаче к внешним силам относятся давление от подвижного состава, веса верхнего строения пути на земляное полотно и собственный вес области обрушения ABC. К внутренним силам относятся нормальные и касательные силы, действующие на поверхности скольжения AB.

 

Рисунок 5.20. - К расчету методом круглоцилиндрических поверхностей скольжения

 

Мощность работы внешних сил выражается произведением 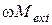, а мощность работы внутренних сил - произведением 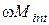, где , - суммарные моменты внешних и внутренних сил относительно точки O. Поскольку внутренние силы определяются на поверхности скольжения, то они, следовательно, имеют предельные значения. Чтобы воспользоваться принципом виртуальных мощностей, внешние силы также должны быть предельными. Для этого их необходимо увеличить в такое число раз, чтобы было справедливым равенство виртуальных мощностей работы внешних и внутренних сил:

или

Величина

,

(5.80)

таким образом, представляет собой коэффициент устойчивости.

Момент внешних сил находится просто. С этой целью разделим область обрушения на n вертикальных отсеков шириной b_i. Подсчитаем их вес 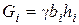, где h_i - средняя высота i -го отсека, а также результирующие там, где имеется давление р. После этого можем записать

где l_i - плечи сил P_i и G_i.

Поскольку нормальные к поверхности скольжения силы проходят через центр вращения О, то момент внутренних сил определяется одними внутренними силами трения T_i:

Предельная величина этих сил выражается законом Кулона аналогично (5.76):

где 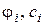- угол внутреннего трения и удельное сцепление грунта в пределах подошвы 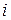-го отсека; - длина подошвы отсека.

Для установления силы 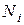рассматривают равновесие i -го отсека (см. рис. 5.20, б) в предположении, как и ранее, что силы 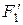и , действующие на боковые грани отсека, самоуравновешены. Тогда величину силы 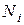определим, спроектировав все силы на направление нормали к подошве отсека (на направление радиуса, проходящего через центр подошвы отсека):

Собирая результаты, получим вполне аналогично (5.78)

.

(5.81)

Суммирование здесь выполняется по всем отсекам.

По формуле (5.81) можно вычислить коэффициент запаса устойчивости для любой выбранной круглоцилиндрической поверхности скольжения. Задача дальше заключается в том, чтобы отыскать наиболее опасную (экстремальную) поверхность скольжения, для которой коэффициент запаса устойчивости принимает минимальное значение. Иначе говоря, следует отыскать минимум функции (5.81). Как нетрудно видеть, коэффициент запаса устойчивости является функцией трех переменных: двух координат центра вращения и радиуса 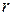, в отличие от (5.79), где коэффициент устойчивости зависел от неизвестной функции.

В математике разработаны достаточно эффективные методы поиска экстремумов функции многих переменных. Тем не менее, задача эта достаточно трудоемкая. Если, однако, принять допущение, что экстремальная поверхность скольжения обязательно проходит через точку A, то коэффициент запаса устойчивости становится функцией координат центра вращения и трудоемкость решения задачи существенно уменьшается.

В целях упорядочения поиска экстремальной поверхности скольжения и соответствующего центра вращения рекомендуется следующая методика. Через точку А в направлении возможного положения экстремального центра вращения проводится прямая АА ₁ (рис. 5.21). На этой прямой выбирается несколько центров вращения О ₁, О ₂, … с радиусами 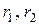,... через точку А проводятся поверхности скольжения I, II,.... Дня них рассчитываются коэффициенты запаса устойчивости 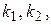…. Перпендикулярно прямой АА₁ в некотором масштабе откладываются значения 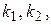…. Полученные точки соединяют гладкой кривой. К ней проводится касательная, параллельная прямой АА ₁. Координаты точки касания 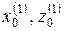в первом приближении определяют координаты экстремального центра вращения, а соответствующее значение - в первом приближении экстремальный коэффициент устойчивости.

Рисунок 5.21. - Поиск экстремума в методе круглоцилиндрических

поверхностей скольжения

Для того, чтобы получить второе приближение, через точку относительного минимума проводится прямая DD ₁ ортогонально прямой АА ₁. На прямой DD ₁ выбирается ряд мгновенных центров вращения О ¢₁, О ¢₂, …, и процесс повторяется. Итерации могут быть продолжены до тех пор, пока коэффициент запаса устойчивости не будет определен с достаточной степенью точности. Описанный процесс может быть запрограммирован для решения задачи с помощью ЭВМ.

Обратим внимание на то, что в изложенной методике оценки устойчивости все внешние силы, в том числе такие, как собственный вес грунта, увеличиваются в одинаковой мере в k раз. Вряд ли такой подход можно считать наилучшим. Существует и другая возможность - принять, что обрушение откоса происходит вследствие роста давления p. Используя равенство , будем иметь

,

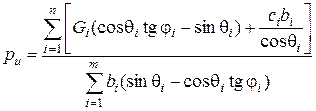(5.82)

где m - число отсеков в пределах полосы давления.

Из этой формулы видно, что возможные положения мгновенного центра вращения ограничены условием

Задача сводится к определению экстремальной поверхности скольжения с наименьшим значением p_u.

При поиске нужно иметь в виду существование так называемых локальных минимумов, отвечающих линиям скольжения, по которым может произойти сползание незначительной части склона, практически не влияя на остальной массив. Далее, считается, что если минимальный из всех найденных коэффициентов устойчивости больше единицы, то склон находится в равновесии, если меньше единицы, то произойдет обрушение. Здесь следует помнить, что точность получаемых результатов в данном методе зависит от того, насколько качественно решены два вопроса - вопрос об очертании линии скольжения (для линий заранее заданной формы) и вопрос о силовом взаимодействии между отсеками.

 

5.4 Предельное давление грунта на ограждения

 

5.4.1. Активное давление грунта

 

Активным называют предельное давление грунта на стенку, образующееся при отодвигании стенки от грунта и обрушении грунта в сторону стенки. Другое определение: активное давление - это максимальное давление грунта на стенку, при котором произойдет обрушение грунта в сторону стенки. Экспериментально полученный график давления грунта в некоторой точке задней грани стенки в процессе ее отодвигания показан на рис. 5.22. Видно, что при перемещении стенки на величину давление грунта падает до минимального значения и далее остается постоянным. Это давление и является активным. Эксперименты показывают, что для образования активного давления достаточно весьма незначительного смещения стенки, измеряемого обычно долями миллиметра. Такое смещение практически всегда имеет место вследствие деформаций грунта в основании стенки и перед ней, а также самой стенки. Поэтому активное давление можно считать постоянно действующим давлением грунта на стенку.

 

 

Рисунок 5.22. - Зависимость давления от перемещения стенки

 

 

Определим величину активного давления (рис. 5.23). Для общности предположим, что сверху действует нагрузка p. На глубине z главные напряжения равны:

 

Рисунок 5.23. - К определению активного давления

 

,

Подставим эти значения в закон Кулона-Мора, имеем

;

;

.

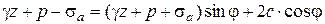Тогда выражение для активного давления примет вид:

. (5.83)

Отметим еще, что с помощью равенств

формулу (5.83) можно преобразовать к виду, в котором она часто употребляется:

,

где величину

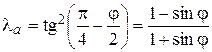(5.84)

называют коэффициентом активного давления грунта.

Согласно этой формуле эпюра активного давления линейна (рис. 5.24). При отсутствии или малой величине внешнего давления р и при наличии сцепления в грунте () в верхней части эпюры на глубину

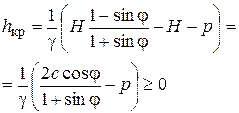
Рисунок 5.24. - Эпюры активного давления

 

образуется участок отрицательного давления грунта на стенку (см. рис. 5.24). Принято, однако, считать, что удельная сила прилипания грунта к стенке мала и поэтому участок эпюры с растягивающим напряжением реализовываться не может. На участке принимают = 0, в результате чего оказывается, что этот слой грунта не приходит в предельное состояние. В сыпучем грунте (с = Н = 0) эта проблема не возникает — эпюра активного давления всюду положительна (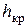 = 0), имея треугольную форму.

Результирующая активного давления на один метр длины стенки в случае, когда эпюра имеет вид треугольника 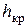> 0, определяется площадью треугольника давления:

где 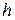— высота стенки; — активное давление на уровне подошвы стенки (.

Линия действия ее проходит через центр тяжести треугольника давления, т.е. на расстоянии от уровня подошвы стенки.

В случае трапецеидальной формы эпюры давления (рис. 5.24) ее результирующую удобно представить в виде суммы составляющих и 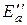соответственно от прямоугольной и треугольной частей эпюры:

,

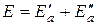где ; ; 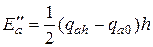— активное давление на уровне поверхности грунта ( = 0).

Составляющие и 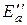действуют на расстояни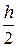и и 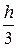от уровня подошвы.

Покажем, что полученное выражение для активного давления является полностью корректным с точки зрения строгой постановки ТПРГ.

Призма обрушения (рис. 5.25) состоит из областей максимального напряженного состояния ОАВ, переходного состояния ОСВ и минимального напряженного состояния ОСО. Для упрощения решения задачи положим, что задняя грань стенки ОА вертикальная и абсолютно гладкая (силами трения грунта о стенку пренебрегаем). Нормально к поверхности грунта ОО приложено внешнее давление . Так как на ОО давление известно, то напряженное состояние в области ОСО полностью определено формулами (5.20). В том числе на границе ОС согласно (5.21) при = 0 имеем

.

(5.85)

Граница ОС составляет с осью угол . Положим в (5.) и приравняем его к (5.85):

Рисунок 5.25. - Сетка линий скольжения для активного давления

 

 

.

Отсюда произвольная постоянная

Теперь полностью определено напряженное состояние и в области ОВС. Граница ОВ этой области составляет с осью угол . На этой границе согласно (5.) и (5.)

Приравняв это выражение к правой части (5.) при = 0

определим предельное давление грунта на стенку

которое и является активным давлением.

Важное практическое значение имеет частный случай, когда поверхность грунта за подпорной стенкой горизонтальна.

При горизонтальной поверхности грунта угол = 0 и области ОАВ и ОСО смыкаются в одну общую область минимального напряженного состояния (рис. 5.24), а область переходного состояния вырождается. Сетка линий скольжения представлена отрезками прямых, наклоненных к оси Oz под углами ± . Компоненты напряжений определяются формулами (5.), причем напряжение есть не что иное, как активное давление грунта на стенку, в котором учтено влияние собственного веса грунта:

 

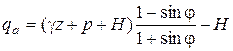
5.4.2. Пассивное давление грунта

 

Пассивным называют предельное давление грунта на стенку, образующееся при надвигании стенки на грунт. Другое определение: пассивное давление - это минимальное давление грунта на стенку, при котором произойдет выпор грунта от стенки. График изменения давления грунта в некоторой точке грани стенки в процессе надвигания показан на рис. 5.26. Видно, что при перемещении стенки на величину давление грунта возрастает до максимального значения и далее остается постоянным. Это давление и является пассивным. Эксперименты показывают, что для образования пассивного давления необходимо достаточно большое перемещение стенки, измеряемое миллиметрами или даже сантиметрами. Такое смещение не всегда возможно или допустимо. Поэтому в отличие от активного пассивное давление не всегда следует принимать в расчетах в полную величину.

 

 

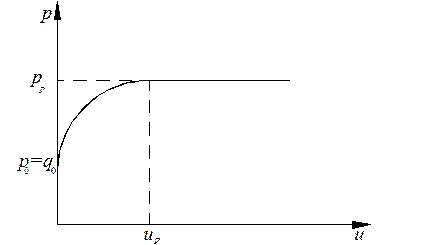
Рисунок 5.26. - График изменения давления грунта в некоторой точке грани стенки

в процессе надвигания

 

Определим пассивное давление. Как и ранее, эту грань, пренебрегая силами трения, будем считать абсолютно гладкой. Расчетная схема показана на рис. 5.27. На поверхности действует пригрузка q. Главные напряжения определятся как

,

Подставим эти значения в закон Кулона-Мора, имеем

;

.

 

 

Рисунок 5.27. - К определению пассивного давления

 

Окончательно выражение для активного давления примет вид:

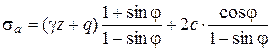. (5.85)

Отметим еще, что с помощью равенств

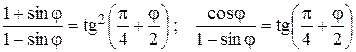
формулу (5.85) можно преобразовать к виду, в котором она часто употребляется:

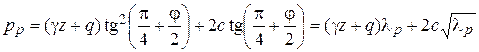
где

(5.86)

есть коэффициент пассивного давления грунта.

Покажем, что полученное решение является строгим решением ТПРГ. На поверхности действует равномерное приведенное давление . В таком случае перед стенкой образуется область максимального напряженного состояния грунта ОАВ (рис. 5.28), которую также называют призмой выпора, поскольку грунт, находящийся в ней, выдавливается надвигающейся стенкой. Сетка линий скольжения состоит из отрезков прямых, наклоненных к оси Ox под углами ± , а напряженное состояние с учетом собственного веса грунта определяется формулами (5.). Пассивное давление можно найти по формуле для :

В случае непригруженного (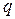 =0) сыпучего грунта (с = Н = 0) эпюра пассивного давления имеет треугольную форму, а в остальных случаях трапецеидальную. В первом случае результирующая сила пассивного давления на один метр стенки

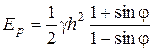
действует на расстоянии 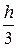от уровня ее подошвы.

 

Рисунок 5.28. - Эпюры и сетка линий скольжения для активного давления

 

Во втором случае результирующую удобно представить в виде суммы составляющих 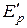и соответственно от прямоугольной и треугольной частей эпюры давления:

, ;

где — пассивное давление на уровне поверхности грунта (z = 0); — пассивное давление на уровне подошвы стенки ().

Составляющие 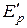и действуют на расстояниях 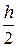и 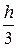от подошвы стенки соответственно.

 

5.4.3. Определение активного и пассивного давления грунта методом плоских поверхностей скольжения (метод Кульмана)

 

Активное давление грунта определяется в следующем порядке.

При решении этой задачи графоаналитическим методом назначают ряд возможных положений плоской поверхности скольжения, определяемых значением угла b (рис. 5.29). Если поверхность грунта свободна от давления, то на выделенную призму обрушения действует сила , сила веса призмы , реакция грунта и стенки 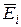(рис. 5.30).

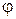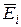Сила согласно закону Кулона отклонена от нормали к поверхности скольжения на угол так, что препятствует сдвигу. С учетом трения грунта о стенку реакция принимается отклоненной от нормали к задней грани стенки на угол . Неизвестные силы и определяются путем построения замкнутого многоугольника сил (рис. 5.30). По результатам вычислений можно построить график зависимости от угла (рис. рис. 5.31). Приведенная величина активного давления соответствует максимуму графика. Действительная нормальная и касательная составляющие будут:

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: