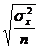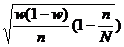Формулы средней ошибки выборки

Некоторые основные термины статистики

 

Статистика - раздел математики о методах анализа данных с целью построения вероятностных моделей массовых случайных явлений^. Методы статистики используются во всех областях и всех видах научных исследований, где приходится иметь дело с большими объемами числовых данных, характеризующих процесс (природный, техногенный, социально-экономический).

 

Уровни стат.обработки данных:

А) Описательная статистика – методы визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.),. Некоторые методы описательной статистики - кластерный анализ, многомерное шкалирование.

Б) Теория оценивания,

В) теория проверки гипотез - используют математическое ожидание, медиана, стандартное отклонение, квантили, плотности и функции распределения для изучения и прогнозирования разных процессов.

 

Выборка, виды выборки.

Генеральная совокупность – это тот массив данных, о которых вы хотите сделать выводы. Выборка - часть ГС, по которой делают статистические выводы о ГС, выборка должна быть репрезентативной.

· Генеральная совокупность – полное множество объектов. ( Изучать генеральную совокупность объектов сложно или невозможно физически, поэтому стат.анализу подвергают часть генеральной совокупности – в ыборку ).

· Выборка – часть объектов из генеральной совокупности, отобранных для изучения. Стат. показатели, рассчитанные по выборке, могут с некоторой погрешностью служить оценками аналогичных показателей ген. совокупности. Допустимая погрешность может быть задана заранее, до сбора данных – s (w) выражается в долях или процентах (например 30%-ная погрешность – т.е. ошибка s=0,3). Чем меньше объем выборки, тем сильнее погрешность.

Обозначения, используемые для отличия показателей ген. совокупности от выборки.

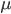- математическое ожидание генеральной совокупности – наиболее вероятное, характерное, частое  значение, к которому стремится бОльшая часть генеральной совокупности. В выборке матожиданию соответствует приближенная его оценка – среднее (среднее арифметическое, среднее, геометрическое, среднее квадратическое и т.п. расчетные средние)

Долей выборки k_n называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: k_n = n/N.

Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n: w = n_n/n.

 

В генеральной совокупности средняя (матожидание) обозначается µ (мю), в выборочной x̅ (х с чертой) это средние арифметические по каждому виду совокупности.

Между показателем генеральной совокупности и выборки есть некоторое различие, зависящее от конкретного множества элементов выборки, так что разница между выборочным и генеральным значением показателя дает статистическую погрешность (она называется абсолютной - или предельной - ошибкой Δ) оценки стат.показателя. Δ = t·μ, где t – коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t) по таблице интегральной функции Лапласа. Соотношение между пределом ошибки выборки (_Δ), гарантируемым с некоторой вероятностью Р(t), и средней ошибкой выборки имеет вид: или

 

Также в расчетах часто используется относительная погрешность m_r (ошибка) оценки стат.показателя. Она = Δ/t_кр, где t_кр - критическое значение распределения Стьюдента, например, взятое из справочных таблиц или рассчитанное в программе стат.анализа (например, в Excel есть функция СТЬЮДРАСПОБР()).

 

Формулы средней ошибки выборки