 |
Способы организации выборки из ГС
|
|
|
|
Выборки м.б. (1) вероятностными (случайными) или (2) неслучайными:
1. Случайная выборка - при отборе элементов из генеральной совокупности используется таблица случайных чисел, либо:
- механическая (систематическая) выборка - 1-элемент отбирается случайно, затем, с шагом n, отбирается k элементов из генеральной совокупности (объемом N=n*k элементов)
- стратифицированная (районированная) генеральная совокупность условно разбивается на группы, из каждой группы отбираются случайным или механическим способом элементы в выборку;
- серийная (гнездовая или кластерная) выборка – генеральная совокупность условно разбивается на группы, затем в выборку целиком берутся группы, отобранные среди остальных случайным образом;
2. Невероятностные (не случайные) выборки. Отбор элементов ген.совокупности делается не случайным образом, а по принципу удобства, типичности, равного представительства и т.д. Например,
- Квотная выборка - выделяется ряд групп, в каждой обследуется количество объектов пропорциональное доле группы в генеральной совокупности, - либо от каждой группы поровну, случайно.
- Выборка методом снежного кома – у респондентов, начиная с первого, берутся контакты его друзей, коллег, знакомых, которые подходят под условия исследовании. Такой прием используют, когда надо опросить людей одного круга, достатка, профессии).
- Стихийная выборка - опрашиваются доступные респонденты (интернет-опросы).
- Выборка типичных случаев – отбор объектов со средним (типичным) значением признака.
Также выборки могут повторными (из генсовокупности один и тот же элемент может попасть в выборку несколько раз) и бесповторными (после отбора элементов в выборку, элемент исключается из дальнейшего использования в выборках)).
|
|
|
Размер выборки
Выборка должна быть репрезентативной, т.е. достоверно отражать всю генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей. Пример: - Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население Москвы. А Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России. Есть спец. приемы в статистике, чтобы выборка считалась репрезентативной - например, размер выборки рекомендуется брать не произвольным, а с учетом объема всей ген.совокупности.
Одномерная выборка считается малой, если ее объем выборки не превышает 30 (n <= 30). Для многомерных выборок размерности k, при измерении k признаков, малая выборка – это когда n/k < 10).
Выводы стат.анализа выборки с определенной погрешностью отражают свойства ген.совокупности. Например, о населении региона судят по нескольким сотням или тысячам опрошенным. От характеристик тех, кто попал в выборку, зависит результат общения стат. выводов обо всем населении региона – с определенной погрешностью.
До сбора данных, с учетом заранее заданной погрешности дальнейших расчетов надо правильно выбрать объем выборки n – его выясняют в зависимости от типа выборки, размера генеральной совокупности N, уровня достоверности (доверительной вероятности) полученного результата и целей (что именно собираются делать с выборкой[1]).
При проведении исследований, которые определяют распространенность некоей характеристики в генеральной совокупности. Рассчет размера выборки необходим для того, чтобы полученные оценки имели желаемую степень достоверности. Обычно желательна 95%-ная степень достоверности. Это значит, что предельно допустимая вероятность ошибки в расчетах =5 %, а с 95%-ной вероятностью в доверительном интервале лежит реальное значение статического параметра генеральной совокупности, оцененного по результата стат.анализа выборки из генеральной совокупности.
|
|
|
Рекомендуемый объем выборки из ген.совокупности зависит от
- типа выборки (повторная/бесповторная),
- показателя ген.совокупности, который оценивается по выборке из ГК матожидание или дисперсия или доля элементов с определенным значением и т.п.),
- способы отбора данных Г.С. в выборку (гнездовая, сплошная и т.д.)
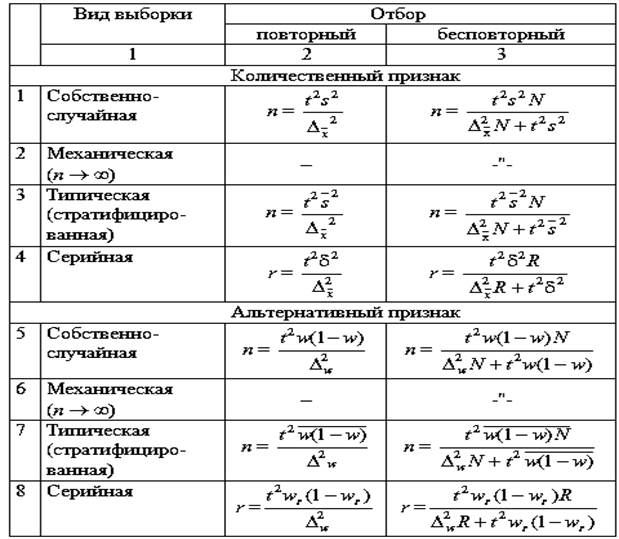
Здесь[2]:
N- размер генеральной совокупности (Г.С.), n – рекомендуемый размер выборки из Г.С.,
S (или SD, standard deviation) - стандартное отклонение выборки (для генеральной совокупности это среднеквадратичное отклонение σ (сигма)),
∆ - предельная ошибка оценки матожидания (среднего арифметического) или доли. Формула предельной ошибки: ∆ = t*mr где mr (standard error или стандартная ошибка средней) – т.н. ошибка репрезентативности. t – значение распределения Стьюдента в зависимости от допустимой (доверительной) вероятности, для простоты
· для доверительного интервала 95 % используется t=2,
· для доверительного интервала 99 % используется t=3
· и для доверительного интервала 68 % используется t=1.
Выборку в стат.анализе представляет числовой ряд. Бывают выборки 1-мерные и многомерные.
1) Ряды атрибутивные (содержат качественные значения)или вариационный (числовые значения),
2) Ряды динамики (временными рядами) отображают процесс во времени. Ряды динамики бывают:
ü моментные (уровни рядов динамики могут относиться к определенным датам (моментам) времени) и
ü интервальные (каждый элемент такого ряда - усредненные за период данные).
3) Панельные данные (1+2) - набор данных среза – но в динамике во времени) – это область многомерного стат.анализа.
Цензурированной выборкой называется выборка, элементами которой являются полные наработки[3] и неполные наработки (наработки до цензурирования)[4] или только значения наработки до цензурирования. Такие выборки характерны для показателей надежности объектов, достоверности обработки информации, защиты информации.
Смыкание рядов динамики.
|
|
|
При изучении явлений встречаются случаи, когда показатели, характеризующие данное явление, имеются в справочниках до какого-либо периода, а далее они или вообще не приводятся, или даются несопоставимыми с предшествующими данными (т.е. смыкаемые ряды неоднородны по кругу охватываемых объектов, по единице измерения).
Например, в справочнике о внешней торговле опубликованы индексы (%) физического объема экспорта страны N:
| 1995 | 1996 | 1997 |
| 100 | 139 | 153 |
В другом справочнике тоже опубликованы данные о физическом объеме экспорта этой же страны N:
| 1997 | 1998 | 1999 | 2000 |
| 100 | 120 | 156 | 176 |
Надо соединить их в 1 выборку – но сделать это простым соединением не получится, т.к. данные рядов несопоставимы: показатели первого ряда рассчитаны на базе 1995 г. и составляют 100%, а показатели второго ряда на базе 1997 г. и соответствуют тоже 100%.
Чтобы показатели этих рядов стали сопоставимы, надо произвести смыкание рядов.
А) Для пересчета показателей второго ряда на базе 1995 года - определить коэффициент пересчета, который получают путем деления общего показателя первого ряда на общий показатель второго ряда, т.е. 153/100 = 1,53. Затем показатели второго ряда за 1998, 1999, 2000 годы умножают на этот коэффициент: 120 * 1,53 = 184; 156 *1,53 = 239; 176 * 1,53 = 269. Полученными таким путем показателями заполняем объединенный ряд (1995 г. = 100).
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 100 | 139 | 153 | 184 | 239 | 269 |
Б) Либо можно было взять в качестве базы элементы не первого ряда, в второго. Для пересчета показателей первого ряда на базе 1997 г. определяем коэффициент пересчета путем деления показателя 2-го ряда на показатель 1-го ряда: 100/153 = 0,6535. Затем показатели 1-го ряда за 1995 и 1996 г. умножаем на этот коэффициент, т.е. 100 * 0,6535 = 65,4; 139 * 0,6535 = 90,8. Полученными таким образом показателями заполняем объединенный ряд (1997=100).
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 65 | 91 | 100 | 120 | 156 | 176 |
О доверительном интервале
Когда стат.показатели ген.совокупности считают (точнее, приближенно оценивают) по выборке, оценка содержит стат.погрешность. Окончательный вывод о значении стиат.показателя ген. совокупности должен выдаваться не как 1 число, а как интервальная оценка т.е. доверительный интервал, в который попадает неизвестное значение показателя ген.совокупности: PГ.С.? [Рвыб-ошибка; Рвыб+ошибка ]
|
|
|
Доверительный интервал – вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности. Доверительный интервал является т.н. интервальной оценкой какого-либо стат.показателя Г.С., т.е. таким диапазоном значений вокруг выборочного показателя, в который с заранее заданной доверительной вероятностью (обычно 95%-ной из 100%, т.е. 0,95) попадает значение оцениваемого параметра генеральной совокупности. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины ГС. Чем шире интервал, тем больше стат.ошибка оценки стат.показателя Г.С..
Существуют разные методы определения доверительного интервала, например:
· через медиану и среднеквадратическое отклонение;
· через критическое значение t-статистики (коэффициент Стьюдента).
Этапы разных способов расчета доверительного интервала для некоторого стат.показателя генеральной совокупности:
1. формируем выборку из генеральной совокупности (предварительно выяснив размер выборки);
2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;
3. рассчитываем доверительный интервал двумя способами;
4. анализируем очищенные выборки и полученные доверительные интервалы.
Этап 1. Выборка данных
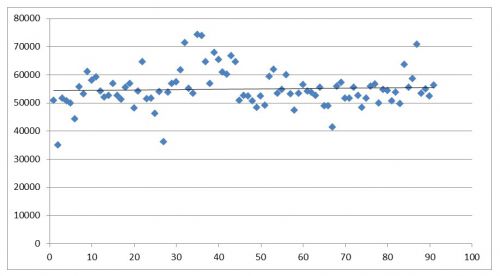
|
|
|


