 |
Статистическая оценка и ее погрешность.
|
|
|
|
Статистика оперирует большими выборками данных, характеризующих некий процесс. От того, какие случайные данные оказались в выборке, зависит статистический вывод, так что для разных выборок значений факторов одного и того же процесса или объекта результат будет немного отличаться. Параметры процесса вычисляются как приближенная оценка на основе выборки - с некоторой погрешностью по сравнению с неким неизвестным, но предполагаемым значением показателя.
Оценки бывают
· точечными (в них погрешность еще не учтена) (сначала их рассчитывают для выборки),
· интервальными (в них указан разброс, диапазон отклонения оценки от истинного значения с учетом ошибки). Размеры разброса называются доверительным интервалом [12].
Например, оценкой математического ожидания некоего показателя, описанного выборкой, служат среднее арифместическое, среднее геометрическое, медианное среднее и т.д., которые рассчитываются с заранее известно погрешностью, т.е. точное значение матожидания конкретного фактора лежит где-то в пределах доверительного интервала: оценка матожидания (ср.арифметическое) плюс-минус абсолютная статическая погрешность.
Разница между статистической оценкой и неизвестным значением оцениваемого показателя называется статистической погрешностью. Считается, что с ростом размера выборки, выборочные показатели оцениваются все точнее, а погрешность оценки уменьшается.
Виды ошибок и погрешностей:
Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Относительная погрешность – это число, отражающее степень точности измерения.
|
|
|
Систематические ошибки - когда нарушают правила отбора объектов в выборку.
Статистическая ошибка ( ошибка выборки). Погрешности оценки стат.показателя или прогноза различны в зависимости от нескольких причин:
- от размера выборки (много данных или мало[13] - Ошибки репрезентативности [14] - выборочная совокупность не полностью воспроизводит генеральную),
- от типа данных (значения ли это показателя или лишь частоты значений),
- от характера распределения значений в выборке (нормальное распределение, присущее случайным числам, или нет).
Ошибка выборочного наблюдения - разность между значением параметра в генеральной совокупности и ее выборочным значением. Ошибки выборки разные для разных способов выборок. Ошибка выборки бывает средняя и предельная.
А) Средняя ошибка m выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной (чем больше наблюдений и чем меньше разброс признака в ряду данных, тем меньше средняя ошибка выборки m). Конкретные формулы расчета средней ошибки (погрешности) оценки некоторых стат.показателей см. в таблице ниже:
(Далее в таблице обозначения: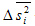 
- средняя из внутригрупповых выборочных дисперсий для непрерывного признака;
- средняя из внутригрупповых дисперсий доли; r — число отобранных серий, R — общее число серий;
, где 
— средняя i-й серии; а второе слагаемое — общая средняя по всей выборочной совокупности для непрерывного признака;
, где 
— доля признака в 
-й серии; 
— общая доля признака по всей выборочной совокупности.)
Б) Предельная (максимальная) ошибка выборки Δ вычисляется по формуле 
, где коэффициент t (критерий Стьюдента, "коэффициент доверия"), предложенный У.С. Госсетом (псевдоним "Student"); хранятся в таблице распределений Стьюдента (см. приложение) и выбираются с учетом заранее заданной исследователем доверительной вероятности Ф(t) правильности вывода о репрезентативности выборки.[15]
|
|
|
Предельная ошибка выборки Δ позволяет определить предельные значения характеристик генеральной совокупности.
В табл. - формулы для вычисления предельной ошибки разных способов выборки.
|
|
|
