для средней и доли (р) для разных видов выборочного наблюдения

Относительн ая ошибки выборки для статистических показателей выборки

Интервальная оценка стат. показателя - диапазон, в который с заранее заданной доверительной вероятностью (близкой к 1) попадает рассчитанный параметр. Д оверительные интервалы:

Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя — путем ее добавления.

Доверительный интервал для средней

-  с заданной вероятностью Р, которая называется доверительным уровнем и определяется значением t, можно утверждать, что истинное значение средней лежит в пределах от ,а истинное значение доли w — в пределах от

При расчете доверительного интервала для трех стандартных доверительных уровней Р = 95%, Р = 99% и Р = 99,9% значение t выбирается по таблице Стьюдента. Приложения в зависимости от числа степеней свободы v=n-1. Если объем выборки достаточно велик, то соответствующие этим вероятностям значения t равны: 1,96, 2,58 и 3,29.

 

Формулы определения доверительных границ:

• для средних величин (М): М_ген = М_выб ± tm
• для относительных показателей (Р): Р_ген =Р_выб ±tm, где М_ген и Р_ген - соответственно, значения средней величины и относительного показателя генеральной совокупности; М_вы6 и Р_вы6 - значения средней величины и относительного показателя выборочной совокупности; m - ошибка репрезентативности;
  t - критерий достоверности (доверительный коэффициент).

 

Способы распространения выборочных данных на генеральную совокупность.

Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов.

 

1) П рямой пересчет – умножить выборочное среднее на объем генеральной совокупности N. Например, если выяснили на основе выборки среднее число детей ясельного возраста в городе = человека, то для оценки потребности в яслях умножают это среднее на объем генеральной совокупности N = 1000, т.е. составит 1200 мест.

2) Способ коэффициентов нужен когда выборку изучают с целью уточнить данные сплошного наблюдения.

При этом используют формулу:

,

где все y — это численность совокупности:

§ — с поправкой на недоучет,

§ Y1, Y0 - без этой поправки,

§ Y0 — в контрольных точках

§ Y1 — в тех же точках по данным контрольных мероприятий.

 

Пример. Оценка вероятности (генеральной доли) р.

При механическом выборочном способе обследования социального положения 1000 семей выявлено, что доля малообеспеченных семей составила w = 0,3 (30%) (выборка была 2%, т.е. n/N = 0,02). Необходимо с уровнем достоверности р = 0,997 определить показатель р малообеспеченных семей во всем регионе.

Решение. По представленным значениям функции Ф(t) найдем для заданного уровня достоверности Р = 0,997 значение t = 3 (см. формулу 3). Предельную ошибку доли w определим по формуле из табл. 9.3 для бесповторного отбора (механическая выборка всегда является бесповторной):

Предельная относительная ошибка выборки в % составит:

Вероятность (генеральная доля) малообеспеченных семей в регионе составит р=w±Δ_w, а доверительные пределы р вычисляются исходя из двойного неравенства:

w — Δ_w ≤ p ≤ w — Δ_w, т.е. истинное значение р лежит в пределах:

0,3 — 0,014 < p <0,3 + 0,014, а именно от 28,6% до 31,4%.

Таким образом, с вероятностью 0,997 можно утверждать, что доля малообеспеченных семей среди всех семей региона составляет от 28,6% до 31,4%.

Приложение 1.

Для сравнения количественного показателя в двух равновеликих независимых группах объем каждой выборки рассчитывается по формуле:

,

где и – дисперсии признака в обеих группах; Δ – минимальная (клинически значимая) величина различий, которую необходимо обнаружить; Za и Zb – критические значения нормального стандартного распределения для заданных α и β (односторонний или двусторонний тест, в зависимости от формулировки альтернативной гипотезы), определяются по табл. 1 [1].

Таблица 1

Критические значения Z стандартного нормального распределения

Уровень знач.	0,005	0,01	0,012	0,02	0,025	0,05	0,1	0,15	0,2	0,25	0,3
Одностор. тест	2,567	2,326	2,257	2,054	1,96	1,645	1,282	1,036	0,842	0,674	0,524
Двусторон. тест	2,807	2,576	2,513	2,326	2,242	1,960	1,645	1,440	1,282	1,150	1,036

Иногда по финансовым, этическим или другим причинам исследователь ограничен в своих возможностях набрать группу достаточной численности (как правило, это касается опытной группы). Если известна фиксированная численность одной выборки n1, то численность другой определяется следующим образом:

.

Если сравниваются доли p1 и p2, частота встречаемости номинального признака, то объем выборки:

.

здесь Δ – минимальная клинически значимая разница между долями; p1 и p2 определяется основываясь на подобных исследованиях из литературных источников, или на основе пилотного проекта. Как крайний случай можно выбрать p1=0,5 и p2=0,5, при этом численность выборки будет неоправданно завышена.

Если доля определена в %, то в выражении вместо 1 берется 100.

Такой метод дает достаточно точные результаты при 0,25<p<0,75. В других случаях вводится поправка

.

При этом объем выборки:

.

Если объем одной выборки фиксирован, то объем второй

.

Расчет объема выборки при эпидемиологических исследованиях

Вид выборки. Простая случайная выборка (простой рандомизированный отбор). При этом любая единица выборки имеет равные шансы быть отобранной с помощью жеребьевки, таблиц или компьютерного генератора случайных чисел.

Известна численность генеральной совокупности. Обычно эти данные можно получить из результатов переписи населения, отчетности статорганов, в которых указывается возрастной, половой, социальный и т.д. состав определенного региона (района, города, страны).

Для количественных признаков

.

где N – объем генеральной совокупности; Δ – ошибка выборки – это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности, также как и уровень значимости ошибка выборки задается самим исследователем. Ее предварительная оценка (предпочитаемая величина перед подстановкой в формулу) часто произвольна. Как правило, не рекомендуется принимать ошибку выборки выше 5 % [2].

Для номинальных и порядковых признаков (доли объектов с заданным признаком)

.

где q=1–p,

p подбирается эмпирическим путем, или как крайний случай p=0,5 и q=0,5

При неизвестной численности генеральной совокупности для количественных признаков

для случая определения доли

.

Вид выборки. Стратифицированный способ отбора – все объекты разделяют на классы, именуемые слоями (стратами), в зависимости от изучаемых характеристик, таких как возраст, пол и т.п., после чего из каждого слоя отбирается простая случайная выборка с одинаковой или специально рассчитанной (для каждого слоя) выборочной долей

Объем генеральной совокупности известен

Признак количеcтвенный

Общий объем выборки определяется как

,

где – средняя внутригрупповая дисперсия; Ni – число объектов в каждом из классов генеральной совокупности

Тогда выборка из каждого класса имеет численность пропорциональную представительству в генеральной совокупности

.

Но более оптимальным является распределение выборки по классам с учетом вариабельности признака в этих классах

.

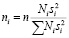Признак качественный (частота встречаемости)

,

где 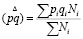– средняя внутригрупповая дисперсия,

где pi и qi – доля и обратная ей величина в каждом из классов генеральной совокупности (как крайний случай p=0,5 и q=0,5); Ni – число объектов в каждом из классов генеральной совокупности.

При неизвестной численности генеральной совокупности для количественных признаков

.

для случая определения доли

.

Разделение общей выборки по классам также производится пропорционально или с определенным весом.

Следует обратить внимание, что если доля выражается в относительных единицах, то все расчеты также производятся в относительных единицах, если в процентах – то и другие величины выражаются в процентах.

Кроме приведенных формул существуют и другие способы определения численности выборки. Среди них специальные таблицы и диаграммы, а также компьютерные программы. Учитывая, что в течение исследования неизбежны потери среди его участников (по разным причинам), рекомендуется расчетный объем выборки увеличить примерно на 20 %.

Обычно исследованию подлежат не один, а несколько признаков (например, давление, ЧСС, температура, биохимические показатели и т.д.), и для каждого признака возможен свой уровень значимости, клинически значимые изменения и, соответственно, свой объем выборки. В этом случае исследователь может в качестве окончательного выбрать наибольшую из всех рассчитанных численностей, или же задать объем выборки, рассчитанный для главного признака – исходя из основной гипотезы.

Рассмотрим данные методики на примерах.

Пример 1. Необходимо определить объем выборки при сравнении общего состояния в двух группах по шкале качества жизни SF-36 (Short Form-36). Разница считается статистически значимой при р<0,05. Заданная мощность критерия 85 %, минимально значимая разница по шкале SF-36 составляет 5 баллов. По результатам предварительного исследования стандартное отклонение в первой группе 9,1 балл, во второй – 10,2 балла.

.

С поправкой на возможность выбывания из исследования участников – 20 %, общий объем выборки составляет 86,4·1,2=104 участника, по 52 человека в каждой группе.

Пример 2. Рассчитаем объем выборки, необходимый для оценки урологической заболеваемости в некотором регионе с учетом того, что среди мужчин и женщин эта патология имеет различную распространенность. Общая численность взрослого населения в этом регионе (генеральная совокупность) составляет 1638240 человек, из них мужчин 735882 и женщин 902358 человек. По некоторым литературным данным урологические заболевания выявляются у 11,1 % мужчин и 10,7 % женщин (табл. 2).

Таблица 2

Сведения по урологической заболеваемости

Группа	Ni	pi, %	qi=(100 – pi), %	Δ, %	Z
Мужчины	735882	11,1	88,9	1	2,576
Женщины	902358	10,7	89,3

Нам необходимо сформировать стратифицированную выборку с учетом зависимости распространенности заболевания от пола. Т.к. ожидаемая доля невелика (~ 11 %) зададим ошибку доли 1 %.

Средняя внутригрупповая дисперсия

.

Общий объем выборки

чел.

При этом выборка мужчин

чел.

Выборка женщин

чел.

URL: https://www.applied-research.ru/ru/article/view?id=5074 (дата обращения: 14.04.2019).

 

[1] См. например, http://www.nickart.spb.ru/clause/text_17.php

[2] См. приложение 1 с примерами пояснения к таблице

[3] Полной наработкой является наработка изделия от начала некоторого этапа его эксплуатации до системного события, например, наработка до отказа.

[4] Неполная наработка характеризует наработку изделия: от начала эксплуатации до фиксированного момента времени

[5] Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака. Равномерному распределению признака соответствует на графике диагональ квадрата. При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.

 

[6] Примеры того, что отфильтровывается из видеопотока камер, чтобы улучшить распознавание изображений системами на основе нейросети: https://www.goal.ru/security-systems-video/100-tipov-video-pomekh-za-3-minuty/

[7] А/Б-тестирование (A/B testing) — метод исследования, при котором контрольная группа элементов сравнивается с набором тестовых групп, в которых один или несколько показателей были изменены, для того чтобы выяснить, какие из изменений улучшают целевой показатель;

[8] документация, описание, например, здесь: https://ru.wikibooks.org/wiki/%D0%AF%D0%B7%D1%8B%D0%BA_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_R/%D0%92%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5

[9] По данным: Бильгаева Л.П., Власов К.Г. ПРОГНОЗИРОВАНИЕ ПРОДАЖ В СРЕДЕ MATLAB // Естественные и математические науки в современном мире: сб. ст. по матер. XLIX междунар. науч.-практ. конф. № 12(47). – Новосибирск: СибАК, 2016. – С. 64-76.

[10] Корнеев С. В., директор PMCG Системы поддержки принятия решений // Источник: Журнал "Сети & Бизнес" (№6, 2005) размещено: 13.02.2006 http://www.management.com.ua/ims/ims096.html

[11] Группировочный признак - признак, по которому происходит объединение элементов выборки в группы – он должен отражать характерные черты изучаемого явления. Какой признак будет группировочным – решает экспериментатор.

[12] Доверительный интервал – диапазон разброса точечной оценки параметра, с учетом погрешности.

[13] Так, чем больше размер выборки, тем стат.ошибка меньше (она нивелируется). Пример: Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3%

[14] Ошибка репрезентативности, - погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность, рассчитывается по-разному для разных стат.показателей.

[15] Например, при некоторых значениях t статистики Стьюдента вероятности правильного вывода о равенстве параметра выборочной и генеральной таковы:

 Читается так: с вероятностью Р = 0,683 (68,3%) можно утверждать, что разность между выборочной и генеральной средней не превысит одной величины средней ошибки m (t = 1), с вероятностью Р = 0,954 (95,4%) — что она не превысит величины двух средних ошибок m (t = 2), с вероятностью Р = 0,997 (99,7%) — не превысит трех значений m (t = 3). Таким образом, вероятность того, что эта разность превысит трехкратную величину средней ошибки определяет уровень ошибки и составляет не более 0,3%. При n>30 степени вероятности безошибочного прогноза Р = 99,7% - соответствует значение t = 3, а при Р = 95,5% - значение t = 2.

Предыдущая123456789Следующая

Поделиться:

Воспользуйтесь поиском по сайту: