 |
Классификация доверительных интервалов и статистических погрешностей
|
|
|
|
По виду оцениваемого параметра:
1. Доверительный интервал для генерального среднего (математического ожидания); 
2. Доверительный интервал для дисперсии: 
где s2 - выборочная дисперсия; Χ2 - квантиль распределения Пирсона.
3. Доверительный интервал для среднеквадратического отклонения; 
4. Доверительный интервал для генеральной доли;

По типу выборки:
1. Доверительный интервал для бесконечной выборки;
2. Доверительный интервал для конечной выборки;
| Генеральная совокупность | Бесконечная | Конечная объема N |
| Тип отбора | Повторный | Бесповторный |
| Средняя ошибка выборки | 
| 
|
Выборка называется повторной, если отобранный объект перед выбором следующего возвращается в генеральную совокупность. Выборка называется бесповторной, если отобранный объект в генеральную совокупность не возвращается. На практике обычно имеют дело с бесповторными выборками.
Расчет средней ошибки выборки при случайном отборе
Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности.
Обозначения основных параметров генеральной и выборочной совокупности.
| Характеристики | Генеральная совокупность | Выборочная совокупность |
| Объем совокупности (численность единиц) | N | n |
| Численность единиц, обладающих обследуемым качеством (признаком) | M | m |
| Доля единиц, обладающих обследуемым качеством (признаком) | 
| 
|
Формулы расчета численности выборки при собственно-случайном способе отбора
| Способ отбора | Формулы определения численности выборки | |
| для средней | для доли | |
| Повторный | 
| 
|
| Бесповторный | 
| 
|
|
|
|
Найти численность выборки можно, использовав он-лайн калькулятор https://math.semestr.ru/group/interval.php
Потребуется указать значение ста.показателя (среднего выборочного или доли), точность расчетов и доверительную вероятность (обычно 0,95). Также играет роль тип выборки (с повторным отбором уже выбранных ранее элементов – или бесповторный отбор).
Начало формы
Для средней Для доли
Доля единиц w =. Точность ε =. Вероятность γ =
Бесповторный отбор
Конец формы
Алгоритм нахождения доверительного интервала включает следующие шаги:
1. задается доверительная вероятность γ (надежность).
2. по выборке определяется оценка параметра a.
3. из соотношения P(α1 < a < α2) = γ находится ошибка ε.
4. рассчитывается доверительный интервал (a - ε; a + ε).
Статистические графики - элементы графика, виды (диаграммы линейные, столбиковые, секторные, фигурные диаграммы, проч.).
Простейший способ анализа данных – изучение графиков, описывающих выборку и ее стат.характеристики в виде
- графиков сравнения в пространстве,
- графиков относительных величин (структуры, динамики),
- графики вариационных рядов,
- графики размещения по территории (статистические карты), например,

Элементы графика:
1. графический образ, отвечающий цели и сути данных.
2. краткий заголовок, пояснения шкал и элементов,
3. система координат (прямоугольные (простые и логарифмические), полярные)
4. масштабная шкала (система координат) диаграмм бывает прямолинейная или криволинейная, равномерной или неравномерной. Шкала начинается с 0 (обычно), а последнее число, наносимое на шкалу, превышает Хmax ряда. Если же одна или обе координатные оси начинаются не с нуля, то в начале координат наносятся два числа.
Самая распространенная система координат прямоугольн ая (декартов а) СК -горизонтальная ось (X) и вертикальная (Y):

Полярная система координат используется, если надо компактно показать динамику показателей во времени (сезонные и циклические колебания). Например, на диаграмме внизу слева – изменение мощности нагрузки энергосистемы страны на протяжении суток. Минимум нагрузки приходится на ночной интервал с 23 до 6 часов, а максимум на пиковый с 8 до 11 часов и с 20 до 22 часов.
|
|
|
Внизу справа – диаграмма колебаний спроса на какой-то явно сезонный товар.


Полярная система координат строится вокруг полюса - точки 0, и полярной оси ОХ. Изображение (кривая) выражается парой координат (радиус-вектор (расстояние) от полюса и угол между радиус—ветором и горизонтальной полярной осью).


Деления круга на сектора могут быть произвольными. Такая координатная сетка называется радиальной, а диаграммы в них - радиальными диаграммами. С их помощью изображают динамику показателей во времени, полный круг - период времени, например, год или 1 сутки.
Масштабная шкала прямоугольной С.К. может быть равномерной и неравномерной, например: Плоская линейная диаграмма с равномерной шкалой:
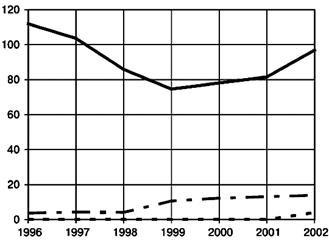
Из неравномерных шкал наибольшее распространение имеет десятичная логарифмическая шкала. - в ней интервалы пропорциональны логарифмам величин,.

- начало отсчета начинается не от 0, а от 1, так как lg 1=0, первое деление шкалы, соответствующее числу 2, будет расположено от начала отсчета шкалы на расстоянии 3,1, второе, соответствующее числу 3, - на расстоянии 4,77 и т. д. Если логарифмическая шкала нанесена на обе оси координат, то координатная сетка называется логарифмической, а если логарифмическая шкала нанесена только на одну из осей (обычно – ось ординат), координатная сетка называется полулогарифмической.
Чтобы облегчить построение и чтение диаграммы, через деления логарифмической шкалы обычно проводят прямые линии, координатную сетку.
Пример графика с полулогарифмической системой координат. - находим логарифмы для каждого уровня ряда. Определив минимальное и максимальное значение логарифмов, построим масштаб с таким расчетом, чтобы все данные разместились на графике.
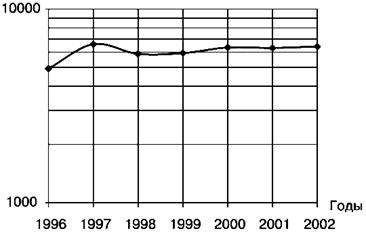
Применяя логарифмический масштаб, можно наглядно охарактеризовать динамику очень быстро, - экспоненциально - растущих во времени показателей (то, что называется «черные лебеди»).
|
|
|
Вогнутость говорит о падении темпов роста, выпуклость – говорит об увеличении темпа прироста.График с масштабной шкалой в виде логарифмов малодоступен для понимания, надо рядом с линиями логарифмов на масштабной шкале ставить числа, чтобы понять истинные темпы изменений процесса на логарифмической шкале.
|
|
|


