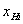|
А) Сначала надо определиться с числом групп.
|
|
|
|
(При чрезмерно широких интервалах группировки нельзя получить детальной картины распределения, поэтому возникает опасность упустить важные закономерные подробности формы распределения, а при группировке со слишком малым шагом каждый элемент приобретает чрезмерное большой вклад в поведение или свойства группы.)
· В случае многомерных выборок для разбиения на группы (кластеры), если неизвестно по какому принципу наилучшим образом разбить данные на группы - могут использоваться методы кластерного анализа (метод K-средних, EM-алгоритм, агломеративная (иерархическая или дивизионная) кластеризация и деревья классификации, DBSCAN-алгоритм, классифицирующие предварительно обученные нейросети). Некоторые из этих методов (например, деревья классификации) могут дать и оптимальное количество групп разбиения, если нужное число групп заранее неизвестно.
· Если выборки одномерная, и признак классификации известен, определяют оптимальное число групп исходя из целей или по правилу Стерджеса и т.п. Оптимальное число интервалов k исходя только из объема выборки n определяется одним из следующих способов:
1) по формуле Стерджеса: 
2) либо по таблице:
| Размер выборки, n | Рекомендуемое число интервалов группировки, k |
| 25—40 | 5—6 |
| 40—60 | 6—8 |
| 60—100 | 7—10 |
| 100—200 | 8—12 |
| Больше 200 | 10—15 |
Обычно интервалы классификации берут с одинаковым шагом по формуле: 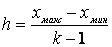 , где h – ширина интервалов, xмакс и хмин — максимальное и минимальное значение элемента выборки по таблице исходных данных (предварительно удобно упорядочить данные по возрастанию).
, где h – ширина интервалов, xмакс и хмин — максимальное и минимальное значение элемента выборки по таблице исходных данных (предварительно удобно упорядочить данные по возрастанию).
Длина интервалов:  может оказаться дробным числом. Правила округления h:
может оказаться дробным числом. Правила округления h:
ü Если интервал имеет один знак ДО запятой, то полученное значение округляется до десятых (0,88 = 0,9; 8,715 = 8,7)
|
|
|
ü Если величина интервала имеет два знака ДО запятой, то полученное значение округляется до целых (11,11 = 11; 29,98 = 30)
ü Если h получилось трех- и более- значным числом, то интервал принимают кратным 50 или 100
Размечаем границы групп (границы интервалов группировки), начиная с 1-го по принципу: н ижняя граница первого интервала выбирается так, чтобы минимум выборки приходился на середину первого интервала группировки:  .( для нижней границу XНi первого интервала).
.( для нижней границу XНi первого интервала).
Далее к этой величине прибавляем h, 2h, 3h, …, kh – и получаем НГ всех интервалов (групп).
Б) Распределяем исходные элементы выборки по группам, - кто куда попадает. Если какой то из элементов выборки попадает точно на границу интервалов группировки, экспериментатор решает, к какой группе отнести такие пограничные значения.
После того, как все элементы выборки разбиты на группы, начинается анализ групповых статистических величин, чтобы от исходной выборки составить новую выборку, состоящую из усредненных значений каждой группы:
- считаем середину каждого i-го интервала: 
- Считаем частот ы ni каждой группы – количество элементов выборки, попавших в каждую из групп. Сумма ni по всем группам должна совпасть с размером исходной выборки n.
- Вычисляем накопленн ые частот ы nxi для каждой из групп. Это число, полученное последовательным суммированием частот в направлении от первого интервала до последнего.
- Вычисляем относительную частоту fiкаждой группы  (отношение частоты группы к объему выборки). fi показывают долю (удельный вес) каждой группы в выборке.
(отношение частоты группы к объему выборки). fi показывают долю (удельный вес) каждой группы в выборке.
- Вычисляем накопленн ые относительные частост и Fi, по формуле  . Сумма всех частостей всегда равна 1.
. Сумма всех частостей всегда равна 1.
Заносим для каждой из k групп полученные статистические характеристики в таблицу – Это будет новый сгруппированный ряд данных:
|
|
|
Номер интервала
i
Границы интервалов
Срединные значения
xi
Частоты
ni
Накопл. частоты
nxi
Частости
fi
Накопл. относит.частоты
Fi