Множественное уравнение регрессии

В случае трехмерной модели системы случайных величин (X,Y,Z) уравнение, описывающее зависимость результативного признака от двух факторных признаков, определяемую статистически значимыми связями, имеет вид:

Z = g(x,y) + ε(x,y)

В качестве регрессии Z на (X,Y) обычно берется функция g(x,y), минимизирующая остаточную дисперсию как и сумму квадратов отклонений g(x,y) от истинной зависимости. Вид функции регрессии выбирается, а ее параметры определяются как решение задачи минимизации функции

S = M[ Z – g(x,y)]² = .

Если принята линейная модель регрессии, то определению подлежат три параметра функции g(x,y) = β₀ + β₁x + β₂y.

В случае нелинейной квадратической модели

и определению подлежат уже 6 параметров β, как управляемых переменных задачи оптимизации с целевой функцией S, которая должна достичь минимального при выбранном виде функции g(x,y) значения.

Проверку достоверности оценки функции регрессии по статистическим данным осуществляют с помощью коэффициента корреляции между значениями результирующего признака Z(x_i,y_i), вычисленными по найденной зависимости g(x_i,y_i), и статистическими значениями z_i. Если проверка проводится для разных видов модели регрессии, например линейной и квадратической, то по этим коэффициентам корреляции можно судить о том, какая из них лучше согласуется со статистическими данными.

Проверку значимости выборочной функции регрессии можно выполнить с помощью коэффициента детерминации, вычисляемого по выборке:

,

где ;

; ;

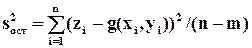n и m – объем выборки и число параметров функции регрессии. Для линейной модели m = 3, для квадратической m = 6. Выбирают ту модель, для которой коэффициент детерминации больше.

Оценку значимости полученного приближения функции регрессии в целом выполняют с помощью критерия Фишера.

 

Тесты для самоконтроля

Составьте краткие ответы на вопросы

1. Предмет и задачи многомерного статистического анализа – уровень2.
2. Функция распределения многомерной случайной величины – уровень 2.
3. Плотность распределения многомерной случайной величины – уровень 2.
4. Математическое ожидание компоненты многомерного случайного вектора – уровень 2.
5. Дисперсия компоненты многомерного случайного вектора – уровень 2.
6. Коэффициент ковариации двух компонент случайного вектора – уровень 2.
7. Коэффициент корреляции случайных величин – уровень 2.
8. Корреляционная матрица – уровень 2.
9. Коэффициент детерминации – уровень 1.
10. Частные коэффициенты корреляции – уровень 2.
11. Множественный коэффициент корреляции – уровень 2.
12. Условное распределение величины Z при заданном (x,y) – уровень 3.
13. Точечные оценки математических ожиданий составляющих трехмерной системы – уровень 2.
14. Точечные оценки дисперсий составляющих трехмерной системы – уровень 2.
15. Точечные оценки парных коэффициентов корреляции – уровень 2.
16. Точечные оценки частных коэффициентов корреляции – уровень 2.
17. Оценки условных средних квадратических отклонений – уровень 2.
18. Оценки множественных коэффициентов корреляции – уровень 2.
19. Проверка значимости множественного коэффициента детерминации – уровень 3.
20. Оценка уравнения линейной регрессии – уровень 3.
21. Функция регрессии Z на (X,Y) – уровень 3.
22. Линейная и нелинейная функции регрессии для трехмерной системы – уровень 2.
23. Определение параметров функции регрессии – уровень 3.
24. Проверка достоверности оценки функции регрессии – уровень 3.
25. Проверка значимости оценки функции регрессии – уровень 3.

 

 

Характеристика тестов

· всего вопросов – 25;

· количество вопросов уровня 1 – 1; уровня 2 – 17; уровня 3 – 7;

· количество баллов за вопрос:

§ уровня 1 – 1;

§ уровня 2 – 2;

§ уровня 3 – 3.

Количество баллов за раздел II – 56.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: