Общая схема проверки гипотез.

Ø Исходя из экономических соображений и содержания проблемы, формулируют нулевую гипотезу H₀.

Ø Задаются величиной уровня значимости критерия α, т.е. вероятностью отвергнуть правильную гипотезу H₀. Чем более правдоподобна гипотеза, тем меньше должно быть α: 0,05; 0,01; 0,005 и меньше. При наличии столь же правдоподобной альтернативной гипотезы H₁ уровень значимости следует выбирать равным вероятности ошибки второго рода (отвергнуть альтернативную гипотезу, когда она верна).

Ø Выбирают некоторую функцию – статистику ψ, зависящую от результатов наблюдений x₁,x₂, …, x_n, и находят законы ее распределения F_ψ(x) при обеих гипотезах H₀ и H₁. Это самый сложный этап с математической точки зрения.

Ø С помощью закона распределения F_ψ(x) на основе выбранного уровня значимости α область возможных значений статистики разбивают на области неправдоподобно малых и больших значений статистики ψ и область правдоподобных значений ψ.

Ø Вычисляют значение статистики ψ по статистическим данным выборки. Выясняют, в какую область попадает значение ψ(x₁,x₂, …, x_n) и принимают решение: если величина ψ попадает в область правдоподобия гипотезы H₀, то считают, что статистические данные не противоречат гипотезе H₀ и она принимается. Этому выводу всегда соответствуют вероятности ошибок α и β. Причем α = β, если две гипотезы априори одинаково правдоподобны.

В качестве статистик используют:

U или Z для нормально распределенных случайных величин;

F или V² дляраспределения по закону Фишера – Снедекора;

T для распределения Стьюдента;

χ² для распределения по закону χ² («хи квадрат»).

Проверку статистических данных на наличие «выбросов» осуществляют при большом объеме выборки с помощью статистики

S = (x^* - ) / σ

В качестве нулевой гипотезы H₀ выдвигается предположение: x^* – выброс. Значение S_кр определяется по таблице в зависимости от значений параметров: уровня значимости α и объема выборки n. Если S_набл > S_кр, гипотеза H₀ принимается, т.е. x^* – выброс. В противном случае гипотеза H₀ отвергается.

 

Тесты для самоконтроля

Составьте краткие ответы на следующие вопросы

1. Предмет математической статистики – уровень 1.
2. Две основные задачи математической статистики – уровень 1.
3. Вариационный ряд дискретной и непрерывной случайной величины – уровень 1.
4. Статистическое распределение и его виды – уровень 1.
5. Теоретическая и эмпирическая функции распределения – уровень 1.
6. Кривая распределения и гистограмма – уровень 1.
7. Плотность распределения вероятностей – уровень 1.
8. Числовые характеристики дискретных и непрерывных случайных величин – уровень 1.
9. Законы распределения непрерывных случайных величин – уровень 1.
10. Свойства нормального распределения – уровень 3.
11. Асимметрия и эксцесс нормального распределения – уровень 2.
12. Два способа оценки параметров распределения – уровень 2.
13. Требования к статистической оценке параметра распределения – уровень 2.
14. Точеные оценки числовых характеристик генеральной совокупности – уровень 2.
15. Интервальные оценки параметров распределения – уровень 2.
16. Что такое доверительная вероятность? – уровень 2.
17. Что такое доверительный интервал? – уровень 2.
18. Доверительные интервалы для неизвестного математического ожидания нормально распределенной случайной величины – уровень 3.
19. Что собой представляет задача статистической проверки гипотез? – уровень 2.
20. Основная и конкурирующая гипотезы – уровень 1.
21. Ошибки первого и второго рода при проверке статистических гипотез – уровень 2.
22. Что такое статистический критерий? – уровень 1.
23. Критическая область и критические точки – уровень 2.
24. Уровень значимости и критические точки – уровень 2.
25. Общая схема проверки гипотез – уровень 3.
26. Статистический критерий и проверка статистических данных на «выбросы»– уровень 3.

Характеристика тестов

· Всего вопросов – 26;

· Количество вопросов уровня 1 – 11; уровня 2 – 11; уровня 3 – 4.

· Количество баллов за вопрос

§ уровня 1 – 1;

§ уровня 2 – 2;

§ уровня 3 – 3.

Количество баллов за раздел 1 – 45.

 

 

II. Корреляционный и регрессионный анализ

Система случайных величин

 

Случайные величины, возможные значения которых определяются двумя и более числами, называются двумерными, трехмерными,…, n - мерными. Двумерная случайная величина обозначается (X, Y), а величины X и Y называют составляющими (компонентами). Обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. И, по аналогии, n – мерную величину можно рассматривать как систему n случайных величин. Различают дискретные и непрерывные многомерные случайные величины.

Законом распределения дискретной двумерной случайной величины называется перечень возможных значений этой величины, т.е. пар чисел (x_i,y_j), и их вероятностей p(x_i,y_j) (I = 1,2,…, n; j = 1,2,…,m). Обычно закон распределения задают в виде таблицы с двумя входами, в которой по строкам располагают значения Y, а по столбцам значения X, а в клетке, соответствующей (x_i,y_j), указывается вероятность p(x_i,y_j). Очевидно, что

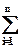
P(x_i) = ; P(y_j) = ; =1

Функцией распределения двумерной случайной величины (X,Y) называют функцию F(x,y), определяющую вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y:

F (x, y) = P (X < x, Y < y)

Функция распределения есть неубывающая функция по обоим аргументам, значения которой меняются в пределах от 0 до 1.

Плотностью совместного распределения вероятностей f (x, y) двумерной непрерывной случайной величины (X, Y) называют вторую смешанную частную производную от функции распределения

Плотность распределения одной из составляющих двумерной случайной величины находится по формуле:

f₁(x) = ; f₂(y) =

Для характеристики зависимости между составляющими двумерной дискретной случайной величины вводится понятие условного распределения. Если, допустим, в результате испытания величина Y приняла значение Y = y_j, при этом X примет одно из своих возможных значений x₁, x₂, …, x_n. Условная вероятность того, что X примет значение x_i при условии, что Y приняло значение y_j, обозначается так: p (x_i | y_j). Условным распределением составляющей X при Y = y_j называют совокупность условных вероятностей p(x_i | y_j)(i = 1,2,…,n), вычисленных в предположении, что событие

Y = y_j уже наступило. Аналогично определяется условное распределение составляющей Y. Зная закон распределения двумерной случайной величины, можно найти условные законы распределения составляющих:

p (x_i | y_j) = p(x_i,y_j) / p (y_j); p (y_j | x_i) = p(x_i, y_j) / p (x_i)

Сумма вероятностей условного распределения равна 1: .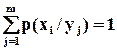

Условной плотностью φ (x | y) распределения составляющих X при данном значении Y = y называют отношение плотности совместного распределения f (x, y) системы (X, Y) к плотности распределения f₂ (y) составляющей Y: f(x | y) = f(x, y) / f₂ (y)

и аналогично определяется условная плотность распределения составляющей Y при данном значении X = x:

f(y | x) = f(x, y) / f₁ (x)

Отличие условной плотности f(x | y) от безусловной плотности f₁(x) состоит в том, что функция f(x | y) дает распределение X при условии, что составляющая Y приняла значение Y = y; функция f₁(x) дает распределение X независимо от того, какие из возможных значений приняла составляющая Y. Аналогичные рассуждения справедливы и для условной и безусловной плотности f(y | x) и f₂ (y).

Условным математическим ожиданием дискретной случайной величины Y при X = x, где x – определенное возможное значение X, называют сумму произведений возможных значений Y на их условные вероятности: M (Y | X = x) =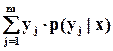

Для непрерывной случайной величины

M (Y | X = x) = ,

где f(y | x) – условная плотность случайной величины Y при X = x. Аналогично определяется условное математическое ожидание X при Y=y.

Условное математическое ожидание M(Y | x) является функцией от x: M (Y | x) = f (x), которую называют функцией регрессии Y на X. Аналогично определяется условное математическое ожидание случайной величины X и функция регрессии X на Y: M (X | y) = φ (y).

Для описания системы двух случайных величин, кроме числовых характеристик составляющих, используют корреляционный момент и коэффициент корреляции.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: