Нелинейная корреляционная связь

Тесноту связи между X и Y удобно оценивать в единицах общей дисперсии σ_y, т.е. рассматривать отношение остаточной дисперсии к дисперсии признака относительно его математического ожидания:

{M[ 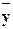_x – M(Y) ]²} / σ_y²

Эту величину называют теоретическим корреляционным отношением η²_Y|x.

Для оценки тесноты линейной корреляционной связи между признаками в выборке служит выборочный коэффициент корреляции. Для оценки тесноты нелинейной корреляционной связи вводят новые сводные характеристики: η_yx и η_xy – выборочные корреляционные отношения Y к X и X к Y.

Выборочным корреляционным отношением Y к X называют отношение:

R_yx = s 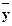_x / s_y,

где s 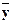_x = ; s_y = ;

n_x – частота значения x признака X; n_y – частотазначения y признака Y;

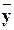– общая средняя признака Y; _x – условная средняяпризнака Y.

Аналогично определяется выборочное корреляционное отношение X к Y: R_xy = s _y / s_x

Однако чаще пользуются коэффициентом детерминации

R² = s²_факт / s²_общ ,

который является отношением объясненной с помощью функции регрессии части дисперсии к общей дисперсии. Коэффициент детерминации определяет долю рассеивания величины Y, обусловленную функциональной зависимостью ее от величины X. Величина

1 – R² = s²_ост / s²_общ

Показывает, какую долю рассеивания случайной величины Y обуславливают случайные факторы.

Свойства коэффициента детерминации:

· 0 ≤ R² ≤ 1;

· если R² = 0 (η = 0), признак Y с признаком X корреляционной зависимостью не связан;

· если R2 =1 (η =- 1), признак Y связан с признаком X функциональной зависимостью;

· R ≥ │r_в │ ивыборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции: η ≥ │r_в │;

· если R = │r_в │, то имеет место точная линейная корреляционная зависимость, т.е. точки (x_i,y_i) лежат на прямой линии регрессии, найденной МНК.

С возрастанием R² корреляционная связь становится более тесной, так

как уменьшается (1 – R²), т.е. уменьшается дисперсия, вызванная воздействием неучтенных факторов.

Преимущество корреляционного отношения перед коэффициентом

корреляции состоит в том, что оно служит мерой тесноты связи любой, в том числе и линейной, формы. Однако, оно не позволяет судить, насколько близко расположены точки наблюдений к кривой определенного вида (параболе, гиперболе и т.д.).

Если график регрессии изображается кривой линией, то корреляцию называют криволинейной. В общем случае нелинейная модель регрессионного анализа имеет вид:

y = g(x₁,x₂,…,x_k) + ε(x₁,x₂,…,x_k),

где g(x₁,x₂,…,x_k) – нелинейная функция регрессии Y на (x₁,x₂,…,x_k); ε(x₁,x₂,…,x_k) – отклонение, погрешность замены истинной зависимости функцией регрессии. В случае двумерной случайной величины функция регрессии

g(x) = β₀ + β₁x + β₂x².

Параметры β₀, β₁ и β₂ определяются как значения, при которых остаточная

дисперсия регрессии Y на X S_{ост =} становится минимальной.

Оценку значимости приближения функций регрессии выполняют с помощью критерия Фишера:

F_расч = ,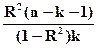

где k – количество факторных признаков (k = 1 для двумерной модели).

Если F_расч > F_кр, гипотеза H₀: уравнение регрессии не значимо отвергается и уравнение считается не противоречащим статистическим данным. В противном случае, когда F_расч < F_кр, гипотеза принимается. Значение F_кр(m₁,m₂,α) находится по таблице в зависимости от количества факторных признаков k

(m₁ = k), объема выборки n (m₂ = n) и уровня значимости α (0,05).

 

Тесты для самоконтроля

Составьте краткие ответы на вопросы

1. Двумерная случайная величина и законы ее распределения – уровень 2.
2. Условная вероятность и условное распределение – уровень 2.
3. Условное математическое ожидание и функция регрессии – уровень 2.
4. Корреляционный момент и коэффициент корреляции – уровень 2.
5. Выборочный коэффициент корреляции – уровень 2.
6. Коррелированные и не коррелированные случайные величины – уровень 1.
7. Проверка значимости коэффициента корреляции – уровень 3.
8. Доверительный интервал для коэффициента корреляции – уровень 3.
9. Среднеквадратическая регрессия Y на X – уровень 3.
10. Остаточная дисперсия Y относительно X – уровень 3.
11. Условное среднее – уровень 1.
12. Выборочное уравнение регрессии – уровень 2.
13. Оценка параметров уравнения прямой линии регрессии – уровень 3.
14. Оценка значимости коэффициентов регрессии – уровень 3.
15. Оценка значимости линейной функции регрессии – уровень 3.
16. Доверительный интервал для значимых параметров – уровень 3.
17. Основное назначение и идея дисперсионного анализа – уровень 2.
18. Факторная и остаточная дисперсия – уровень 3.
19. Оценка тесноты нелинейной корреляционной связи – уровень 2.
20. Коэффициент детерминации и его свойства – уровень 3.
21. Нелинейная функция регрессии – уровень 2.
22. Оценка значимости нелинейной функции регрессии для двумерной системы – уровень 3.

Характеристика тестов

· всего вопросов – 22;

· количество вопросов уровня 1 – 2; уровня 2 – 9; уровня 3 – 11;

· количество баллов за вопрос:

§ уровня 1 – 1;

§ уровня 2 – 2;

§ уровня 3 – 3.

Количество баллов за раздел II – 53.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: