Регрессионный анализ двумерной модели.

 

В среде Excel для двумерного случая линейной регрессии предусмотрено несколько инструментов: статистические функции (КОРРЕЛ, ЛИНЕЙН, ТЕНДЕНЦИЯ и др.); инструмент Регрессия надстройки Пакет анализа; графические средства при работе с диаграммой – построение линии тренда.

С помощью Пакета анализа можно получить искомую информацию, следуя такому алгоритму:

– разместить на рабочем листе Excel в двух смежных столбцах с соответствующими заголовками статистические данные по двум признакам, подлежащим исследованию (например, X4 и X6);

– Сервис – Анализ данных – Регрессия;

– в появившемся диалоговом окне Регрессия ввести входные данные в поля Входной интервал Y (X6)и Входной интервал X (X4)и щелкнуть по полю Метки, чтобы заголовки не вошли в интервалы данных;

– ввести параметры вывода в поле Выходной интервал: адрес левого верхнего угла таблицы результатов или щелкнуть поле Новый рабочий лист для вывода на другой лист (см. рис.4);

– для наглядности можно вывести график, щелкнув по полю График подбора;

– OK.

 

 

Рис.4.Работа с диалоговым окном Регрессия.

 

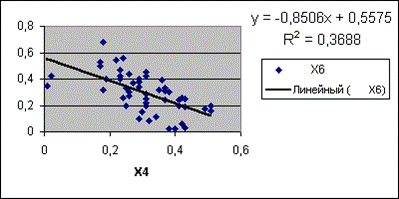
Результат работы инструмента Регрессия приведен на рис.5. Итак, выборочное уравнение линейной регрессии X6 на X4 имеет вид:

Выходная таблица содержит коэффициент детерминации R² = 0,368802, что означает, что полученная модель приблизительно на 37% отражает зависимость X6 от X4.

Стандартная ошибка (отклонение результата) = 0,118415 означает, что 68% реальных значений результирующего признака x₆ находится в диапазоне 0,118415 от линии регрессии. Это следует из того, что условные распределения нормально распределенной генеральной совокупности при фиксировании различных подмножеств компонент являются нормальными.

В разделе Дисперсионный анализ приведены значения таких величин:

df – число степеней свободы; SS –сумма квадратов отклонений; MS – дисперсия; F – расчетное значение F–критерия. Поскольку критическое значение критерия Фишера F_кр = 4,03 (m₁=1; m₂=50; ) F_расч =28,63 > F_кр , и, следовательно с вероятностью гипотеза об отсутствии связи между рассматриваемыми признаками отвергается. Это означает, что уравнение в целом статистически значимо, т.е. хорошо соответствует данным наблюдений.

 

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,607291
R-квадрат	0,368802
Нормированный R-квадрат	0,35592
Стандартная ошибка	0,118415
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,401452	0,401452	28,63014	2,3E-06
Остаток		0,687078	0,014022
Итого		1,088529
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	0,557512	0,051111	10,90789	1,04E-14	0,45480	0,66022
X4	-0,85062	0,158973	-5,35071	2,3E-06	-1,1701	-0,5312

 

Рис.5. Результаты регрессионного анализа.

 

Нижняя часть таблицы содержит такие сведения:

Коэффициенты – оценки параметров 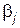уравнения регрессии;

Стандартная ошибка – стандартные отклонения ;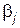

t–статистика – расчетное значение. Таким образом, можно оценить значимость коэффициентов уравнения регрессии, сравнив расчетное значение t – статистики с критическим значением, найденным по распределению Стьюдента при уровне значимости и m=50: t_кр =2,009. Поскольку 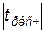> t_кр для обоих коэффициентов, то они являются статистически значимыми при уровне доверительной вероятности 0,95.

Нижние 95% и Верхние 95% определяют нижние и верхние границы доверительных интервалов для коэффициентов уравнения регрессии при . Поскольку доверительные интервалы не содержат 0, это подтверждает значимость коэффициентов уравнения регрессии.

Для получения линии регрессии и ее уравнения в случае двумерной модели удобным инструментом Excel является добавление линии тренда к точечной диаграмме, построенной на значениях компонент системы двух заданных случайных величин как результатов наблюдения (см. рис.6).

 

X4	X6
0,01	0,35
0,02	0,42
0,17	0,5
0,17	0,53
0,18	0,68
0,18	0,32
0,19	0,4
0,22	0,54
0,23	0,4
0,23	0,42
0,23	0,47
0,23	0,4
0,24	0,56
0,24	0,26
0,25	0,2
0,25	0,33
0,26	0,44
0,26	0,3
0,26	0,27
0,27	0,37
0,29	0,38
0,29	0,34
0,29	0,1
0,29	0,4

Рис. 6. Линии тренда.

Алгоритм содержит такие действия:

– разместить на рабочем листе Excel в двух смежных столбцах исходные данные таким образом, чтобы первым был независимый показатель;

– Вставка – Диаграмма – Точечная (первый вариант) – Далее;

– на закладке Диапазон данных ввести диапазон, занимаемый всей таблицей, для чего выделить мышью оба столбца;

– на закладке Ряд ввести в поле Значения X диапазон значений независимой величины, а в поле Значения Y диапазон значений величины, регрессию которой следует оценить (см.рис.7);

– Далее – на закладке Заголовки ввести заголовки осей и диаграммы – Далее – указать, где разместить диаграмму (на имеющемся листе) – Готово;

– откорректировать появившуюся диаграмму, особенно формат осей и надписи, для чего щелкнуть правой кнопкой мыши по оси или надписи и в появившемся маленьком диалоговом окне щелкнуть по пункту Формат оси (или надписи);

– в появившемся диалоговом окне Формат оси (или надписи) выбрать нужную закладку и внести необходимые изменения – OK;

– откорректировать полученное корреляционное поле, исключив резко выделяющиеся из общего множества отдельные точки;

 

Рис.7. Построение корреляционного поля.

 

– щелкнуть правой кнопкой мыши по любой точке диаграммы и в появившемся диалоговом окне выбрать пункт меню Добавить линию тренда;

– в появившемся диалоговом окне на закладке Тип выбрать тип зависимости: линейный или полиномиальный (указать порядок приближения);

– щелкнуть по закладке Параметры и в появившемся после этого диалоговом окне щелкнуть пункты показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2);

– записать уравнение регрессии, заменив y и x на имена результативного и факторного признаков соответственно и оценить значимость полученного уравнения с помощью R^2.

На рис.6 приведены: точечная диаграмма зависимости X6 от X4 и две линии тренда – линейная и нелинейная. Уравнение первой совпадает с уравнением линии регрессии, полученным с помощью инструмента Регрессия. Вторая имеет уравнение, т.е. оценку линии регрессии, такого вида:

.

Причем коэффициент детерминации в первом случае равен 0,3688, а для кубической зависимости R² = 0,4762, т.е. предпочтительнее использовать полиномиальную зависимость как лучше согласующуюся со статистическими данными.

Для остальных двух отобранных пар факторных признаков необходимо выполнить такие же действия и получить аналогичные оценки функций регрессии.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: