Выборочное уравнение регрессии

Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе или одна из двух величин подвержены еще воздействию случайных факторов. Причем среди этих факторов могут быть и общие для обеих величин, т.е. воздействующие на обе случайные величины. В этих случаях возникает статистическая зависимость.

Статистической называется зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, изменение одной из величин вызывает изменение среднего значения другой. В этом случае статистическая зависимость называется корреляционной. Например, связь между количеством удобрений и урожаем, между вложенными средствами и прибылью.

Среднее арифметическое наблюдавшихся значений случайной величины Y, соответствующих значению X=x, называется условным средним 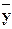_x и является точечной оценкой математического ожидания. Аналогично определяется условное среднее 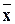_y.

Условное математическое ожидание M (Y | x) является функцией от x, следовательно, его оценка, т.е. условное среднее 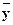_x, также функция от x:

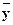_x = f*(x).

Это уравнение называется выборочным уравнением регрессии Y на X. Функцию f*(x) называют выборочной регрессией, а ее график – выборочной линией регрессии Y на X. Аналогично уравнение

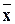_y = φ^* (y),

функцию φ^* (y) и ее график называют выборочным уравнением регрессии, выборочной регрессией и выборочной линией регрессии X на Y.

Отыскание параметров функций f*(x) и φ ^* (y), если вид их известен, оценка тесноты связи между величинами X и Y – задачи корреляционного анализа. Задачей регрессионного анализа есть оценка параметров функции регрессии β_i и остаточной дисперсии σ_ост².

Остаточная дисперсия – та часть рассеивания Y, которую нельзя объяснить действием X. σ_ост² может служить для оценки точности подбора функции регрессии и полноты набора признаков, включенных в анализ. Вид зависимости g(x) выбирают, исходя из характера поля корреляции и природы процесса.

Оценкой коэффициента линейной регрессии β является выборочный коэффициент регрессии Y на X r_yx. Значения параметра r _yx и параметра b уравнения прямой линии регрессии

Y = r_yx x + b

подбираются таким образом, чтобы точки (x₁,y₁), (x₂,y₂),…,(x_n,y_n), построенные по данным наблюдений, на плоскости xOy лежали как можно ближе к прямой линии регрессии. Это равносильно требованию, чтобы сумма квадратов отклонений функции Y(x_i) от y_i была минимальной. В этом суть МНК.

Выборочное уравнение прямой линии регрессии Y на X может быть записано в таком виде:

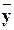_x – 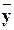= r_в s_y/s_x (x – ),

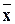где s_x и s_y – выборочные средние квадратические отклонения X и Y, а

r_в = –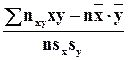

выборочный коэффициент корреляции, вычисленный по сгруппированным данным. Здесь n_xy – частота пары вариант (x,y). Аналогично находят выборочное уравнение прямой линии регрессии X на 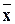Y:

_y – 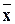= r_в s_x/s_y (y – )

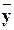Для того, чтобы установить, соответствует ли найденная по выборке математическая модель зависимости между Y и X статистическим данным, следует оценить значимость коэффициентов регрессии и значимость уравнения регрессии.

Проверить значимость коэффициентов регрессии означает установить, достаточна ли величина оценки для обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Выдвигают гипотезу H₀: коэффициент регрессии равен нулю β =0. Проверку гипотезы H₀ осуществляют с помощью распределенной по закону Стьюдента статистики

t = │b / s_b│

где b – оценка коэффициента регрессии, а s_b – оценка его среднего квадратического отклонения, другими словами стандартная ошибка оценки. Если │t │≥ t_кр (α, k), нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, и коэффициент считают значимым. При │t │< t_кр нет оснований отвергать нулевую гипотезу.

Оценки среднего квадратического отклонения коэффициентов регрессии вычисляют по формулам:

s_β0 = s_ост / 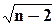; s_β1 = s_ост / (s_x ),

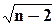где s_x = ,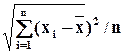

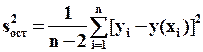– оценка остаточной дисперсии.

Доверительный интервал для значимых параметров строится по обычной схеме:

b – t(α,k)s_b < β < b + t(α,k)s_b.

Проверить соответствие математической модели зависимости Y от X статистическим данным следует с помощью оценки значимости самого уравнения регрессии. Оценку значимости приближения функции регрессии в целом выполняют с помощью критерия Фишера, для чего сравнивают c F_кр значение статистики

F_расч =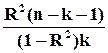

Здесь R² – коэффициент детерминации, n – объем выборки, k – количество факторных признаков.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: