III.Многомерный статистический анализ

Использование методов многомерного статистического анализа является особенно необходимым в условиях, когда решения принимаются на основании анализа стохастической, неполной информации, что имеет место при изучении социально-экономических процессов и явлений, зависящих от большого числа параметров.

В многомерном статистическом анализе изучают генеральные совокупности с точки зрения нескольких признаков. Объекты исследования: случайный вектор (или точка) X(x₁,x₂,…,x_k) в k –мерном евклидовом пространстве; система k случайных величин; k-мерная случайная величина.

Одним из важнейших результатов применения многомерного статистического анализа является статистический вывод о параметрах или характеристиках генеральной совокупности.

 

Основные характеристики многомерной генеральной совокупности

Функция распределения случайного вектора X(x₁,x₂,…,x_k)

F(x) = P(X₁<x₁,X₂<x₂;…;X_k<x_k)

является детерминированной неотрицательной величиной и обладает свойствами, аналогичными свойствамфункции распределения одной случайной величины. Для непрерывного случайного вектора функция распределения выражается через плотность распределения ρ(x) = ρ(x₁,x₂,…,x_k)≥0

К основным числовым характеристикам относятся: математическое ожидание j-ой компоненты M(x_j) вектора X; начальный смешанный момент 2-го порядка M(x_i,x_j) (i≠j); центральный момент 2-го порядка

–

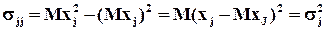дисперсия j-ой компоненты; центральный смешанный момент 2-го порядка

–

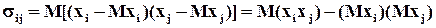коэффициент ковариации i-ой и j-ой компонент вектора X (i≠j).

Коэффициент ковариации нормированных случайных величин называется коэффициентом корреляции ( или коэффициентом парной корреляции):

,

где σ_i,σ_j – средние квадратические отклонения x_i и x_j. 0≤ ρ_ij ≤1. Матрица, составленная из коэффициентов парной корреляции, симметрична и называется корреляционной матрицей:

Квадрат коэффициента корреляции называется коэффициентом детерминации и определяет тоже степень тесноты связи между случайными величинами. Однако коэффициенты корреляции непосредственными измерителями связи между компонентами случайного вектора при k > 2 быть не могут. Они играют важную вспомогательную роль при вычислении действительных показателей связи между признаками генеральной совокупности и в образовании различных моделей многомерного статистического анализа.

 

Множественная корреляция

Корреляционная связь между несколькими признаками при k > 2 называется множественной. Простейшим случаем является трехмерная модель. Трехмерная случайная величина (X,Y,Z), распределенная по нормальному закону, характеризуется девятью параметрами:

– математическими ожиданиями Mx, My, Mz;

– дисперсией Dx, Dy, Dz;

– парными коэффициентами корреляции ρ_xy, ρ_xz, ρ_yz.

Через эти параметры выражаются частные коэффициенты корреляции, которые определяются при фиксированных значениях остальных случайных величин:

Аналогично определяются частные коэффициенты корреляции ρ_xz/y и ρ_yz/x.

Для нормального распределения частный коэффициент корреляции ρ_xy/z совпадает с парным коэффициентом корреляции между X и Y при фиксированном Z в двумерном условном распределении (X,Y)/Z и обладает всеми его свойствами. Частный коэффициент корреляции служит показателем линейной связи между двумя переменными случайными величинами независимо от влияния остальных случайных величин. Для оценки тесноты связи используют и коэффициент детермина ции, равный квадрату коэффициента корреляции.

Если частный коэффициент детерминации меньше, чем соответствующий парный коэффициент детерминации, то взаимосвязь между двумя величинами обусловлена частично (или целиком при равенстве нулю частного коэффициента детерминации) воздействием на эту пару остальных, фиксируемых, случайных величин. Если же, наоборот, частный коэффициент детерминации больше соответствующего парного коэффициента детерминации, то фиксируемые величины ослабляют связь.

Множественный коэффициент корреляции между одной величиной Z и двумя другими величинами (X,Y) определяется по формуле:

и является мерой связи между одной случайной величиной и двумя остальными. Множественный коэффициент детерминации, равный , показывает долю дисперсии случайной величины Z, обусловленную изменением случайных величин (X,Y).

Значения множественного коэффициента корреляции заключены между 0 и 1: 0 ≤ ρ_z≤ 1. При ρ_z = 1 связь между Z и (X,Y) является функциональной. Точки (x,y,z) расположены в плоскости регрессии Z на (X,Y). Если ρ_z = 0, то одномерная случайная величина Z и двумерная случайная ве личина (X,Y) являются независимыми (в силу нормальности их распределения). При этом .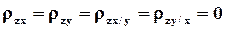

В случае многомерной модели случайной величины особое значение имеют условные распределения. Для трехмерной модели это – условное распределение при фиксированном z и условное распределение при заданном (x,y).

При заданном z получаем двумерное распределение (x,y)/z, которое определяется при нормальном распределении пятью параметрами: двумя условными математическими ожиданиями μ_x/z и μ_y/z; двумя условными дисперсиями σ²_x/z и σ²_y/z; условным коэффициентом корреляции ρ_xy/z.

Распределение z/(x,y) является одномерным и определяется своими условным математическим ожиданием Mz/(x,y) и условной дисперсией Dz/(x,y) = σ²_z/xy. Если точку (x,y) менять, то получим плоскость регрессии z на (x,y)

Mz/(x,y) – μ_z = β_zx/y(x – μ_x) + β_zy/x(y – μ_y)

и остаточную дисперсию относительно плоскости регрессии, совпадающую с условной дисперсией

σ²_z/xy = σ²_z/x(1 – ρ²_zx/y) = σ²_z/x(1 – ρ²_yz/x).

β_zx/y и β_zy/x – коэффициенты множественной регрессии. Множественный коэффициент корреляции ρ_z можно вычислить в силу линейности регрессии и как корреляционное отношение z на (x,y):

 

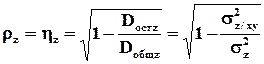
Точечные оценки частных и множественных коэффициентов корреляции вычисляются по выборке и выражаются через оценки основных числовых характеристик. Оценками математических ожиданий служат выборочные средние:

Оценки дисперсий – выборочные дисперсии:

,

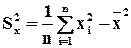
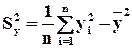
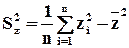где S_x, S_y, S_z – оценки средних квадратических отклонений.

Оценки парных коэффициентов корреляции:

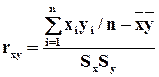
r_xz и r_yz определяются аналогично.

Оценка частного коэффициента корреляции:

(аналогично для всех остальных).

Оценки условных средних квадратических отклонений:

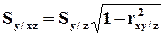
Оценки множественных коэффициентов корреляции:

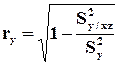
Проверка значимости множественного коэффициента детерминации ρ_z² осуществляется с помощью F-распределения. Вычисляется

F_набл =

Затем с уровнем значимости α и числами степеней свободы ν₁=2 (числителя) и ν₂ = n – 3 (знаменателя) находят F_кр. Если F_набл > F_кр, гипотеза H₀: ρ_z² = 0 отвергается с вероятностью ошибки α, т.е. ρ_z² значимо отличается от 0. В противном случае, если коэффициент ρ_z незначим, связь между случайной величиной Z и случайной величиной (X,Y) отсутствует.

Для значимых множественных коэффициентов корреляции можно получить оценки уравнения регрессии. Так, если ρ_z значимо отличается от нуля, оценкой соответствующего уравнения регрессии будет

.

При этом коэффициенты регрессии вычисляются по формулам:

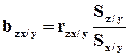
и является оценкой Mz/(x,y).

Для значимых параметров связи можно найти интервальную оценку с надежностью γ = 1 – α с помощью Z–преобразования Фишера.

 

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: