 |
Проверка закона распределения.
|
|
|
|
Предварительный анализ статистических данных заключается в проверке соответствия их предположению о нормальном распределении параметров, для чего строится гистограмма и определяются выборочные числовые характеристики. Для построения гистограммы необходимо выполнить такую последовательность действий:
– разместить на рабочем листе Excel статистические данные наблюдений (без выбросов);
– Сервис – Анализ данных – Гистограмма (рис.1);
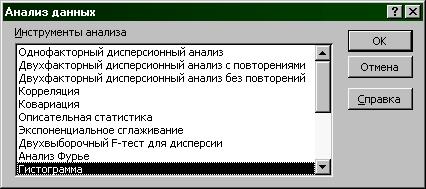
Рис.1.Выбор инструмента анализа.
– в появившемся диалоговом окне Гистограмма ввести в поле Входные данные интервал (диапазон) ячеек, содержащий исходные данные, и отметить поле Метки, если таблица данных имеет заголовки;
– ввести в поле Параметры выхода адрес ячейки, с которой должны размещаться выходные данные (выходной интервал) и щелкнуть пункт Вывод графика;
– OK.
Гистограммы необходимо построить для всех признаков статистических данных и сравнить их с кривой нормального распределения с целью убедиться, что закон распределения каждого признака близок к нормальному, как на приведенной гистограмме.
Числовые характеристики для всех признаков оцениваются по выборке с помощью инструмента анализа Описательная статистика., вызов которого осуществляется аналогично (см. рис.1). В появившемся диалоговом окне Описательная статистика необходимо ввести таким же образом Входные данные и Параметры вывода, только вместо пункта Вывод графика следует отметить пункт Итоговая статистика.
Результаты применения инструмента Описательная статистика к данным наблюдений по результативному признаку Y2 и выбранным факторным признакамприведены ниже (Рис.2).
| Y2 | X4 | X5 | X6 | X7 | X8 | |
| Среднее | 86,76959 | 0,316531 | 0,730612 | 0,299592 | 1,321224 | 0,984286 |
| Стандартная ошибка | 8,947579 | 0,013529 | 0,007339 | 0,022097 | 0,0173 | 0,066061 |
| Медиана | 68,6 | 0,31 | 0,73 | 0,3 | 1,35 | 0,88 |
| Мода | #Н/Д | 0,31 | 0,78 | 0,2 | 1,35 | 0,67 |
| Стандартное отклонение | 62,63305 | 0,094705 | 0,051373 | 0,154677 | 0,1211 | 0,46243 |
| Дисперсия выборки | 3922,899 | 0,008969 | 0,002639 | 0,023925 | 0,014665 | 0,213842 |
| Эксцесс | 0,972081 | 0,898188 | -0,63168 | -0,11908 | -0,62273 | 0,452437 |
| Асимметричность | 1,343112 | -0,25034 | -0,26748 | 0,228867 | -0,07536 | 0,622524 |
| Интервал | 251,2 | 0,49 | 0,21 | 0,66 | 0,52 | 2,17 |
| Минимум | 13,6 | 0,02 | 0,62 | 0,02 | 1,09 | 0,03 |
| Максимум | 264,8 | 0,51 | 0,83 | 0,68 | 1,61 | 2,2 |
| Сумма | 4251,71 | 15,51 | 35,8 | 14,68 | 64,74 | 48,23 |
| Счет |
|
|
|
Рис.2. Описательная статистика
Как видно, результаты Описательной статистики дают возможность оценить справедливость предположения о нормальном распределении признаков: эксцесс и асимметричность невелики, хотя и отличаются от 0. Нормальный закон распределения факторных признаков подтверждается еще и тем, что значения медианы и моды у них совпадают или близки.
Корреляционный анализ
Предварительный анализ тесноты взаимосвязи параметров многомерной модели осуществляется по оценке корреляционной матрицы генеральной совокупности X по наблюдениям. Для этого используется инструмент Анализ данных в соответствии со следующим алгоритмом:
– разместить на рабочем листе Excel статистические данные в столбцах с соответствующими заголовками (именами переменных);
– Сервис – Анализ данных – Корреляция;
– в появившемся диалоговом окне Корреляция в соответствующие поля ввести с помощью мыши входные данные и параметры вывода (см. рис.3);
– после щелчка мышью по кнопке OK на рабочем листе появится матрица, содержащая оценки парных коэффициентов корреляции.
– Отобрать для дальнейшего анализа пары переменных, имеющие наибольшие значения парных коэффициентов корреляции
(
0,4), учитывая, что чем меньше коэффициент rij, тем слабее их связь. Такими парами в приведенном примере (рис.3) являются: Y2–X4; Y2–X8; X4–X6; X5–X7; X7–X8. Причем признак X4 связан со всеми другими компонентами с отрицательным коэффициентом корреляции. Это говорит об обратной зависимости, что вполне естественно для трудоемкости единицы продукции и других показателей.
|
|
|
– Проверить значимость коэффициентов корреляции на уровне 
= 0,05. Поскольку объем выборки для всех признаков одинаков и равен 53, критическое значение r кр для всех пар будет одинаково и в соответствии с таблицей Фишера–Иейтса r кр = r табл (0,05;53)< r табл(0,05;50) = 0,273. Поскольку для всех коэффициентов выполняется неравенство 
> r кр , коэффициенты корреляции всех отобранных пар признаков значимо отличаются от нуля, что подтверждает связь между ними.
Дальнейший анализ статистических данных зависит от размерности принимаемой модели. Простейший вариант – двумерная модель. Учитывая, что в приведенном примере Y2 – результирующий признак, входящий в две пары, следует рассмотреть трехмерную модель Y2–X4–X8. В остальных парах следует определить зависимости между X6 и X4, X7 и X8, X5 и X7.
Таким образом, следует установить зависимости: Y2 = F(X4,X8);
X6 = φ(X4); X8 = φ(X7); X5 = φ(X7).
Рис.3.Анализ парной корреляции.
|
|
|
