Принятие решений в сельском хозяйстве

Задача 8.2. Планирование участков земли под картофель, проводимое методом Байеса. При наличии больших массивов земли в хозяйстве можно сознательно выбирать наиболее выгод­ные для урожая участки с учетом их влажности.

В период вегетации требуется определенное количество вла­ги. Если влажность будет излишняя, то часть посадочного мате­риала начнет гнить, урожай будет плохим.

Картофель в средней полосе сажают обычно в апреле. В это время трудно предвидеть, каким будет лето - сухим или влаж­ным. Фактически создается ситуация, которую можно считать игрой с природой. Мы должны принять решение, на каких уча­стках сажать картофель: на сухих или на тех, которые сами по себе являются влажными.

Введем условные обозначения:

W = {Q₁, Q₂} - множество состояний природы;

Q₁ - осадки выше нормы;

Q₂ – сухое лето (осадки не выше нормы);

А = { а₁, a₂ } - множество решений статистика;

а₁ - посадку производить на участках с большой влажностью почвы;

a₂ - посадку производить на сухих участках, так как ожида­ется влажное лето.

Известны средние урожаи в зависимости от принятого реше­ния и состояния природы. При этом наименьшие урожаи быва­ют, если осадки выше нормы (Q₁), и принимается решение а₁ -сажать картофель на влажных участках.

Наибольшие урожаи в среднем бывают при решении а₂ -сажать картофель на сухих участках и при состояниях природы Q₁ - влажное лето.

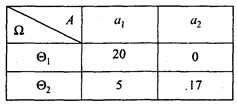
Прибыль на 1 га в тыс. руб. в среднем известна по многолет­ним результатам (табл. 8.5).

Таблица 8.5

 

Итак, мы получили значения прибыли, а нас интересуют потери.

Решение. Представим функцию потерь L (Q, a) в виде разно­сти между наибольшей прибылью и прибылью, которая может быть получена во всех остальных случаях (табл. 8.6).

Статистик должен получить дополнительную информацию о состояниях природы при наблюдениях погоды в апреле, когда проводится посадка.

Таблица 8.6

 

Пусть X = { x₁, x₂ } - множество наблюдений, где х₁ и х₂ - наблюдается большое и малое количество осадков соответ­ственно.

В зависимости от состояния природы Q _j и наблюдения пого­ды х_i получим следующие значения условных распределений:

 

По двум решениям статистика а₁ и а₂ и результатам наблю­дения получаем четыре нерандомизированные функции решения d Î D (табл. 8.7).

Таблица 8.7

В статистической игре (W, D, R), которая посвящена выбору участков земли для посадки картофеля, определим функции риска R (Q, d):

 

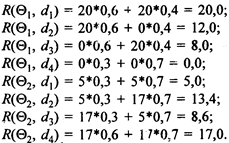
Полученные результаты функций риска R( Q, d) представим в табл. 8.8, откуда видно, что функция решения d₂ доминирует над функцией d₃. Следовательно, d₂ недопустима. Она не относится к подмножеству допустимых функций решения. Мы в этом убе­димся при расчете байесовских рисков.

Таблица 8.8

 

Будем считать, что в рассматриваемом районе априорное распределение состояний природы приводит к одинаковым шан­сам для сухого и влажного лета при исследовании состояний природы. Значит, Р( Q₁ ) = 0,5; P( Q₂ ) = 0,5.

Вычислим байесовский риск r (x, d):

 

Минимальный байесовский риск наблюдается для функции d₃, что не противоречит выводу, сделанному из табл. 8.8.

Вывод. Нерандомизированная функция решения d₃, кото­рая включает решение для d(x₁) = а₂ и d(x₂) = а₁, является бай­есовской функцией решения. Это оптимальная стратегия стати­стика: в рассматриваемых условиях, если весной много осадков (x₁), принимается решение а₂ о том, что картофель нужно сажать на сухих участках земли А₂. Если весной мало осадков (x₂), при­нимается решение а ₁ о посадке картофеля на участках А₁, где влажность почвы большая.

Задача 8.3. Планирование участков земли под посевы карто­феля методом линейного программирования. В задаче 8.2 мы получили оптимальное байесовское решение d₃. Теперь попро­буем получить минимаксную, более осторожную стратегию.

Минимаксную функцию решения следует искать как смешан­ную стратегию среди рандомизированных функций решения, по­тому что матрица значений функций риска R( Q, d) для нерандо­мизированных функций решения d Î D не имеет седловой точки.

Применяя метод линейного программирования и учитывая, что при оптимальном решении ограничения записываются как равенства, получаем из табл. 8.8 при ненулевых значениях h₁ и h₃ систему уравнений, которая включает цену игры v:

В результате решения этой системы уравнений получим:

Вывод. Минимаксная стратегия, еще более осторожная, чем оптимальная байесовская, для сельскохозяйственного предприя­тия заключается в использовании стратегий d₁ и d₃ с вероятно­стью соответственно 0,04 и 0,96.

Как это применять на практике?

Если весной наблюдается х₁ (большое количество осадков), то осуществляется случайный выбор с вероятностями 0,04 и 0,96 одного из решений: а₁ или а₂. При наблюдении х₂ (малое коли­чество осадков весной) принимается решение a₁ о посадке кар­тофеля на влажных участках А ₁.

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: