Макроэкономические решения

При применении теории статистических игр на предприятии, в фирме бывает возможным получить дополнительную статис­тическую информацию, которая позволяет перейти от стратеги­ческой к статистической игре с природой. Очень часто при воз­можности многократного повторения как состояний природы, так и решений статистика мы можем принимать минимаксные бай­есовские решения.

Для макроэкономических задач значительно реже удается получать информацию о состояниях природы. Кроме того, имея распределение вероятностей ее состояний, мы не всегда можем этой информацией воспользоваться. Принятие решения может носить одноразовый характер. В этой ситуации наилучшая бай­есовская стратегия при многократном принятии решения утра­чивает свои оптимизационные свойства.

Задачи, решаемые в условиях неопределенности, имеющие характер игры с природой, делятся на два типа:

1) в условиях полной неопределенности, когда отсутствует возможность получения дополнительной статистической инфор­мации о состояниях природы; основной моделью при этом слу­жит стратегическая игра (W, A, L), которая не преобразуется в статистическую;

2) в условиях риска, если существует возможность сбора до­полнительной статистической информации о распределении со­стояний природы; эти задачи можно преобразовать к статисти­ческой игре (W, D, R), в которой функции риска рассматривают­ся как платежи.

Рассмотрим практический пример.

Задача 6.3. Получение лицензии на новую продукцию.

Требуется выбрать лучшую лицензию на выпуск легкового автомобиля у иностранных фирм. Имеются четыре предложения, следовательно, множество решении А = {а₁, а₂, а₃, а₄}, где а₁ -решение о покупке лицензии у инофирмы A_i (i = ).

Фирмы требуют неодинаковые суммы за лицензии в зависи­мости от различных затрат на организацию производства и из­держек эксплуатации.

Известно, что основным требованиям владельцев автомоби­лей (эстетика, количество мест в салоне, скорость) удовлетворяют все четыре фирмы. В результате главным критерием являют­ся затраты, связанные со сделкой.

Пусть на основе экономического расчета вычислена эффек­тивность покупки каждой из четырех лицензий. Эта эффектив­ность зависит от длительности периода, в течение которого мож­но будет выпускать автомобили по лицензии, учитывая уровень их рентабельности и соответствия последним достижениям на­уки и техники в области автомобилестроения. Множество состо­яний природы , где Q₁, Q₂ - рентабельность и со­ответствие техническому уровню выпущенных по приобретен­ной лицензии первого и второго автомобилей, достигаемые со­ответственно через 15 и 25 лет.

Представим формулу экономической эффективности:

где У - продажная цена автомобиля;

С - себестоимость;

W- выигрыш игрока 1, в данном случае статистика, представляю­щего автомобильную промышленность.

Отразим в табл. 6.3 полученные значения эффективности W (Q, a).

Таблица 6.3.

О стратегиях природы нет информации, и ее невозможно получить.

Решение нужно найти при полной неопределенности, так как нет данных для перехода от стратегической игры к статистической.

Применим максиминный критерий Вальда.

Для этого перепишем табл. 6.3 и найдем минимальные зна­чения по строке и максимальные - по столбцу. Это определит матрицу игры (табл. 6.4).

Таблица 6.4

Матрица игры (W, A, W) имеет седловую точку, равную 22 %, поскольку

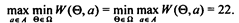
Итак, оптимальной нерандомизированной максиминной стра­тегией статистика (игрока 1), представляющего интересы авто­мобильной промышленности, будет решение а₂, что соответствует покупке лицензии у фирмы А₂ на производство легкового авто­мобиля.

Это наиболее осторожная стратегия в игре с природой при отсутствии дополнительной статистической информации. При этом в качестве функций платежей была принята эффективность сделки W (Q, a) = 22.