Проектирование маршрутов городского транспорта

Задача 8.1. Выбор трассы новой автобусной линии в городе. Построен за городом новый жилой микрорайон, который нужно связать с центром города. Имеем исходную стратегическую игру ( W ,A,L). Статистик пришел к выводу, что линию можно провести до пункта А₁, или А₂, или А₃. Решение А = {а₁, а₂, а₃}, где a₁, означает проведение трассы до А₁, а₂ - до А₂, а₃ - до А₃, причем А₁ и А₃ находятся в разных концах города. Множеством состоя­ний природы W являются Q₁, Q₂, Q₃ - состояния, когда большин­ство жителей микрорайона работает соответственно в окрестнос­ти пункта А₁, пункта А₂ и пункта А₃, находящегося в самом центре города.

Если принятое решение провести трассу не будет удовлетво­рять нужды жителей микрорайона, то транспортное предприя­тие понесет потери. Потери будут максимальными при ошибоч­ном решении проложить трассу к пункту А₃ вместо А₁ или на­оборот.

Решение. Функция L( Q, а) потерь характеризуется матри­цей (табл. 8.1).

Таблица 8.1

 

Преобразуем стратегическую игру (W, A, L) в статистичес­кую (W, D, R) при учете информации о действительном состоя­нии природы. Для этого проводится выборочный опрос жителей микрорайона. Результаты этого опроса образуют вектор

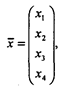
где x₁, х₂, х₃, - доля от общего числа опрошенных (не менее 50 %), которые предлагают строительство трассы до пунктов А₁, А₂, A₃ соответственно;

x ₄ — любое из трех направлений не получило решающего количества голосов.

Действительные данные результата опроса показали следую­щие вероятности рекомендаций жителей (табл. 8.2) в зависимо­сти от состояний природы Q.

Таблица 8.2

 

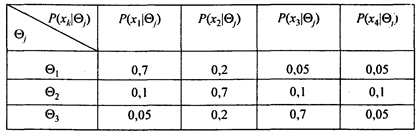
В результате опроса получаем условные вероятности P(x₁| Q₁ ) = P(x₂| Q₂ ) = P(x₃| Q₃ ) = 0,7. Пусть d(x) = а - нерандомизированная функция решения, преобразующая множество Х результатов эк­сперимента в множество решений. Множество D нерандомизи­рованных решений при наличии четырех результатов экспери­мента и трех возможных решений будет иметь 3⁴ = 81 различ­ную функцию решений статистика в статистической игре с при­родой (W, D, R}. Из них мы ограничимся шестью допустимыми функциями: d₁, d₂,..., d₆ (табл. 8.3).

Таблица 8.3

 

 

Какие же решения не вошли в допустимые? Недопустимые функции решения — это все функции d Î D, которые не ставят в соответствие хотя бы одному из результатов x₁, x₂, x₃ решение а₁, а₂, a₃ потому, что для этих функции значе­ние риска R( Q, d) будет всюду большим по сравнению с други­ми функциями решений. Результат х₄ при этом во внимание не принимается, поскольку он не отражает конструктивного пред­ложения.

Учтем полученные условные вероятности и, зная значения функций потерь, вычислим математические ожидания функций потерь, т. е. получим функции риска для допустимых функций решений:

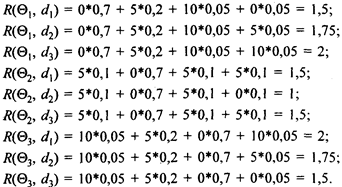
Из табл. 8.3 видно, что вне зависимости от х₁, х₂ х₃, х₄ реше­ние d ₄ будет соответствовать решению а₁, d₅ ® a₂, d₆ ® a₃.

Объединим все полученные решения в табл. 8.4 и выпишем минимальные значения функции риска по строке и максималь­ные значения - по столбцу.

Таблица 8.4

 

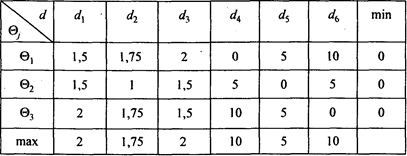
Таким образом, как показывает табл. 8.4, среди нерандо­мизированных функций решений нет минимаксной функции: v₁ =0< v ₂=1,75. Следовательно, минимаксную функцию реше­ния надо искать во множестве D* рандомизированных функций d.

В данной статистической игре (W, D, R) в качестве оптималь­ной нужно принять минимаксную функцию решения.

Для того чтобы найти рандомизированную минимаксную функцию решения d₀, следует обратиться к линейному програм­мированию (см. приложение).

Пусть d - распределение вероятностей на множестве неран­домизированных функций решения d. Обозначим это распреде­ление h₁ = P(d₁), h₂ = P(d₂),..., h₆ = P(d₆). Теперь обозначим через u цену расширенной статистической игры (W, D*, R) при рандо­мизации функций решений и запишем в терминах линейного про­граммирования задачу статистика, который решает ее в интере­сах транспортного предприятия.

Для этого воспользуемся данными табл. 8.4:

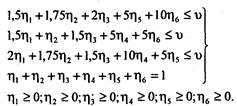
Преобразуем переменные, разделив h на цену игры u > 0, и введем дополнительные переменные q₇, q₈, q₉. В результате пе­рейдем от неравенств к равенствам:

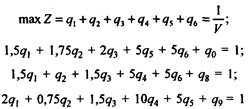
при q_j > 0, j = .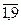

Решим эту задачу линейного программирования симплексным методом (техника решения известна и здесь не излагается) и получим базисное оптимальное решение:

q₁ = q₃ = 2/7; q₂ = q₄ = q ₅ = q _б = 0.

Значит, Z _max = q₁ + q₃ = 2/7 +2/7 = 4/7.

Отсюда u = l/Z_max = 2/7 = 1,75.

Перейдем к исходным переменным h_i = q_i u; i = 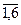, где h_i - вероятности, с которыми следует сочетать соответствующие нерандомизированные функции решения d_i (i = 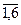). После пере­множения получим рандомизированные функции d:

Итак, получена минимаксная рандомизированная функция ре­шения d₀ с распределением вероятностей: P(d₁) = 1/2; P(d₃) = 1/2. Как ее охарактеризовать? Это смешанная стратегия d₀ с одина­ковыми вероятностями чистых функций решения d₁ и d₃. Они различаются только результатом статистического эксперимента.

Вывод. В задаче выбора транспортным предприятием наи­лучшей трассы маршрута новой автобусной линии получена оптимальная минимаксная функция решения:

• если по эксперименту с анкетами получен результат х ₁, или x₂, или x₃, то следует принять решение а ₁ или а₂, или a₃ соответ­ственно;

• если получен результат х₄, то нужно использовать механизм случайного выбора между решениями а₁ (трассу вести до А₁) и a₃ (трассу вести до А₃) с одинаковыми вероятностями, равными 0,5. Следует сделать одно важное замечание: в данном случае мы из расчетов получили одинаковые вероятности. (Это реше­ние не имеет ничего общего с принципом равновероятности, который иногда необоснованно применяется при отсутствии информации о возможных вероятностях событии.)

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: