Статистический контроль партии готовых изделий и вероятность перебоев производства

На основе статистических планов приемки продукции всегда должно быть известно, сколько изделий следует случайным об­разом отобрать для статистического контроля и при каких усло­виях принимается решение о браковке или приемке партии.

Планов контроля имеется большое множество, однако благо­даря своей простоте часто применяется одноступенчатый стати­стический план премки k|n, где п - объем выборки; k - приемоч­ное число. Если из проверенных изделий число дефектных Z не будет превышать k, партия принимается. Значит, k - допустимое число дефектных в выборке из п изделий.

Представитель торгового предприятия при Z £ k считает партию хорошей и принимает ее на основе анализа выборки. Затем производитель покрывает стоимость каждого обнаружен­ного в переданной партии бракованного изделия путем замены, бесплатного ремонта или другим путем, означенным в договоре.

Если Z > k, то партия не принимается торговым предприяти­ем, а производитель осуществляет сплошную проверку партии и выявляет дефектные изделия.

Задача 8.4. Выбрать оптимальное критическое число k. Зна­чение k может быть определено при помощи статистической игры.

Введем обозначения:

W (W ÎW), доля дефектных изделий, - состояние природы Q;

N - объем партии изделии;

W = [0,1] - интервал от 0 до 1 с включением границ этого интервала;

А = { а₁, a₂ } - множество решении статистика, где а₁, а₂ - ре­шения о приемке и о браковке партии со сплошным ее контро­лем соответственно;

С₁ - затраты на проверку одного изделия;

С ₂- сумма, уплачиваемая производителем за каждое обнару­женное дефектное изделие после приемки партии.

Функция потерь

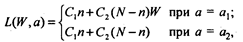
где С₁п - стоимость контроля выборочной совокупности изде­лии в процессе контроля;

C₂(N–n)W - сумма, выплачиваемая производителем за изделия, ког­да они окажутся дефектными после приемки;

С₁ n + С₂(N–п) - затраты на сплошной контроль, если партия не была принята.

Итак, стратегическая игра будет иметь вид (W, A, L). Для оп­ределенности будем считать:

• торговая фирма оплачивает только исправные изделия, а дефектные заменяются исправными;

• при большой партии распределение вероятностей случай­ной переменной - числа дефектных изделий Z - подчиняется биномиальному закону. Функция вероятности зависит от действи­тельной доли бракованных изделий в принимаемой партии W:

• контролер наблюдает число Z в выборке объема п;

• d(Z) = а - статистическая нерандомизированная функция решения контролера. Контролер может принять одно из двух зна­чений: a₁ (принять) или a₂ (не принять партию).

Однако нам необходимо осуществить оптимальный выбор критического числа k, поэтому перейдем к статистической игре. В этой игре используем информацию о числе Z забракованных изделий в выборке объемом п; распределение Z зависит от со­стояния природы W - доли дефектных изделий.

Решение. Для состояния природы W и статистической не­рандомизированной функции решения d(Z), определяющей кри­тическое число k при контроле партии готовых изделий, можно в статистической игре (W, D, R) найти функцию платежей или функцию риска R(W, d):

Это выражение можно раскрыть, используя биномиальное распределение.

Далее в качестве целевой функции d(Z), определяющей опти­мальное критическое число k выберем байесовскую нерандоми­зированную функцию. Пусть процесс производства является отлаженным, тогда доля дефектных изделий в партии W будет иметь бета-распределение, заданное на интервале [0,1]. В зави­симости от принятых параметров р и q можно определить апри­орное распределение доли дефектных изделий W в принимае­мых партиях.

Таким образом, априорным распределением x состояний природы W принимается бета-распределение с функцией плот­ности

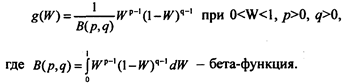
Известно, что существует связь между бета- и гамма-функ­циями:

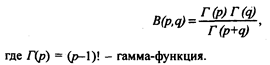
Байесовский риск при этом распределении будет

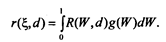
Этот байесовский риск следует минимизировать относитель­но k. При известных размерах партии N, выборки п, затрат C₁ и С₂, параметров априорного бета-распределения р и q байесовс­кий риск будет только функцией k:

r( x, d) = f(k).

Теперь нужно найти такое натуральное k, чтобы удовлетво­рялись неравенства

f(k) £ f(k+ 1) и f(k) £ f(k– 1)

Рассмотрим неравенство f(k) £ f(k+ 1), из которого следует, что f(k+ 1) – f(k) ³ 0.

Используя связи между бета- и гамма-распределениями 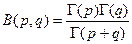и формулу гамма-функции Г(n) = (n– 1)!, где (n –1)! - факториал, получим f(k+ 1) – f(k) ³ 0, если С₂(р + k + 1 )/(р + q + п) – С₁ £ 0.

Значит, (p+k+ 1 ) ³ 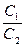(p+q+n) и неравенство f(k) £ f(k+ 1) выполняется при k ³ 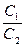(p+q+n) - (p+ 1).

Обратимся к неравенству f (k– 1 ) – f(k) ³ 0 и найдем значе­ние k, для которого оно выполняется. При этом необходимо пре­образовать байесовский риск r (x, d) = f(k), после чего получаем неравенство f (k– 1 ) – f(k) ³ 0, которое выполняется, если С₂ р + k)/(p + q + п) – C₁ £ 0. Тогда (p + k) £ 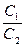(p+q+n), т. е. при k £ 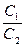(p+q+n) - p. В этом случае байесовский риск примет минимальное значение для такого натурального числа k, которое удовлетворяет двойному неравенству:

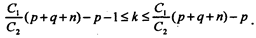
Вывод. С помощью нерандомизированной байесовской фун­кции получаем решение при одноступенчатом статистическом плане приемки партии изделий, если известно распределение доли дефектных изделий в партии, т.е. априорное распределение со­стояний природы.

Пример 8.1. Производитель продает торговой фирме боль­шую (п = 100) партию изделий. По договору представитель тор­говой фирмы отбирает случайным образом п = 30 изделий. Кон­троль проводится по согласованной программе при одноступен­чатом плане. Стоимость проверки одного изделия C₁ = 180 руб., стоимость исправного изделия С₂ = 2 000 руб.

Требуется найти критическое число k при предположении, что доля дефектных изделий W подчинена бета-распределению.

Предполагаем, что доля бракованных изделий при отлажен­ном производстве близка к нулю, поэтому g(W) будет иметь большое значение. Пусть аргументы бета-функции B(p,q) равны: p=1, q= 5.

Нужно построить график распределения и определить мини­мальное число k. (Функция на графике при росте доли дефект­ных изделий будет быстро стремиться к нулю.)

Решение. Определим B(p,q):

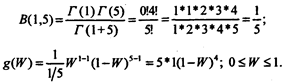
Используя значения доли W (пусть W = 0; 0,05; 0,1; 0,2;...,0,9;1), получаем:

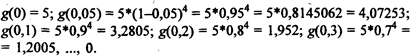
Составим таблицу распределения g{W) при значении аргумен­тов бета-функции: q = 5, р = 1 (табл. 8.9).

Таблица 8.9

 

Найдем критическое число k при п = 30, которое должно удовлетворять двойному неравенству:

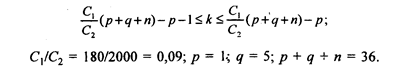
Подставив численные значения параметров в эти неравенства, получаем k:

0,09*36 - 1 - 1 £ k £ 0,09*36 - 1.

1,24 £ k £ 2,24.

Следовательно, k = 2.

Вывод. Критическое число равно 2, статистический план запишется (2|30).

Партия будет принята при числе бракованных в выборке из 30 изделий, не превышающем 2 шт. В противном случае партия будет забракована.

Пример 8.2. Для условий примера 8.1 при плане (2|30) под­считать функцию потерь при: k = 3; k = 2 и возможном отказе в принятой партии двух изделий из числа непроверенных (N-n), если N = 100; k = 2 и возможном возврате изделий из числа непроверенных, если W= 0,05.

Решение. Определим функцию потерь при k = 3, полагая согласно рис. 8.1, что р = 1:

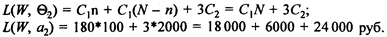
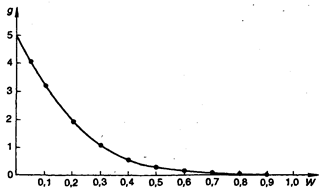
Рис. 8.1. Бета-распределение при р = 1,q=5

Найдем функцию потерь при k = 2, когда партия была при­нята, но затем в торговой фирме было обнаружено 2 неисправ­ных изделия из числа непроверенных при сдаче:

L(W, a₁) = 180 n +2C₂+2C₂ = 180*30 + 4*2 000 = 5 400 + 8 000 = 13400 руб.

Вычислим функцию потерь при k = 2 и возможных отказах при W =0,05:

L(W, а₁) = 180 n + 2 C₂ + C₂(N - n) = 5 400 + 4 000 + 70*0,050 C₂ = 9400 + 3,5*2000 = 16400 руб.

Поскольку 3,5 отказа невозможны (могут быть 3 или 4), до­бавляем (отнимаем) половину стоимости изделия и получаем:

L(W, a₁) = (16400 ± 1000) руб.

Пример 8.3. Оставим условия примера 8.1, но изменим объем выборки. Вместо п = 30 примем п = 45. Требуется определить критическое число k, если оно удовлетворяет двойному неравен­ству при нерандомизированной байесовской функции решения r( x, d)=f(k):

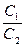(p+q+n) – p – 1 £ k £ 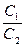(p+q+n) – p.

Решение. Запишем в принятых выше обозначениях усло­вия: С₁ = 180 руб.; С ₂ = 2 000 руб.; р = 1; q = 5, п = 45:

(p+q+n)=1+5+45=51; 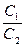= =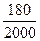0,09.

Вычислим минимальное значение k:

0,09*51 - 1 - 1 £ k £ 0,09*51 - 1;

2,59 £ k £ 3,59.

Таким образом, k = 3.

Вывод. Партия будет принята при k == 1, 2 или 3, а при k = 4 или более партия изделии будет забракована, 4 бракованных изделия будут заменены в выборке на годные, остальные 55 из 100 изделий будут проверены.

Пример 8.4. Оценить возможности сбоев производства из-за нарушения кооперированных поставок.

С помощью методов математического программирования можно составить оптимальный план производства. Однако этот план при нерегулярности кооперированных поставок смежников может быть фактически не реализован.

В данной ситуации возможно вычислить вероятность регу­лярности кооперированных поставок, что должно соответство­вать вероятности отсутствия сбоев производства.

Введем обозначения:

Q (состояние природы) - вероятность отсутствия сбоев про­изводства Q Î W = [0,1];

А = [0,1] - область решения статистика;

а - оценка вероятности Q.

Примем в виде квадратичной функцию потерь L( Q, a)= (Q - а)². Оценим вероятность Q по информации за предыдущий месяц. Пусть W и N - события, заключающиеся в том, что в предыду­щем месяце были соответственно выполнены и не выполнены кооперированные поставки. Пространство выборок Х= {W, N}; d - нерандомизированная функция решения статистика, отобра­жающая пространство выборок Х в пространство решений А.

Решение. Функция решения может быть записана следую­щим образом:

d(W) = a₁; d(N) = a₂; a₁ Î А; а₂ ÎА.

Имеет место статистическая игра (W, D, R).

Опишем функцию риска:

R( Q, d) = ML( Q, a).

Считаем, что вероятности событии будут:

P{W| Q } = Q; P{N| Q } = 1 - Q.

Запишем функцию риска через а и Q.

Предположим, что для ряда месяцев вероятность отсутствия сбоев кооперированных поставок - это случайная величина с бета-распределением, имеющим параметры р > 0 и q > 0.

Функция плотности распределения вероятностей будет иметь вид:

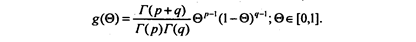
Вид данной функции плотности распределения вероятностей можно определить, если примем бета-распределение с парамет­рами р = 3 и q = 1 (рис. 8.2 и табл. 8.10).

Рис. 8.2. Бета-распределение при р = 3, q = 1

Таблица 8.10

 

Q		0,25	0,5	0,75
g( Q )		0,1875	0,75	1,6875

 

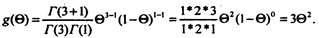
Бета-распределение является априорным распределением x состояний природы QÎW = [0,1]. Определим байесовский риск:

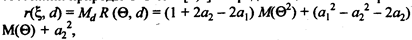
где M (Q) = m₁, и М (Q²) = т₂ - первый начальный и второй начальный момен­ты Q при бета-распределении с функцией плот­ности g( Q ) соответственно.

Известно, что

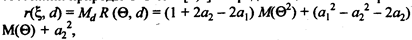
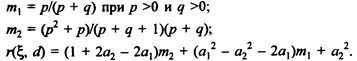
Чтобы определить выражения для получения a₁ и a₂, необхо­димо минимизировать байесовский риск для априорного распре­деления x. Продифференцируем r (x, d) по a₁ и a₂ и результаты приравняем к нулю:

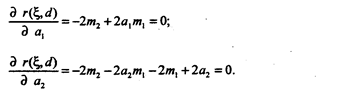
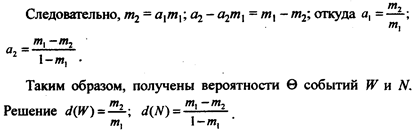
Вывод. Вероятность бесперебойной работы определится как т₂/т₁, если в прошлом месяце не было срывов кооперированных поставок. В противном случае вероятность бесперебойной рабо­ты предприятия будет равна (т₁ – m₂)/( 1 – m₁).

Пример 8.5. Оценить вероятность отсутствия перебоев в кооперированных поставках в данном месяце, если события W и N состоят соответственно в отсутствии и наличии срыва поста­вок в предыдущем месяце.

Априорное распределение - это бета-распределение с пара­метрами р = 3, q = 1. В данном распределении значения Q, близ­кие к единице, имеют большую плотность, чем значения, близ­кие к нулю.

Решение. Определим

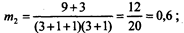
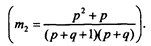
Вычислим

Определим вероятность бесперебойной работы предприятия при отсутствии срыва поставок в предыдущем месяце:

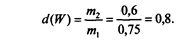
Оценим вероятность бесперебойной работы предприятия, если в прошлом месяце было событие N - срыв кооперированных поставок:

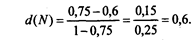
Выводы. Вероятность бесперебойной работы предприятия в данном месяце при условии выполнения договорных обяза­тельств по кооперированным поставкам, если в прошлом месяце также не было срывов, равна 0,8.

Если же в прошлом месяце был срыв в кооперированных поставках, то вероятность бесперебойной работы предприятия снизится в этом месяце до 0,6.

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: