Связь матричных игр с линейным программированием (основная теорема теории игр). Пример решения задачи

Первоначально развитие теории стратегических матричных игр осуществлялось параллельно и независимо от линейного программирования. Позже было установлено, что стратегичес­кая матричная игра может быть сведена к паре двойственных задач линейного программирования. Решив одну из них, полу­чаем оптимальные стратегии игрока 1; решив другую, получа­ем оптимальные стратегии игрока 2. Математическое соответ­ствие между стратегическими матричными играми и линейным программированием было установлено Дж. Б. Данцигом, сфор­мулировавшим и доказавшим в 1951 г. основную теорему тео­рии игр [23].

Теорема. Каждая матричная игра с нулевой суммой всегда имеет решение в смешанных стратегиях, т.е. существуют такое число v и такие стратегии U* и W* игроков 1 и 2 соответственно, что выполняются неравенства:

Поясним смысл доказываемых неравенств: если игрок 1 от­клоняется от своей оптимальной стратегии, то его выигрыш не увеличивается по сравнению с ценой игры; если от своей опти­мальной стратегии отклоняется игрок 2, то по сравнению с це­ной игры его проигрыш не уменьшается.

Доказательство. Пусть матрица игры равна A = 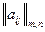. Всегда можно считать, что все коэффициенты а_ij > 0. Если это не так, то предположим, что наименьший из всех отрицательных коэффициентов есть а⁰ < 0. Тогда увеличим все элементы платежной матрицы на произвольное положительное число а > – а⁰. Функция выигрыша при этом окажется равной

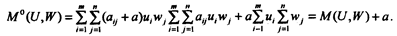
Из этого следует, что от увеличения всех элементов матрицы A = 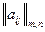на величину a цена игры увеличивается на эту величи­ну, причем оптимальные смешанные стратегии не изменяются.

Для определения среднего оптимального выигрыша игрока 1, соответствующего первоначальной платежной матрице, необхо­димо из найденной цены игры вычесть величину а.

Рассмотрим теперь пару двойственных задач линейного про­граммирования с матрицей условий A = 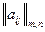(a_ij > 0), совпадаю­щей с платежной матрицей игры. Введем вектор ограничений прямой задачи В = (1, 1,..., 1) ^T, состоящий из т единиц (это вектор-столбец, для удобства записи представленный в виде транспонированной строки. Т - символ транспонирования мат­рицы), и вектор-строку коэффициентов линейной формы или функционала С = (1, 1,..., 1), состоящий из п элементов. Тогда в векторно-матричной форме соответствующая задача линей­ного программирования может быть записана следующим образом:

где Х- вектор искомых переменных задачи (П1). То же в скалярной форме:

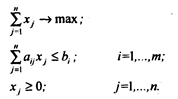
Двойственная задача к задаче линейного программирования (П1) может быть записана следующим образом:

где Y - вектор искомых переменных задачи (П2).

То же в скалярной форме:

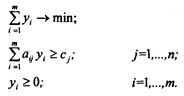
Все элементы матрицы А по предположению положительны, поэтому многогранные множества задач (П1) и (П2) ограниче­ны. Многогранник задачи (П1) не пуст, так как Х = 0 является допустимым планом. Следовательно, задача (П1), а с ней (по первой теореме двойственности) и задача (П2) разрешимы, и их функционалы в оптимальных планах совпадают (вторая теорема двойственности):

(С, X*) = (У* В).

С учетом выбранных единичных векторов С и В получаем следующее соотношение:

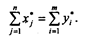
Из условия YA ³ С следует, что Y*¹ 0, поэтому

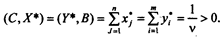
Положительность значения v обеспечивается положительно­стью всех значений элементов платежной матрицы А.

Обозначим U* = vY*, W* = vX*. Поскольку v, X*, Y* неотри­цательны, то U* ³ 0, W* ³ 0.

Кроме того, 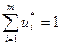, , 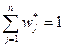так как по определению это частоты использования смешанных стратегии, а сумма частот равна единице. По условиям прямой и двойственной задач АХ £ В и YA ³ С. Оптимальные планы этих задач обозначим X* и Y *, причем по предположению X* = W*/v, Y*= U*/v. Поэтому

или

Умножим обе части неравенства (ПЗ) слева на произвольный w-мерный вектор U ³0, для которого справедливо

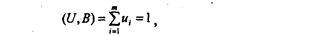
где В - единичный вектор.

Получим:

UAM* ³ v(U,B) = v,

т.е. имеет место неравенство

UAM* ³ v. (П5)

Также умножим обе части неравенства (П4) справа на произ­вольный n -мерный вектор W > 0, для которого справедливо

где С - единичный вектор.

Получим:

U * AM ³ v (C,W) = v,

т.е. справедливо неравенство

U*AM ³ v. (П6)

Сравнивая неравенства (П5) и (П6), приходим к соотноше­нию

UAW* £ v £ U*AW,

т.е. U* и W* - оптимальные стратегии, а v - цена игры с платеж­ной матрицей А, что и требовалось доказать.

Следствие (С1). В процессе доказательства основной теоре­мы теории игр с платежной матрицей A = 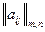(a_ij > 0) игре приведена в соответствие следующая пара задач линейного про­граммирования:

Составляющие оптимальных стратегий 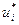и и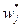гры связа­ны с компонентами и 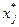оптимальных планов двойственных задач линейного программирования (П7) формулами:

Цена игры

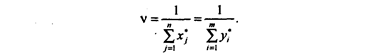
Следствие (С2). Вместо приведенной выше пары двойствен­ных задач линейного программирования (П7) иногда удобнее рассматривать другую пару задач, имеющих более ясный содер­жательный экономический смысл:

1. Прямая задача. Игрок 1 стремится увеличить цену игры:

v ® mах (П8)

при условиях:

т. е. игрок 1 действует так, чтобы его средний выигрыш при использовании его стратегий с частотами u_i для любой j -й стра­тегии игрока 2 был не меньше величины v, которую он стремит­ся увеличить;

т. е. сумма частот применения стратегий игрока 1 равна единице.

2. Двойственная задача. Игрок 2 стремится уменьшить свой проигрыш:

v ® min (П9)

при условиях:

т. е. игрок 2 действует так, чтобы его средний проигрыш при использовании его стратегий с частотами w_j для любой i -й стра­тегии игрока 1 не превышал величины v, которую он стремится уменьшить;

т. е. сумма частот применения стратегий игрока 2 равна единице.

В такой постановке каждая из задач (П8) и (П9) содержит на одно переменное (v) и на одно ограничение ( 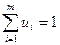или 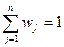) больше, т.е. размерности прямой и двойственной задач соответ­ственно увеличиваются, что может сыграть определенную роль при ручном решении задач линейного программирования, но не имеет практического значения при решении задач линейного про­граммирования на ЭВМ.

Пример решения задачи. Решить аналитически (используя мажорирование) игру с платежной матрицей

 

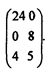
Решение. Если для первых двух строк матрицы взять ве­совые коэффициенты соответственно 0,25 и 0,75, то получим:

0,25 * 24 + 0,75 * 0 + 6 > 4;

0,25 * 0 + 0,75 * 8 = 6 > 4.

В итоге третья строка матрицы мажорируется выпуклой ли­нейной комбинацией первой и второй строк, поэтому третья строка вычеркивается, а матрица преобразуется к следующему виду:

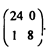
В матрице есть два нуля. Для того чтобы все элементы мат­рицы стали больше нуля, прибавим к каждому элементу по еди­нице. Матрица примет вид:

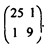
Далее ставим и решаем пару задач (двойственных) линейно­го программирования:

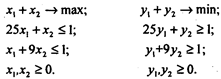
Для первой задачи (игрока 2) из условия угловой точки следует:

25 x₁ + x₂ = 1;

х₁ + 9 x₂ = 1,

откуда получаем оптимальное решение:

Находим оптимальные смешанные стратегии игрока 2:

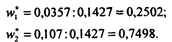
Для второй задачи (игрока 1) из условия угловой точки следует:

25 y₁ + y₂ = 1;

y₁ + 9 y₂ = 1,

откуда оптимальное решение равно:

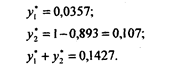
Оптимальными смешанными стратегиями игрока 1 будут:

Цена игры рассчитывается с учетом ее поправки на единицу:

v = 1:0,1427-1=6,008.

Ознакомившись теперь с основной теоремой теории игр, ме­тодом их сведения к паре двойственных задач линейного про­граммирования, мы видим, что, если в исходной матрице игры А в силу любых причин не произведены все возможные мажориро­вания строк и столбцов, это не скажется на результатах решения игры, но задачи линейного программирования получатся боль­шей размерности, чем потенциально они могли быть. Соответ­ственно в составе оптимальных смешанных стратегий игроков окажутся неактивные чистые стратегии.

КРАТКИЙ СЛОВАРЬ ТЕРМИНОВ

Вероятность случайного события - основная категория в тео­рии вероятностей - положительное число, заключенное меж­ду нулем и единицей: 0 < Р(А) < 1, где Р - обозначение ве­роятности, А - случайное событие.

Дискретные и непрерывные случайные величины - основ­ные числовые показатели в теории вероятностей. Дискретная случайная величина может принимать конечное или беско­нечное счетное множество значений. Возможные значения не­прерывной случайной величины занимают некоторый интер­вал числовой оси (конечный или бесконечный).

Дисперсия - числовая характеристика степени разброса значе­ний случайной величины. Дисперсия постоянной величины равна нулю. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D(CX) = C²D(X), где D - знак дисперсии; С — постоянная величина.

Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X + Y) = D (X) + D(Y).

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. Сумма посто­янной и случайной величин равна дисперсии случайной ве­личины. Дисперсия разности двух независимых величин рав­на сумме их дисперсий.

Достоверное событие - событие, в котором каждый элементар­ный исход испытания благоприятствует событию. Вероят­ность достоверного события равна 1.

Закон распределения случайной величины - соотношение, устанавливающее связь между возможными значениями слу­чайной величины и соответствующими им вероятностями. Простейшей формой задания закона распределения дискрет­ной случайной величины Х является таблица, в которой пе­речислены возможные значения случайной величины и со­ответствующие им вероятности (ряд распределения). Для не­прерывной случайной величины нельзя построить ряд распределения, так как она содержит бесконечное множество возможных значений, которые сплошь заполняют некоторый промежуток. Эти значения нельзя перечислить в какой-либо таблице. Каждое отдельное значение непрерывной случай­ной величины не обладает никакой отличной от нуля веро­ятностью.

Линейное программирование - раздел прикладной математи­ки, изучающий задачу отыскания минимума (максимума) ли­нейной функции многих переменных при линейных ограни­чениях в виде равенств или неравенств. Общую задачу ли­нейного программирования формулируют так:

найти минимум функции п переменных 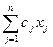при ограничениях:

Задача максимизации линейной функции сводится к задаче ее минимизации заменой знаков всех коэффициентов с_j на противоположные.

Математическое ожидание - числовая характеристика случай­ной величины, определяющая ее среднее значение. Свойства: математическое ожидание постоянной величины равно самой постоянной; постоянный множитель можно выносить за знак математического ожидания; математическое ожидание произ­ведения двух независимых случайных величин равно произ­ведению их математических ожиданий: M(ХY) = M(X)M(Y); математическое ожидание суммы (разности) двух случай­ных величин равно сумме математических ожиданий сла­гаемых: М(Х+ Y) = М(Х) + M(Y), где М - знак математи­ческого ожидания; М(Х) - математическое ожидание слу­чайной величины X.

Невозможное событие - событие, которое не может произойти в результате испытания. Вероятность невозможного события равна 0.

Независимое событие - событие В не зависит от А, если появ­ление события А не изменяет вероятность события В, т.е. условная вероятность события В равна его безусловной веро­ятности: Р_A(В) = Р(В). Если событие В не зависит от собы­тия А, то и событие А не зависит от события В. Это означает, что свойство независимости событий взаимно.

Попарно-независимые события - несколько событий, каждые два из которых независимы. Пусть А, В, С попарно независи­мы, тогда независимы А и В, А и С, В и С. Вероятность со­вместного появления нескольких событий, независимых в со­вокупности (АВС), равна произведению вероятностей этих событий: Р(АВС) = Р(А)Р(В)Р(С).

Практически достоверное событие - событие, вероятность которого не в точности равна единице, но очень близка к ней: Р(А)» 1.

Практически невозможное событие - событие, вероятность которого не в точности равна нулю, но очень близка к нему: Р(А)» 0.

Например, если парашют не раскрывается с вероятностью 0,01, - это недопустимо, а если поезд дальнего следования опоздает на 0,01 мин, можно считать, что поезд пришел вов­ремя.

Предмет теории вероятностей - изучение вероятностных зако­номерностей массовых однородных случайных событий.

Противоположное событие — событие А (не А), состоящее в непоявлении события А.

Теорема умножения вероятностей - инструмент для вычисле­ния вероятности совместного события: Р(АВ) = Р(А)Р_A(В), где Р(АВ) — вероятность совместного события; Р(А) - вероят­ность появления события А; Р_A(В) - вероятность появления события В при условии, что событие А уже наступило. Веро­ятность совместного появления нескольких событий равна произведению вероятностей одного из них на условные веро­ятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились. В частности, для трех событий: Р(АВС) = Р(А)Р_A(В) Р_AB(С). Порядок, в котором рас­положены события, может быть любым.

Теорема умножения независимых событий - частный случай теоремы умножения вероятностей. Вероятность совместного наступления независимых событий А и В равна произведе­нию вероятностей этих событий: Р(АВ) = Р(А)Р(В).

Функция распределения (или интегральный закон распределе­ния) - функция F(x), определяющая для каждого значения х вероятность того, что случайная величина Х примет значе­ние, меньшее х, т.е. F(x) = Р(Х < х). Эта функция распреде­ления существует как для дискретных, так и для непрерыв­ных случайных величин.

ЛИТЕРАТУРА

1. Вальд А. Последовательный анализ: Пер. с англ. - М.: Физмат-гиз, 1960.

2. Вентцель Е. С., Овчаров А. А. Теория вероятностей и ее инже­нерные приложения. - М.: Наука, 1988.

3. Гольштейн Е. Г., ЮдинД. Б. Новые направления в линейном про­граммировании. - М.: Сов. радио, 1966.

4. Дубров А. М. Последовательный анализ в статистической обра­ботке информации. - М.: Статистика, 1976.

5. Дубров А. М. Математико-статистическая оценка эффективности в экономических задачах. - М.: Финансы и статистика, 1982.

6. Дубров А. М. Статистические методы в инвестиционной дея­тельности // Рубин Ю. Б., Солдаткин В. И., Петраков Н. Я. Общая редакция. Инвестиционно-финансовый портфель. - М.: Совинтэк, 1993. - С. 163-176.

7. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математи­ческие методы в экономике. - М.: ДИС, 1997. - С. 245-267.

8. Клейнер Г. Б. Риски промышленных предприятий // Российский экономический журнал. - 1994. - № 5-6. - С. 85-92.

9. Клейнер Г. Б., Тамбовцев В. Л., Качалов Р. М. Предприятие в нестабильной экономической среде: риски, стратегии, безопасность. -М.: Экономика, 1997.

10. Комарова Н. В., Гаврилова Л. В. Фирма: стратегия и тактика управления рисками // Вестник Санкт-Петербургского университета. Сер. 5. Экономика. - 1993. - Вып. 2 (12). - С. 92-95.

11. Лагоша Б. А. Об оценке эффективности инвестиционных про­ектов //Тез. докл. научной конференции «Организационные науки и про­блемы государственного регулирования рыночной экономики». - М.:

ЦЭМИ РАН, Международная академия организационных наук, 1996. -С. 75-77.

12. Мак Кинси Дж. Введение в теорию игр: Пер. с англ. - М.: Физматгиз, 1960.

13. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение: Пер. с англ. - М.: Наука, 1970.

14. Основные методические положения оптимизации развития и размещения производства / Под. ред. академиков А. Г. Аганбегяна и Н. П. Федоренко. - М.: Наука, 1978.

15. Ожегов С. И. Словарь русского языка. - М.: Русский язык, 1981.

16. Первозванский А. А., Первозванская Т.Н. Финансовый рынок: расчет и риск. - М.: Инфра-М, 1992.

17. Самуэльсон П. Экономика. Т. 1. - М.: МГП «Алгон», ВНИИСИ, 1992.

18. Соколинская Н. Э. Экономический риск в деятельности коммер­ческого банка. (Методы оценки и практика регулирования). - М.: Об­щество «Знание» РСФСР, 1991.

19. Уилкс С. Математическая статистика. - М.: Наука, 1967.

20. Хозяйственный риск и методы его измерения: Пер. с венг. / Т. Бочкаи, Д. Месена, Д. Мико, Е. Сеп, Э. Хусти. — М.: Экономика, 1979.

21. Gren J. Ocena jacosej wyrobow obiektow ze wzgledn na wielle wymagan. - Warszawa, 1970.

22. Gren J. Statystyczne i ich Zastosowania. Panstwowe Wydawnictwo Ekonomiczne. - Warszawa, 1972.

23. Dantzig G. B. A proof of the equivalence of the programming and the game problem. Activity Analysis of Production and Allocation, ed. By Koopmans T. C., Cowles Commission Monograph, № 13, New York, Wiley, 1951. -P.330-335.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

Безразличие к риску 73, 74

Безусловный денежный" эквива­лент (БДЭ) 50, 67

Величина страхования оптималь­ная 78, 80

Вероятность 13, 15, 25, 33, 57, 62, 65, 72, 81, 101, 112, 117, 157

Дерево решений 47, 48, 53

Дисперсия 13, 58

Задача линейного программиро­вания 19, 30, 36, 86, 90,158, 162

Игра антагонистическая 18, 108, 113

одношаговая 19

многошаговая 19

с природой 20, 38, 45, 64

с седловой точкой 22, 24, 26, 33, 37

статистическая 20, 108, 110, 111, 114, 123, 129, 136, 149, 153

стратегическая 16, 20, 38, 42, 113, 114, 123, 129, 153

Инвестиции 86, 88, 92, 99, 104

Индекс риска 86

Комбинация стратегий линейная выпуклая 33, 34

Коэффициент дисконтирования 93, 94, 97, 99, 103, 106

Критерий максимакса 42, 45

минимаксного риска (Сэвиджа) 43, 45

пессимизма-оптимизма (Гурвица) 43, 44, 45

Мажорирование (доминирова­ние) стратегий 32, 35, 39, 41, 164

Максимин 21, 22

Математическое ожидание 13, 26, 58, 101, 111, 113

Матрица выигрышей 41, 43, 47

платежная 17, 29, 32, 38, 40, 47, 51, 56, 60, 64

рисков 40, 43, 47

Минимакс 21, 22

Неопределенность 40, 42

Несклонность к риску 73, 74

Ожидаемая денежная оценка (ОДО)50, 52, 55,65, 67, 71, 74, 77

Полезность по Нейману - Моргенштерну 70, 71, 73, 76, 80

Планирование финансовое 86

Рандомизация 109, 112

Риск 10, 38, 40, 46, 59, 68, 71, 74, 76, 89, 109, 114, 115

Склонность к риску 44, 59, 73, 74, 76

Спрос на страхование 80, 82

Среднее квадратичное отклоне­ние 13, 59, 61

Стратегия активная 27, 29

игрока 17, 20, 158

оптимальная 24, 27, 29, 108

смешанная оптимальная 26, 27, 29, 30

чистая оптимальная 23

Стоимость проекта чистая при­веденная 93, 96, 97,99

Теорема основная теории игр 158, 165

Теория игр 16

статистических решений 46

Точка седловая 20, 23

Функция рандомизированная 110, 136, 141

нерандомизированная 110, 124, 136, 140, 144, 149

потерь 111

решения байесовская 112, 114

риска 111, 112, 141

Цена игры 22, 26, 27, 29

чистая верхняя 21, 24

чистая нижняя 21, 24

Ценность ожидаемая точной информа­ции 55, 56

фирмы 96

 

Учебное пособие

Дубров Абрам Моисеевич

Лагоша Борис Александрович

Хрусталев Евгений Юрьевич

МОДЕЛИРОВАНИЕ РИСКОВЫХ СИТУАЦИЙ В ЭКОНОМИКЕ И БИЗНЕСЕ

Ведущий редактор Л.А. Табакова

Редактор А.М. Мжтормка

Художественный редактор Ю.И. Артюхов

Технический редактор Е.В. Кузьмина

Корректоры Т.М. Колоакова, Т.М. Васильева

Обложка художника Н.М. Биксеитеевж

Компьютерная верстка О.Е. Хрусталева

ИБ№3965

Лицензия ЛР № 010156 от 29.01.97

Подписано в печать 17.01.2000. Формат 60х88/16

Гарнитура «Таймс». Печать офсетная

усл.п.л. 10,8. Уч.-изд. л. 8.23

Тираж 4000экз. Заказ 325 «С» 031

Издательство «Финансы и статистика»

101000, Москва, ул. Покровка, 7

Телефон (095) 925-35-02, факс (095) 925-09-57

E-mail: mail@finstat.ru http://www. finstat.ru

Великолукская городская типография

Комитета по средствам массовой информации и связям

с общественностью администрации Псковской области,

182100, г. Великие Луки, ул. Полиграфистов, 78/12

Тел./факс: (811-53) 3-62-95

E-mail: VTL@MART.RU

 

⇐ Предыдущая16171819202122232425

Поделиться:

Воспользуйтесь поиском по сайту: