Прямая в плоскости. Прямая будет принадлежать пло­скости и в том случае, если она будет проходить через одну точ­ку этой плоскости параллельно ка­кой-либо прямой, лежащей в этой плоскости.

Прямая в плоскости

Из элемен­тарной геометрии известно, что пря­мая принадлежит плоскости, если две ее точки принадлежат пло­скости.

Прямая будет принадлежать пло­скости и в том случае, если она будет проходить через одну точ­ку этой плоскости параллельно ка­кой-либо прямой, лежащей в этой плоскости.

Любая прямая АВ, АС, ... принад­лежит плоскости, заданной треуголь­ником ABC, так как имеет с ней це­лый ряд общих точек, в том числе точки А и В, А и С и т. д.

Плоскость задана парал­лельными прямыми АВ и CD (рис. 3).

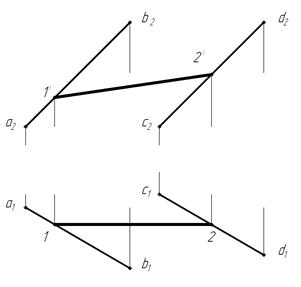
Рис. 3

Тре­буется построить фронтальную проекцию прямой, лежащей в этой пло­скости, если задана ее горизонтальная про­екция.

Найдем при помощи линий связи фрон­тальные проекции 1' и 2' точек 1 и 2, ко­торые являются точками пересечения задан­ных прямых с прямой 12 и, следователь­но, лежат в плоскости, определяемой параллельными прямыми. Эти проекции бу­дут лежать на фронтальных проекциях а₂ в₂ и c₂d₂ прямых. Через точки 1' 2' проводим фронтальную проекцию прямой 12.

Точка в плоскости

Точка принад­лежит плоскости, если она принад­лежит прямой, принадлежащей этой плоскости. Например, точки А, В, С, ... принадлежат плоскости, задан­ной треугольником ABC (рис. 4), так как точка А лежит на прямой АВ (а₁ 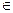a₁b₁, а₂ 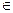a₂b₂), точка В — на прямой ВС (b₁ 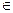b₁c₁, b₂ 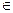b₂c₂) и т. д., которые в свою очередь относятся к заданной плоскости.

Пример. В плоскости, заданной тре­угольником ABC, построить точку D (рис. 4).

Рис. 4

 

Проведем в треугольнике любую пря­мую, например С1(с₁1, с₂1'), и возьмем на ней точку D(d₁, d₂). Проекции точки должны при­надлежать одноименным проекциям прямой (т. е. d₁ c₁1, d ₂ c₂1'). Точку D можно было бы отметить и на любой имеющейся в пло­скости прямой, например на прямой АВ, АС и т. д.

Главные линии плоскости

Некоторые прямые, лежащие в плоскос­ти, могут занимать в ней особое по­ложение, например, быть параллель­ными плоскостям проекций ( т. е. быть прямыми уровня ). Такие прямые называют главными линиями плоскости.   

К ним относятся:

1) горизонталь — прямая, ле­жащая в данной плоскости и парал­лельная горизонтальной плоскости проекций (прямая G (g₁, g₂) на рис. 5);

2) фронталь — прямая, лежа­щая в плоскости и параллельная фронтальной плоскости проекций (прямая F (f₁, f₂) на рис. 5);

3) профильная линия — прямая, лежащая в плоскости и па­раллельная профильной плоскости проекций (прямая I (i₁, i₂) на рис. 5).

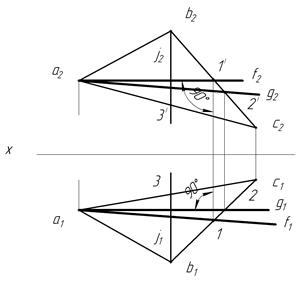
Рис. 5

Так как горизонталь плоскости па­раллельна горизонтальной плоско­сти проекций, то ее фронтальная про­екция на чертеже параллельна оси х. У фронтали горизонтальная про­екция параллельна оси х.

ПОСТРОЕНИЕ НА ЧЕРТЕЖЕ ИСТИННОЙ ВЕЛИЧИНЫ

 ОТРЕЗКА ПРЯМОЙ СПОСОБОМ  ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

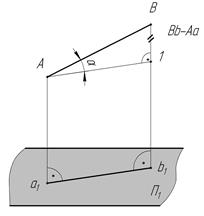
Ранее было показано, что отрез­ки прямых общего положения ни на одну из плоскостей не проецируются в истинную величину. Однако в ряде задач возникает необходимость оп­ределить по чертежу длину отрезка прямой общего положения или по­строить углы наклона прямой к плос­костям проекций. В этом слу­чае используют способ построения прямоугольного треугольника.

Истинная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом кото­рого является проекция отрезка на одну из плоскостей проекций, а дру­гим — разность расстояний концов отрезка от этой же плоскости.

                                                                        

                                                                          

                        

 

 

  а)                                                                                 б)                       

Рис. 6

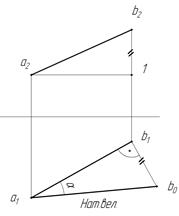
Из рисунка 6, а, на котором показано проеци­рование отрезка АВ на плоскость П₁, следует, что истинная величина от­резка АВ будет являться гипотену­зой прямоугольного треугольника AB1, в котором один катет равен про­екции отрезка (A1 = a ₁b ₁) по построе­нию, а другой — разности расстоя­ний концов отрезка от плоскости проекций.

На чертеже эти построения выпол­няют так. Одну из проекций отрез­ка, например горизонтальную a₁b₁ (рис. 6, б), берут в качестве одного из катетов прямоугольного треуголь­ника, второй катет принимают рав­ным разности расстояний точек А и В (рис. 6 а) от плоскости проекций П₁. Для отыскания этой разницы на чертеже через точку а₂ проводят вспомогательную прямую, перпен­дикулярную к линии связи b_1, b₂. От­резок b₂1 — искомый второй катет. Выполнив необходимые построения, найдем истинную величину отрезка АВ (на чертеже она равна a₁b₀).

По рис. 6а видно, что угол на­клона прямой линии к плоскости проекций определяется как угол, со­ставленный прямой с ее проекцией на эту плоскость. Этот угол (рис. 6а) входит и в прямоугольный тре­угольник, который строят для опре­деления истинной величины отрезка. Поэтому на рис. 6б угол с верши­ной в точке а₁, т. е. угол 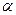, будет ра­вен углу наклона прямой АВ к го­ризонтальной плоскости проекций П₁.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: