Проекции пирамид. Проекции цилиндров

ПРОЕКЦИИ ПИРАМИД

Построение проекций треугольной пирамиды начинается с построения основания, горизонталь­ная проекция которого представляет собой тре­угольник без искажения (рис. 36, а). Фронталь­ная проекция основания — отрезок горизонталь­ной прямой.

 

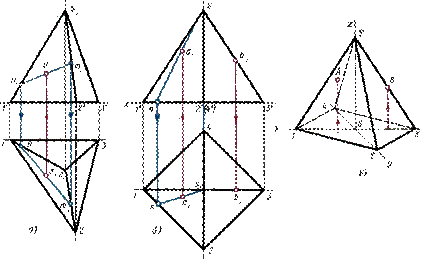
Рис. 36

 

Из горизонтальной проекции точки s₁ (верши­ны, пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s₂ вершины. Соединяя точку s₂ с точками 1', 2' и 3', получают фронтальные проекции ребер пира­миды.

Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки s₁ с горизонтальными проекциями точек 1, 2 и 3.

Пусть, например, дана фронтальная проекция а₂ точки А, расположенной на грани пирамиды 1s₁2, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а₂ произвольную вспомогательную прямую и продолжим ее до пересечения с фронтальными проекциями 1's₂ и 2' s₂ ребер в точках n₂ и m₂. Затем проведем из точек n₂ и m₂ линии связи до пересечения с горизонтальными проекциями 1s₁ и 2s₁ этих ребер в точках n₁ и m₁. Соединив n₁cm₁, получим горизонтальную проекцию вспомогатель­ной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию а₁ точки А. Профильную проекцию этой точки нахо­дят по линиям связи.

Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на рис. 36, б.  Дана четырехугольная правильная пирамида. Через заданную фронтальную проек­цию а₁ точки А проводят вспомогательную пря­мую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию n₁s₁ вспомогательной прямой находят с помощью линии связи. Искомая горизонтальная проекция а₁ точки А находится на пересечении линии связи, проведенной из точки а₂, с горизон­тальной проекцией n₁s₁ вспомогательной прямой.

Фронтальная диметрическая проекция рассмат­риваемой пирамиды выполняется следующим образом (рис. 36, в).

Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — половину длины диагонали 24. Из точки О пере­сечения диагоналей проводят ось z и на ней от­кладывают высоту пирамиды. Вершину S соединя­ют с вершинами основания прямыми линиями - ребрами.

Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чер­тежа. От начала координат О по оси х отклады­вают координату х_А, из ее конца параллельно оси у — половину координаты у_А и из конца этой ко­ординаты параллельно оси z — третью координату z_A. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х от­кладывают координату х_в и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.

 

ПРОЕКЦИИ ЦИЛИНДРОВ

Боковая поверхность прямого кругового цилин­дра получается вращением отрезка АВ образую­щей вокруг оси, параллельной этому отрезку. На рис. 37, а представлена изометрическая проекция цилиндра.

Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 37, б и в.

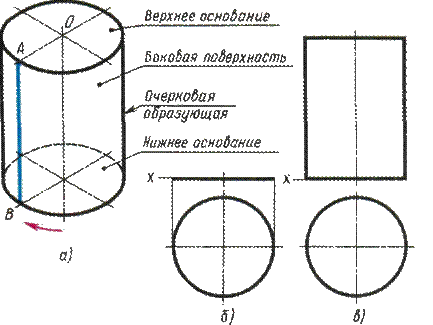
Рис. 37

Построение начинают с изображения основания цилиндра, т. е. двух проекций окружности (рис. 37, б). Так как окружность расположена на плоскости П₁, то она проецируется на эту плос­кость без искажения. Фронтальная проекция ок­ружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окруж­ности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайние) обра­зующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, кото­рый является фронтальной проекцией верхнего основания цилиндра (рис. 37, б).

Определение недостающих проекций точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном слу­чае затруднений не вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 38, а).

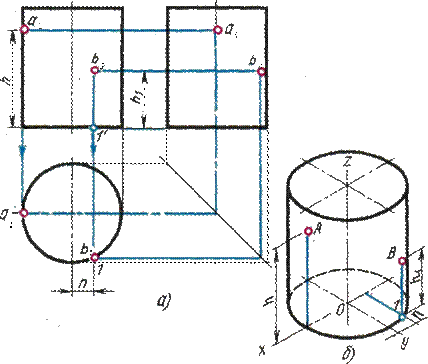
Рис. 38

Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а₂ и b₂ вертикальные линии связи до их пересечения с окружностью в искомых точ­ках а₁ и b₁.

Профильные проекции точек А и В строят так­же с помощью вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчи­вают, как показано на рис. 38, б.

В изометрии точки А и В строят по координа­там. Например, для построения точки В от начала координат О по оси х откладывают координату х_в = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси z проводят прямую, на которой откладывают координату z_B = h₁ точки В.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: