Изображение взаимно перпендикулярных плоскостей

ИЗОБРАЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ

Две плоскости Р и Q перпендику­лярны, если одна из них (Р) прохо­дит через перпендикуляр АВ к другой либо перпендикулярна к прямой CD, принадлежащей ей (т. е. плос­кости Q на рис. 18).

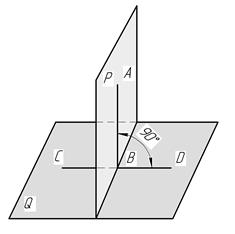
Рис. 18

 Следователь­но, чтобы построить плоскость, пер­пендикулярную к заданной, нужно либовосстановить к данной плоскости перпендикуляр и через него провес­ти новую плоскость, либо провести в заданной плоскости прямую и пер­пендикулярно к ней взять искомую плоскость. Таким образом, построе­ние взаимно перпендикулярных плос­костей сводится к построению вза­имно перпендикулярных прямой и плоскости.

На рис. 19 показана плоскость P(DE 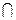L), перпендикулярная к плоскости, заданной треугольником ABC, проходящая через данную пря­мую DE.

 

Рис. 19

 

Для построения искомой плоско­сти Р, в плоскости, заданной тре­угольником ABC, построены сначала горизонталь A1 и фронталь А2, за­тем через произвольную точку пря­мой DE (например, точку D)проведена прямая L так, что ее горизон­тальная проекция l₁ перпендикуляр­на к горизонтальной проекции a₁1 го­ризонтали A1, а фронтальная l₂ — к фронтальной проекции а₂ 2'  фронтали А2 этой плоскости. Пересека­ющиеся прямые DE и вновь постро­енная L определяют искомую плос­кость Р, перпендикулярную к плос­кости, заданной треугольником ABC.

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1(лист 2)

Выполнить графическую работу на формате А3 по представленному образцу на рис. 20. Варианты заданий взять из таблицы 4.

 

Даны плоскость треугольника АВС и точка D.

 

1. Определить расстояние от точки D до плоскости АВС;

2. Построить плоскость, параллельную плоскости АВС, и отстоящую от нее на расстоянии 35 мм;

       

Таблица 4

 

№ варианта

А

В

С

D

x

y

z

x

y

z

x

y

z

x

y

z

 

Рис. 20

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Суть способа замены плоскостей проекций как способа преобразова­ния чертежа состоит в переходе от данной системы плоскостей проек­ций к новой. При этом отрезки пря­мых и плоские фигуры в процессе преобразования остаются на месте, а их новые проекции получаются за счет введения дополнитель­ных плоскостей проекций.

Пусть в системе плоскостей проек­ций задан отрезок АВ (рис. 21), не параллельный ни одной из плос­костей проекций. Определим по черте­жу его длину, т. е. истинную величину.

 

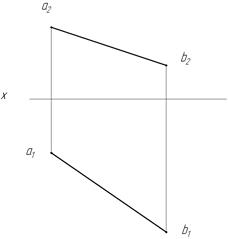
Рис. 21

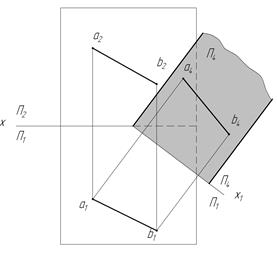
Для этой цели необходимо выпол­нить следующие преобразования: взять новую плоскость П₄, параллель­ную отрезку АВ, и построить на ней проекцию а₄b₄ (рис. 22, а).

 

     а)                                                                     б)

 

            а)                                                                   б)

Рис. 22

На плоскость П₄ отрезок АВ прое­цируется в истинную величину а₄b₄  Расстояние новой плоскости проек­ций П₄ от отрезка АВ произвольное.

Таким образом, выполняя указан­ные преобразования, мы заменили фронтальную плоскость проекций П₂  другой П₄, т. е. заменили одну  систему плоскостей проекции 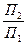другой 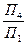. Новая плоскость проекций должна быть обязательно перпендикулярна к одной из основных плоскостей проекций, в данном случае   П₁ (П₄  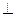П₁), т. е. той плоскости ста­рой системы, которая является общей для двух систем плоскостей проек­ций. Для получения нового чертежа (рис. 22, б) плоскость П₄ поворачи­вают вокруг линии пересечения плоскостей (оси х₁) до совмещения с плоскостью П₁.

Как выполняют такое преобразо­вание на чертеже?

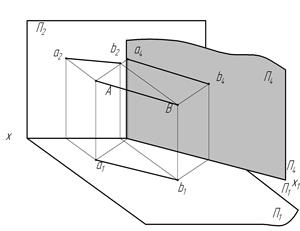
Из рис. 22, а видно, что новая ось проекций (мы ее обозначили х₁) располагается параллельно горизон­тальной проекции a₁b₁ отрезка. По­этому на чертеже необходимо внача­ле взять на произвольном расстоя­нии новую ось проекций х₁, парал­лельную отрезку a₁b₁, провести из то­чек а₁ и b₁ перпендикулярно к оси х₁ линии связи и на них от оси х₁ отло­жить высоту точек А и В, взяв их с фронтальной проекции (рис. 22, б). При проецировании отрезка АВ на плоскость П₄  высота точек  А и В остается прежней. На чертеже (рис. 23) соответствующие высоты отмечены дугой. Полученные точки соединяют прямой линией. Отрезок а₄b₄  определяет длину от­резка АВ (рис. 22, б).

 

                                                                

 

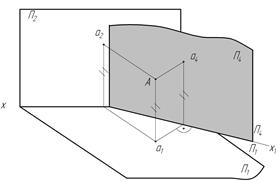              Рис. 23                                   Рис. 24

На рис. 23 показана последова­тельность построения чертежа точки А в новой системе плоскостей проекций.  Построения по наглядному изображению показано на (рис. 24).

 

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: