Применение способов. Преобразования чертежа к решению.  метрических задач

ПРИМЕНЕНИЕ СПОСОБОВ

ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА К РЕШЕНИЮ

 МЕТРИЧЕСКИХ ЗАДАЧ

В процессе изложения сущности способов преобразования чертежа мы рассмотрим несколько приме­ров решения метрических задач с применением этих способов. В част­ности, задачи на построение величин отрезков пря­мых и плоских фигур.

Рассмотрим дополнительно неко­торые метрические задачи, связан­ные с определением расстояний и углов.

1. Необхо­димо определить истинную ве­личину треугольника ABC, являющегося плоскостью общего положения (рис. 25).

 

 

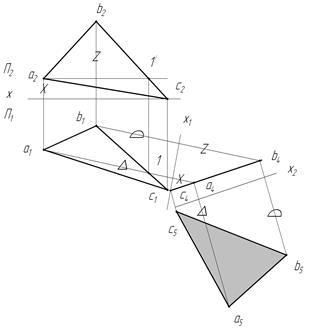
Рис. 25

В этом случае нужно последователь­но заменить две плоскости проекций, так как замена одной основной пло­скости проекций не позволяет приве­сти фигуру в требуемое частное по­ложение.

Сначала заменяем, например, плоскость проекций П₂ плоскостью П₄. Плоскость П₄  располагаем так, что­бы фигура, величину которой опре­деляем, стала в новой системе вна­чале проецирующей. Значит, пло­скость П₄  должна быть перпендику­лярна к плоскости треугольника ABC. С этой целью в треугольнике ABC проведена горизонталь а₁1. Перпендикулярно к ее горизонталь­ной проекции а₁1 на чертеже прове­дена новая ось проекции х_1.

На плоскости П₄ высоты точек А, В, С найдены по фронтальной про­екции. На эту плоскость проекций П₄ треугольник ABC спроецировался в линию b₄a₄c₄.

Затем параллельно треугольнику ABC располагают новую плоскость П₅ (на чертеже ось х₂ проведена па­раллельно проекции b₄a₄c₄ тре­угольника ABC) и выполняют по­строения. Расстоя­ния от оси х₂ до вершин треугольни­ка а₅b₅c₅ на плоскости  П₅ равны рас­стоянию от точек a₁b₁c₁ до оси х₂. На чертеже они помечены специальны­ми значками.

Таким образом, только при помо­щи последовательной замены обеих плоскостей проекций на новые мож­но произвольную плоскость сделать плоскостью уровня.

 2. Необходимо определить угол между двумя пло­скостями. Две плоскости, пере­секаясь между собой, образуют че­тыре попарно равных двугранных угла. Каждый из них измеряется линейным углом, который получает­ся при пересечении этих плоскостей третьей плоскостью, перпендикуляр­ной к линии их пересечения. Истин­ную величину этого угла можно оп­ределить несколькими способами. Наиболее простой из них — способ замены плоскостей проекций. Суть решения задачи состоит в том, что проекцию ребра двугранного угла двойной заменой преобразуют в точ­ку, а проекции граней — в две пере­секающиеся прямые. Угол между этими прямыми и будет искомым (рис. 26).

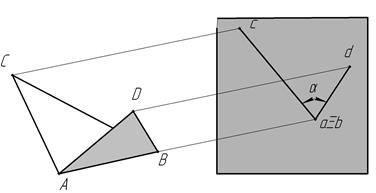
Рис. 26

Решение задачи на чертеже вы­глядит следующим образом. Первый раз новую плоскость проекций вы­бирают параллельно ребру АВ, вто­рой— перпендикулярно к нему. На рис. 27 угол  представляет собой проекцию двугранного угла и выра­жает его величину.

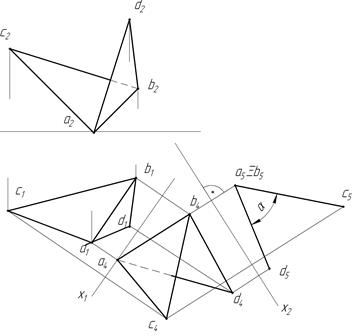
Рис. 27

3. Расстояние от точки до плоскости. Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из дан­ной точки на плоскость. Для реше­ния задачи необходимо так преоб­разовать чертеж, чтобы плоскость в новом положении стала проецирую­щей. На рис. 28 показано решение задачи путем применения способа замены плоскостей проекций.

 

 

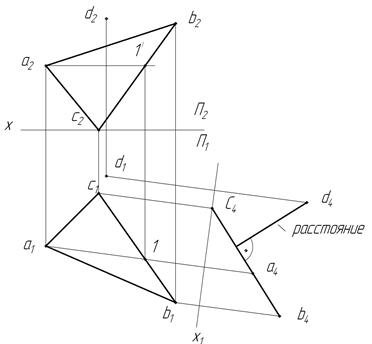
Рис. 28

4. Расстояние между дву­мя скрещивающимися пря­мыми. Если обе заданные в усло­вии прямые являются прямыми об­щего положения, то решение задачи сводится к такому преобразованию чертежа, в результате которого про­екция одной из данных прямых спроецируется в точку. Это построе­ние можно выполнить двойной заме­ной плоскостей проекций (рис. 29).

Первую новую плоскость проекций П₄ выбирают параллельно одной из данных прямых, например прямой АВ, вторую плоскость П₅ — перпен­дикулярно к этой прямой. Затем из точки b₅, 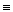а₅, в которую спроецировалась прямая АВ на плоскость П₅, нужно опустить перпендикуляр на c₅d₅ — проекцию прямой CD на пло­скость П₅. Полученная прямая k₅a₅ b₅  e₅ есть искомое расстоя­ние.

 

 

Рис. 29

На чертеже (рис. 29) отрезок ЕК изображен на всех дополнительных и основных плоскостях проекций.

 

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: