Построение точки пересечения пря­мой

ПОСТРОЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯ­МОЙ

ОБЩЕГО ПОЛОЖЕНИЯ С ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ

Для построе­ния точки пересечения прямой с плоскостью общего положе­ния необходимо:

 1) провести че­рез данную прямую вспомогатель­ную плоскость;

 2) построить линию пересечения вспомогательной плос­кости с заданной;

 3) найти точку пересечения построенной прямой с заданной, которая и будет искомой.

В качестве вспомогательной  необ­ходимо выбирать проецирующую плоскость. Тогда данную задачу можно свести к предыдущей задаче на пересечение двух плоскостей, из которых одна проецирующая.

Пусть необходимо построить точ­ку пересечения прямой L с плос­костью, заданной параллелограммом ABCD (рис. 10).

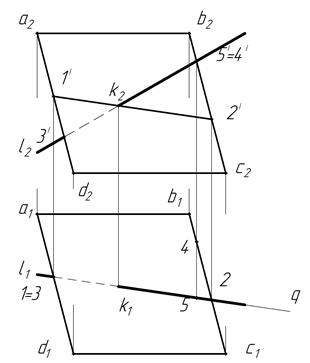
Рис. 10

Проведем через заданную прямую вспомогательную плоскость, напри­мер горизонтально-проецирующую Q. Горизонтальная проекция q этой плоскости и горизонтальная проек­ция l прямой совпадут. Затем построим линию пересечения плоскости Q с плоскостью, заданной четырехугольником ABCD. Посколь­ку выбранная вспомогательная плос­кость Q проецирующая, то горизон­тальная ее проекция совпадает с проекцией прямой l₁. Обозначим горизонталь­ные проекции 1, 2 и найдем с помощью линий связи их фрон­тальные проекции 1', 2' (рис. 10). Точка 1 принадлежит прямой a₁d₁, поэтому ее фронтальная проекция 1' лежит на фронтальной проекции a₂d₂ прямой. Точка 2 принадлежит прямой b₁ с₁, ее фронтальная проек­ция 2' лежит на фронтальной проек­ции b₂с₂. Соединив фрон­тальные проекции 1' и 2', получим фронтальную проекцию линии пересечения заданной и вспомогательной плоскостей. Она пересекается с фронтальной проек­цией l₂ в точке k₂, которая и будет фронтальной проекцией точ­ки пересечения прямой L с плос­костью ABCD.

Горизонтальную проекцию k₁ точ­ки К найдем на горизонтальной про­екции l₁ прямой L, проведя линию связи из k₂ до пересечения с прямой l₁ в точке k₁.

Для определения видимости пря­мой и плоскости надо сравнить по­ложение в пространстве двух кон­курирующих точек, из которых одна принадлежит прямой, а вторая — плоскости. Например, возьмем на горизонтальной проекции точку 1 прямой AD и точку 3 прямой L. Горизонтальные проекции 1 и 3 этих точек совпадают. Судя по фронталь­ной проекции, точка 1 прямой AD расположена в пространстве выше и на горизонтальной проекции «за­крывает» точку 3. Следовательно, участок прямой 3 К₁ проходит под плоскостью и на горизонтальной проекции будет невидим. Аналогич­но определяется видимость другого участка прямой L. Для определения видимости на фронтальной проекции нужно взять две фронтально-конку­рирующие точки, из которых одна принадлежит прямой, а другая — плоскости ABCD.

 

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ

Что­бы построить линию пересечения двух плоскостей, поступают следую­щим образом: берут в одной из плос­костей две любые прямые и строят точки пересечения их с другой плос­костью, т. е. сводят задачу к только что рассмотренной задаче на пере­сечение прямой с плоскостью обще­го положения.

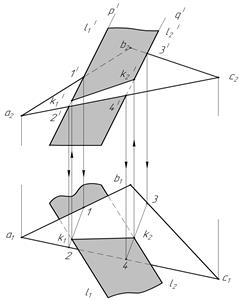
Рис. 11

На рис. 11 показано решение за­дачи на пересечение треугольника ABC с плоскостью, заданной двумя параллельными прямыми L₁ и L₂.

КОНТРОЛЬНАЯ РАБОТА №1

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1 (лист 1)

 

 

На чертеже формата А3 выполнить графическую работу в соответствии с номером варианта указанном в таблице 1-3.

 Заполнить основную надпись по образцу (рис. 12).

1. Построить проекции отрезка DK, принадлежащего плоскости АВС (табл. 1).

 

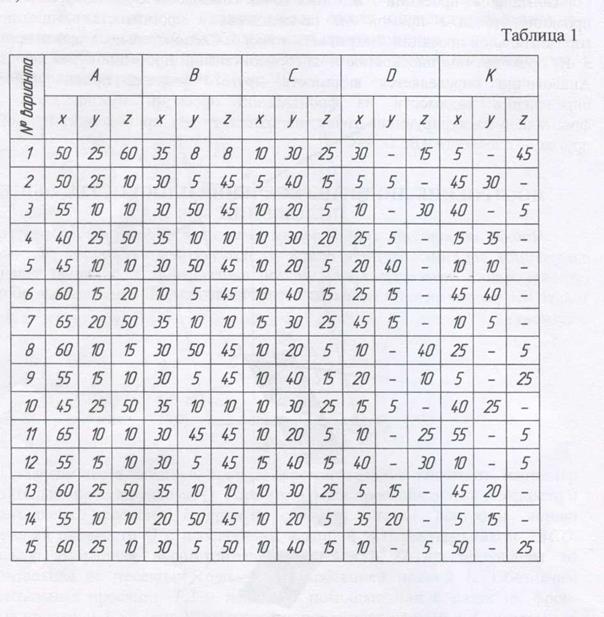
2. Построить по заданным координатам эпюр плоскости АВС и прямой MN. Найти точку пересечения прямой MN с плоскостью. Определить видимость (табл. 2).

 

Таблица 2

 

 

3. Построить проекции плоскостей АВС и DEF, найти линию пересечения. Определить видимость (табл. 3).

Таблица 3

 

 

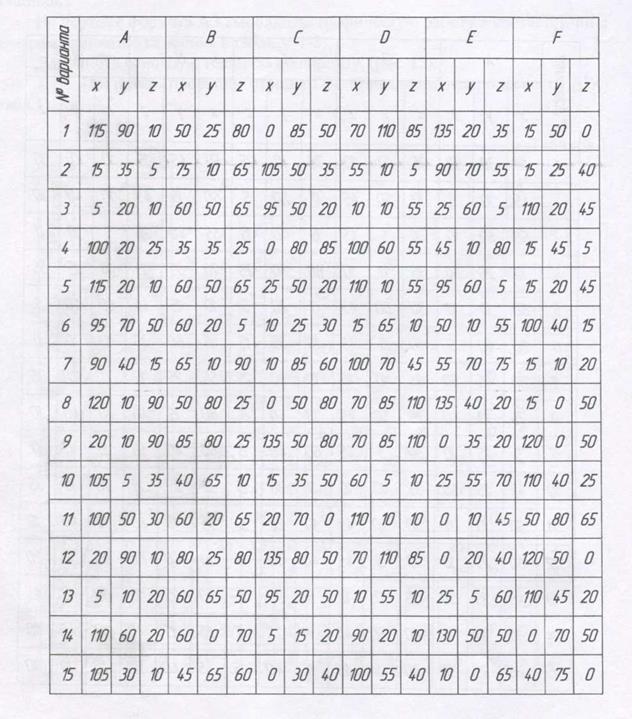
⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: