Построение на чертеже точки пересечения прямой с плоскостью и линии пересечения

ПОСТРОЕНИЕ НА ЧЕРТЕЖЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ И ЛИНИИ ПЕРЕСЕЧЕНИЯ

ДВУХ ПЛОСКОСТЕЙ

Построить точку пересечения прямой с плоскостью — значит най­ти точку, принадлежащую одновре­менно заданной прямой и плоскости. На рис. 7 такой общей точкой яв­ляется точка К.

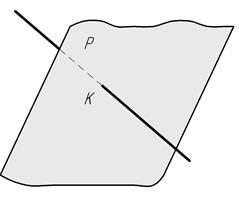
Рис. 7

Рассмотрим, как решается задача на построение точки пересечения прямой с проецирующей плоскостью.

Пусть необходимо построить точ­ку К пересечения прямой MN с плос­костью, заданной четырехугольни­ком ABCD (рис. 8).

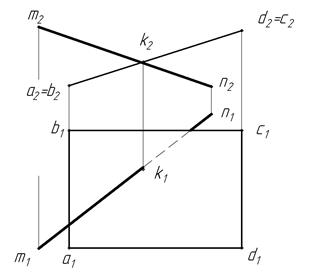
Рис. 8

Из чертежа видно, что плос­кость, определяемая прямоуголь­ником ABCD, — фронтально-проеци­рующая. Отсюда фронтальная про­екция плоскости — прямая линия a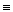₂ b₂ d₂ 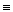с₂. Из свойств проецирую­щих плоскостей известно, что проек­ция любой точки, линии и плоской фигуры, лежащей в проецирующей плоскости, совпадает с проекцией этой плоскости на той плоскости про­екций, к которой заданная плоскость перпендикулярна. Поэтому фрон­тальная проекция к₂ точки К, лежа­щей в плоскости, заданной четырех­угольником ABCD, совпадает с фронтальной проекцией а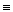₂  b₂ d₂ 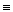c₂ плоскости. В пересечении фронтальной проекции m₂n₂ прямой с фронтальной проекцией a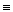₂ b₂ d₂ 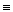с₂ плоскости находим фронтальную проекцию к₂ точки К. Горизонталь­ную проекцию к определяем при по­мощи линии связи к₁к₂. При этом сле­дует иметь в виду, что горизонталь­ная проекция к точки К будет ле­жать на горизонтальной проекции m₁n₁ прямой MN.

Теперь необходимо определить ви­димость прямой  MN относительно плоскости, заданной четырехуголь­ником ABCD. По фронтальной про­екции (рис. 8) заключаем, что часть прямой от точки М до точки К рас­положена над плоскостью (выше плоскости), поэтому на горизонталь­ной проекции она будет видима и изобразится основной сплошной ли­нией. Часть прямой от точки К не­видима, так как расположена под плоскостью. На горизонтальной про­екции она изобразится штриховой линией.

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ, ИЗ КОТОРЫХ ОДНА — ПРОЕ­ЦИРУЮЩАЯ

В общем случае для по­строения линии пересечения двух плоскостей необходимо построить какие-либо две точки, каждая из которых принадлежит обеим пло­скостям. Эти точки и будут опреде­лять искомую линию (рис. 9).

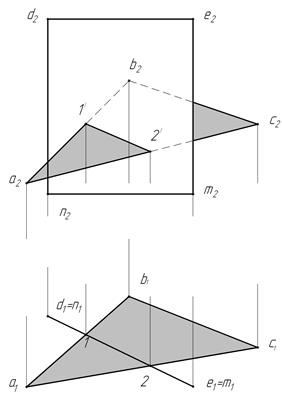
Рис. 9

Рассмотрим вначале пример по­строения линии пересечения таких двух плоскостей, из которых хотя бы одна проецирующая (рис. 9).

По чертежу заключаем, что плос­кость, определяемая четырехуголь­ником DEMN, проецирующая. Ее го­ризонтальная проекция — прямая линия. Точки, принадлежащие линии пересечения заданных плоскостей, можно найти как точки пересечения двух любых прямых одной плоско­сти с другой (например, прямых АВ и АС плоскости, заданной треуголь­ником ABC, с плоскостью, заданной четырехугольником DEMN). Таким образом, задача на построение ли­нии пересечения двух плоскостей сво­дится к предыдущей задаче — к построению точек пересечений прямой с плоскостью.

Поскольку в условии задачи плоскость горизонтально-проециру­ющая, то горизонтальные проекции точек 1 и 2 совпадают с горизонталь­ной проекцией d₁ n₁e₁ m₁ плоскости, заданной четырехугольником DEMN. Фронтальные проекции 1' и 2' определяются при помощи вертикальных линий связи. Они будут лежать на фронтальных проекциях а₂b₂ и а₂с₂.

На горизонтальной проекции вид­но, что часть треугольника ABC, а именно участок 1в₁с₁2, находится за плоскостью четырехугольника DEMN. На фронтальной проекции он будет частично невидим.