 |
Прямая, параллельная плоскости
|
|
|
|
ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.
Чтобы изобразить такую прямую, надо в плоскости задать прямую и параллельно ей провести требуемую. Пусть через точку А (рис. 13) необходимо провести прямую АВ, параллельную плоскости Р, заданной треугольником DEK.
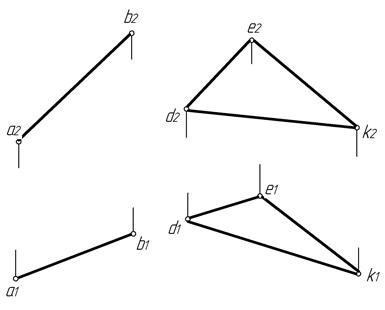
Рис. 13
Для этого через фронтальную проекцию а2 точки А проведем фронтальную проекцию а2b2 искомой прямой параллельно фронтальной проекции любой прямой, лежащей в плоскости Р, например прямой DE (a2b2//d2e2). Через горизонтальную проекцию а1 точки А параллельно d1e1 проводим горизонтальную проекцию a1b1 искомой прямой АВ (a1b1 // d1e1). Прямая АВ параллельна плоскости Р, заданной треугольником DEK.
Можно легко показать, что через данную точку можно провести сколько угодно прямых, параллельных заданной плоскости.
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
При решении задач в начертательной геометрии часто приходится проводить плоскость параллельно заданной. Как выполнить такое построение на чертеже?
Установлено, что две плоскости будут параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
На рис. 14 изображены две параллельные плоскости, заданные прямоугольниками ABCD и 1— 2 — 3 — 4. Пересекающиеся прямые
АВ и АС одной плоскости соответственно параллельны двум пересекающимся прямым 1 — 2 и 2 —3 другой.
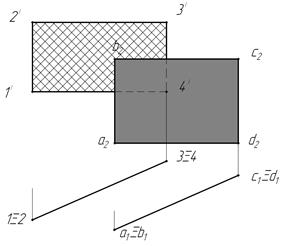
Рис. 14
Плоскости, изображенные на рис. 15, также параллельны, так как пересекающиеся прямые DE и ЕК плоскости, заданной треугольником DEK, соответственно параллельны пересекающимся прямым АВ и ВС плоскости, заданной треугольником ABC (AB//DE и ВС//ЕК).
|
|
|
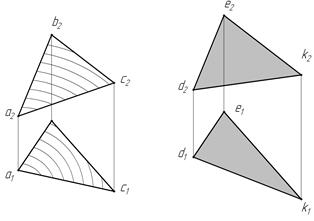
Рис. 15
На чертеже параллельны между собой фронтальные (a2b2 // d2e2 и b2c2 // e2k2) и горизонтальные (a1b1 // d1e1 и b1c1 // e1k1) проекции пересекающихся прямых.
ИЗОБРАЖЕНИЕ ПРЯМОЙ, ПЕРПЕНДИКУЛЯРНОЙ
К ПЛОСКОСТИ
Из элементарной геометрии известно, что прямая будет перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в данной плоскости (рис. 16).
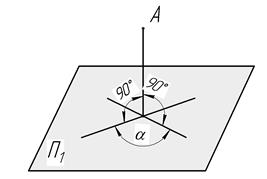
Рис. 16
Однако прямой угол (в данном случае между прямой, лежащей в плоскости, и перпендикуляром к ней) проецируется в истинную величину (90°) лишь в том случае, если одна из его сторон параллельна плоскости проекций. Поэтому, чтобы построить на чертеже перпендикуляр к плоскости, нужно брать в ней не любые прямые, а прямые, параллельные плоскостям проекций, т. е. прямые уровня — горизонтали и фронтали. Проводить перпендикуляр нужно к этим прямым.
Для того чтобы прямая была перпендикулярна к плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция — к фронтальной проекции фронтали плоскости.
Если, например, через заданную точку D необходимо провести прямую L, перпендикулярную к плоскости, заданной треугольником ABC (рис. 17), следует выполнить такие построения:
1) провести в плоскости, заданной треугольником ABC (рис. 17), прямые уровня — горизонталь A1 (a1 1, a 21′ ) и фронталь А 2 (а12, а22');
2) из горизонтальной проекции d1 точки D провести прямую, перпендикулярную к горизонтальной проекции a11 горизонтали это будет горизонтальная проекция l1 перпендикуляра;
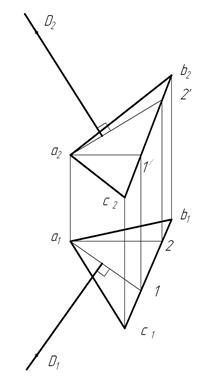
Рис. 17
3) из фронтальной проекции d2 точки D провести прямую l2, перпендикулярную к фронтальной проекции а22' фронтали, — фронтальную проекцию l2 перпендикуляра. Построенная прямая L (l1, l2) и есть перпендикуляр к плоскости, заданный треугольником ABC.
|
|
|
В рассмотренном примере на чертеже не найдено основание перпендикуляра. Чтобы это сделать, необходимо построить точку пересечения перпендикуляра с плоскостью, т. е. решить позиционную задачу на пересечение прямой с плоскостью.
|
|
|


