 |
Системы линейных уравнений
|
|
|
|
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

МАТРИЦЫ
Основные понятия
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде
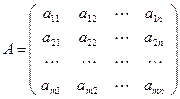
или, сокращенно,  , где
, где  (т.е.
(т.е.  ) – номер строки,
) – номер строки,  (т.е.
(т.е.  ) – номер столбца. Числа
) – номер столбца. Числа  , составляющие матрицу, называются ее элементами. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
, составляющие матрицу, называются ее элементами. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
 Матрицу А называют матрицей размера m × n и пишут
Матрицу А называют матрицей размера m × n и пишут  .
.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е.
 , если
, если  , где
, где  ,
,  .
.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера n × n называют матрицей n - го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.

Пример 1.1.
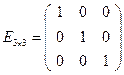
− единичная матрица 3-го порядка.

 − единичная матрица n -го порядка.
− единичная матрица n -го порядка.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Имеет вид
 .
.
 В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

 ,
,  .
.
 Матрица размера 1 × 1, состоящая из одного числа, отождествляется с этим числом, т.е.
Матрица размера 1 × 1, состоящая из одного числа, отождествляется с этим числом, т.е. 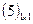 есть 5.
есть 5.
|
|
|
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначается  .
.
Так, если  , то
, то  , если
, если 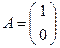 , то
, то  .
.
Транспонированная матрица обладает следующим свойством:  .
.
Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц  и
и  называется матрица
называется матрица 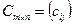 такая, что
такая, что 
 .
.

Пример 1.2.
 .
.
Аналогично определяется разность матриц.
Умножение на число
Произведением матрицы  на число k называется матрица
на число k называется матрица  такая, что
такая, что 
 .
.
 Пример 1.3.
Пример 1.3.
 , k = 2,
, k = 2,  .
.
Матрица  называется противоположной матрице А.
называется противоположной матрице А.
Разность матриц А – В можно определить так: А – В = А + (-В).
Операции сложения матриц и умножения на число обладают следующими свойствами:
- А + В = В + А;
- А + (В + С) = (А + В) + С;
- А + 0 = А;
- А – А = 0;
- 1 · А = А;
- α · (А + В) = αА + αВ;
- (α + β) · А = αА + βА;
- α · (βА) = (αβ) · А,
где А, В, С – матрицы, α и β – числа.
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
● перестановка местами двух параллельных рядов матрицы;
● умножение всех элементов ряда матрицы на число, отличное от нуля;
● прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
|
|
|
 .
.
 Пример 1.4. Привести к каноническому виду матрицу
Пример 1.4. Привести к каноническому виду матрицу
 .
.
 Решение: Выполняя элементарные преобразования, получаем
Решение: Выполняя элементарные преобразования, получаем
 | |||||
 | |||||
 | |||||
 ~
~ 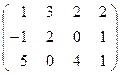 ~
~  ~
~

 ~
~ 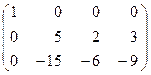 ~
~  ~
~

 ~
~  ~
~  .
.
Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что
 , где
, где  ,
,
т.е. элемент i -ой строки и k -го столбца матрицы произведения C равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы k -го столбца матрицы В.
Получение элемента  схематически изображается так:
схематически изображается так:
 |
 .
.
Если матрицы А и В квадратные одного размера, то произведение А В и В А всегда существует. Легко показать, что А · Е = Е · А = А, где А – квадратная матрица, Е – единичная матрица того же размера.

Пример 1.5.  .
.
Пример 1.6.  ,
,  . Тогда произведение А · В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение В × А, которое считают следующим образом:
. Тогда произведение А · В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение В × А, которое считают следующим образом:
 .
.
Матрицы А и В называются перестановочными, если АВ = ВА.
Умножение матриц обладает следующими свойствами:
- А · (В · С) = (А · В) · С;
- А · (В + С) = АВ + ВС;
3. (А + В) · С = АС + ВС;
4. α(АВ) = (αА)В.
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
- (А + В)Т = АТ + ВТ;
- (АВ)Т = ВТ + АТ.
ОПРЕДЕЛИТЕЛИ
Основные понятия
Квадратной матрице А порядка n можно сопоставить число det A (или |A|, или Δ), называемое ее определителем следующим образом:
- n = 1. А =
 ;
;  .
. - n = 2.
 ;
; 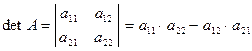 .
. - n = 3.
 ;
; 
 .
.
Определитель матрицы А также называют его детерминантом. Правило вычисления детерминанта матрицы порядка N является довольно сложным для восприятия и применения. Однако, известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство определителей 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.
|
|
|
Вычисление определителя 2-го порядка иллюстрируется схемой:

 .
.
 Пример 2.1. Найти определители матриц
Пример 2.1. Найти определители матриц
 и
и  .
.
 Решение:
Решение:
 ;
;

 .
.
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

 .
.
 | |||
 |
Пример 2.2. Вычислить определитель матрицы
 .
.
 Решение:
Решение: 

 .
.
Свойства определителей
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменяется, если его строки заменить столбцами, и наоборот.
Иными словами
 ,
, 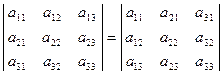 .
.
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,
 .
.
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,

 .
.
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.

Пример 2.3. Доказать, что
 .
.
 Решение: Действительно, используя свойства 5, 4 и 3 получим
Решение: Действительно, используя свойства 5, 4 и 3 получим

 .
.
 Дальнейшие свойства определителя связаны с понятиями минора и алгебраического дополнения.
Дальнейшие свойства определителя связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента 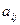 определителя n -го порядка называется определитель n – 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
определителя n -го порядка называется определитель n – 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  .
.
|
|
|
 Так, если
Так, если  , то
, то  ,
,  .
.
Алгебраическим дополнением элемента 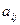 определителя называется его минор, взятый со знаком «плюс», если сумма
определителя называется его минор, взятый со знаком «плюс», если сумма  – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
– четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.
Так, 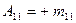 ,
, 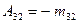 .
.
Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-го порядка. В этом случае свойство 7 означает, что

 .
.
В самом деле, имеем

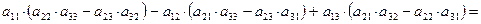
 .
.
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример 2.4. Вычислите определитель матрицы
 .
.
 Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.
Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.
 |




 .
.
Свойство 8. Сумма произведений какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,  .
.
НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
Основные понятия
Пусть А – квадратная матрица n -го порядка

 .
.
Квадратная матрица А называется невырожденной, если определитель  не равен нулю:
не равен нулю:  . В противном случае (
. В противном случае ( ) матрица А называется вырожденной.
) матрица А называется вырожденной.
 Матрицей, союзнойк матрице А, называется матрица
Матрицей, союзнойк матрице А, называется матрица
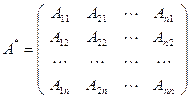 ,
,
где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 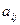 данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
 Матрица
Матрица  называется обратной матрице А, если выполняется условие:
называется обратной матрице А, если выполняется условие:
 , (3.1)
, (3.1)
где Е – единичная матрица того же порядка, что и матрица А. Матрица  имеет те же размеры, что и матрица А.
имеет те же размеры, что и матрица А.
Обратная матрица
 | |||
 |
Приведем доказательство для случая матрицы 3-го порядка. Пусть
 , причем
, причем  .
.
Составим союзную матрицу

и найдем произведение матриц  :
:

т.е.
 (3.2)
(3.2)
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).
Аналогично убеждаемся, что
 . (3.3)
. (3.3)
Равенства (3.2) и (3.3) перепишем в виде
 и
и 
Сравнивая полученные результаты с определением (3.1), получим

 т.е.
т.е.  .
.
Отметим свойства обратной матрицы:
1.  ;
;
2.  ;
;
3. 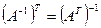 .
.
 Пример 3.1. Найти
Пример 3.1. Найти  , если
, если 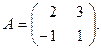
 Решение: 1) Находим
Решение: 1) Находим 
2) Находим  , поэтому
, поэтому
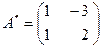 .
.
3) Находим  .
.
Проверка:


 .
.
Пример 3.2. Определить, при каких значениях λ существует матрица, обратная данной:

 Решение: Всякая невырожденная матрицы имеет обратную. Найдем определитель матрицы А:
Решение: Всякая невырожденная матрицы имеет обратную. Найдем определитель матрицы А:

 Если
Если  , т.е.
, т.е. 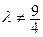 , то
, то  , то матрица А невырожденная, имеет обратную.
, то матрица А невырожденная, имеет обратную.
|
|
|

Пример 3.3. Показать, что матрица А является обратной для В, если
 ,
,  .
.
 Решение: Найдем произведение матриц А и В:
Решение: Найдем произведение матриц А и В:

 Аналогично В · А = Е. Следовательно, матрица А является обратной для В.
Аналогично В · А = Е. Следовательно, матрица А является обратной для В.
Ранг матрицы
Рассмотрим матрицу А размера m × n.

 .
.
 Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить
Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 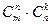 штук, где
штук, где  – число сочетаний из n элементов по k.)
– число сочетаний из n элементов по k.)
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рантом матрицы. Обозначается r, r (A) или rang A.
 Очевидно, что
Очевидно, что  , где
, где  – меньшее из чисел m и n.
– меньшее из чисел m и n.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример 3.4. Найти ранг матрицы:


 Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 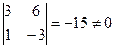 . Значит,
. Значит, 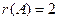 . Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
. Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменится при элементарных преобразованиях матрицы (см. с. 3).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Пример 3.5. Найти ранг матрицы

используя результаты примера 1.4.
 Решение: В примере 1.4. показано, что
Решение: В примере 1.4. показано, что
 ~
~  ,
,
то есть
 ~
~  .
.
 Таким образом, ранг матрицы А равен
Таким образом, ранг матрицы А равен 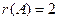 .
.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Основные понятия
Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

 где числа
где числа  называются коэффициентами системы, числа
называются коэффициентами системы, числа  – свободными членами. Подлежат нахождению числа
– свободными членами. Подлежат нахождению числа  .
.
Такую систему удобно записывать в компактной матричной форме
|
Здесь А – матрица коэффициентов системы, называемая основной матрицей:
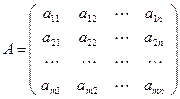 ,
,
 – вектор-столбец из неизвестных
– вектор-столбец из неизвестных  ,
,
 – вектор-столбец из свободных членов
– вектор-столбец из свободных членов  .
.
Произведение матриц  определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица  системы, дополненная столбцом свободных членов
системы, дополненная столбцом свободных членов
 .
.
 Решением системы называется n значений неизвестных
Решением системы называется n значений неизвестных  , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца  .
.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она ни имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:

Однородная система всегда совместна, так как  является решением системы. Это решение называется нулевым или тривиальным.
является решением системы. Это решение называется нулевым или тривиальным.
|
|
|



