 |
Решение систем линейных уравнений методом Гаусса
|
|
|
|
Одним из наиболее универсальных и эффективных методов решений систем линейных алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
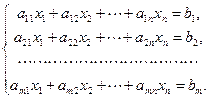(4.3)
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
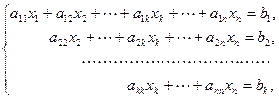
где 
. Коэффициенты 
называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных этой ступенчатой системы.
Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент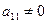 
(если 
, то первым в системе запишем уравнение, в котором коэффициент при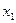 
отличен от нуля).
Преобразуем систему (4.3), исключив неизвестное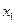 
во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на 
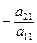и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 
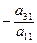и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
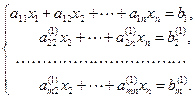
Здесь 
– новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом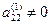 
, исключим неизвестное 
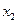из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида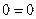 
, то их отбрасывают. Если же появится уравнение вида 
, а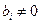 
, то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное 
через остальные неизвестные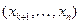 
; затем находим 
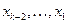. Придавая свободным неизвестным 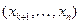произвольные значения, получим бесчисленное множество решений системы.
|
|
|
Замечания: 1. Если ступенчатая система оказывается треугольной, т.е. 
, то исходная система имеет единственное решение. Из последнего уравнения находим 
, из предпоследнего уравнения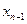 
, далее поднимаясь по системе вверх, найдем все остальные неизвестные 
.
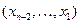2. На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент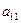 
был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на 
).
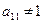Пример 4.4. Решить систему методом Гаусса:
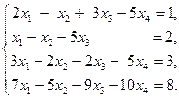
Решение: В результате преобразований над расширенной матрицей системы
~ 
~
~ 
~ 
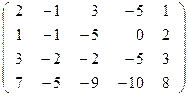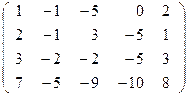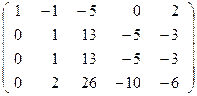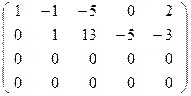
исходная система свелась к ступенчатой:
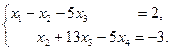
Поэтому, общее решение системы: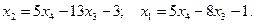 
Если положить, например, 
, то найдем одно из частных решений этой системы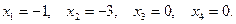 
Пример 4.5. Решить систему методом Гаусса:
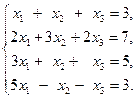
Решение: Произведем элементарные преобразования над строчками расширенной матрицы системы:
~ 
~ 
~ 
.
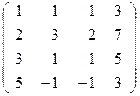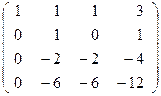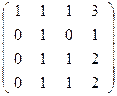Полученная матрица соответствует системе:
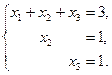
Осуществляя обратный ход, находим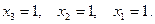 
Системы однородных линейных уравнений
Пусть дана система линейных однородных уравнений
Очевидно, что однородная система всегда совместна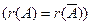 
, она имеет нулевое (тривиальное) решение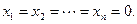 
При каких условиях однородная система имеет и ненулевые решения?
 | |||
 |
Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевидно,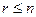 
. Пусть 
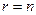. Тогда один из миноров размера 
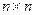отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: 
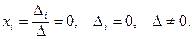Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то 
.
|
|
|
Достаточность.
Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.
Пусть дана однородная система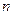 
линейных уравнений с 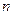неизвестными
 | |||||
 | |||||
 |
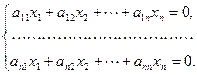
Если система имеет ненулевые решения, то 
. Ибо при 
система имеет единственное, нулевое решение. Если же , то ранг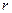 
основной матрицы системы меньше числа неизвестных, т.е. . И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример 4.6. Решить систему
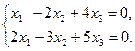
Решение: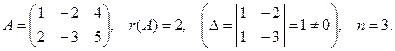 
Так как , то система имеет бесчисленное множество решений. Найдем их
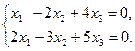
Стало быть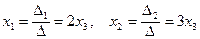 
– общее решение. Положив 
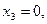получим одно частное решение: 
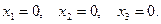Положив 
получаем второе частное решение: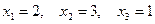 
и т.д.
Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
ВЕКТОРЫ
Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина изображается с помощью вектора.
Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А – начало вектора, а В – его конец, то вектор обозначается символом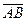 
или 
. Вектор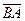 
(у него начало в точке В, а конец в точке А) называется противоположным вектору 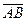. Вектор, противоположный вектору , обозначается 
.
Длиной или модулем вектора 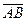называется длина отрезка и обозначается 
. Вектор, дина которого равна нулю, называется нулевым вектором и обозначается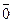 
. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через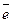 
. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается 
.
Векторы и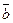 
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .
|
|
|
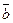Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
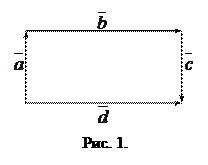Два вектора и 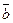называются равными ( = 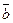), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
На рисунке 1 векторы образуют прямоугольник. Справедливо равенств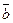о = 
, но 
. Векторы и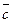 
– противоположные, 
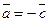. Равные векторы также называют свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны.
|
|
|
