 |
И перпендикулярности двух прямых
|
|
|
|
Пусть прямые 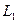 и
и 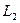 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 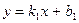 и
и  (см. рис. 46).
(см. рис. 46).
Требуется найти угол φ, на который надо повернуть в положительном направлении прямую 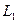 вокруг точки их пересечения до совпадения с прямой
вокруг точки их пересечения до совпадения с прямой 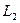 .
.

 Решение: Имеем
Решение: Имеем  (теорема о внешнем угле треугольника) или
(теорема о внешнем угле треугольника) или  Если
Если  , то
, то 
Но  , поэтому
, поэтому
|
(10.12)
откуда легко получим величину искомого угла.
 |
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая – второй, то правая часть формулы (10.12) берется по модулю, т.е. 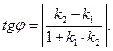
Если прямые 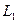 и
и 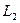 параллельны, то
параллельны, то  и
и  . Из формулы (10.12) следует
. Из формулы (10.12) следует  , т.е.
, т.е.  . И обратно, если прямые
. И обратно, если прямые 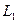 и
и 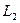 таковы, что
таковы, что  , то
, то  , т.е. прямые параллельны. Следовательно, условием параллельности двух прямых является равенство их угловых коэффициентов:
, т.е. прямые параллельны. Следовательно, условием параллельности двух прямых является равенство их угловых коэффициентов:  .
.
Если прямые 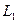 и
и 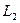 перпендикулярны, то
перпендикулярны, то  . Следовательно,
. Следовательно,  . Отсюда
. Отсюда  , т.е.
, т.е. 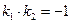 (или
(или  ). Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство
). Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство 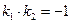 .
.
 Расстояние от точки до прямой
Расстояние от точки до прямой
Пусть заданы прямая L уравнением 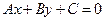 и точка
и точка  (см. рис. 47). Требуется найти расстояние от точки
(см. рис. 47). Требуется найти расстояние от точки  до прямой L.
до прямой L.
 Решение: Расстояние d от точки
Решение: Расстояние d от точки  до прямой L равно модулю проекции вектора
до прямой L равно модулю проекции вектора  , где
, где  – произвольная точка прямой L, на направление нормального вектора
– произвольная точка прямой L, на направление нормального вектора  . Следовательно,
. Следовательно,
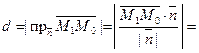
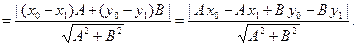
|
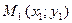 принадлежит прямой L, то
принадлежит прямой L, то 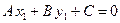 , т.е.
, т.е. 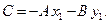 Поэтому
Поэтому
(10.13)
 что и требовалось получить.
что и требовалось получить.

Пример 10.3. Найти расстояние от точки 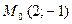 до прямой
до прямой 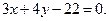
 Решение: По формуле (10.13) получаем
Решение: По формуле (10.13) получаем

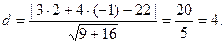
ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
Основные понятия
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
|
|
|
 (11.1)
(11.1)
Коэффициенты уравнения – действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11.1) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде чем переходить к этому утверждению, изучим свойства перечисленных кривых.
 11.2. Окружность
11.2. Окружность
Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке  называется множество всех точек М плоскости, удовлетворяющих условию
называется множество всех точек М плоскости, удовлетворяющих условию  . Пусть точка М в прямоугольной системе координат Оху имеет координаты
. Пусть точка М в прямоугольной системе координат Оху имеет координаты  , а
, а  – произвольная точка окружности (см. рис. 48).
– произвольная точка окружности (см. рис. 48).
Тогда из уравнения  получим уравнение
получим уравнение
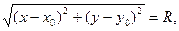
|
(11.2)
Уравнению (11.2) удовлетворяют координаты любой точки  данной окружности и не удовлетворяют координаты никакой точки, не лежащих на окружности.
данной окружности и не удовлетворяют координаты никакой точки, не лежащих на окружности.
Уравнение (11.2) называется каноническим уравнением окружности.
В частности, полагая  и
и  , получим уравнение окружности с центром в начале координат
, получим уравнение окружности с центром в начале координат 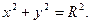
Уравнение окружности (11.2) после несложных преобразований примет вид  При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:
При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:
1) коэффициенты при 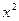 и
и  равны между собой;
равны между собой;
2) отсутствует член, содержащий произведение  текущих координат
текущих координат
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения  и
и  получим
получим
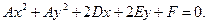 (11.3)
(11.3)
Преобразуем это уравнение:
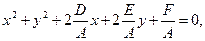
т.е.
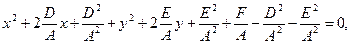
т.е.
 (11.4)
(11.4)
Отсюда следует, что уравнение (11.3) определяет окружность при условии,  Ее центр находится в точке
Ее центр находится в точке  , а радиус
, а радиус  . Если же
. Если же  , то уравнение (11.3) имеет вид
, то уравнение (11.3) имеет вид 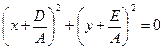 . Ему удовлетворяют координаты единственной точки
. Ему удовлетворяют координаты единственной точки  . В этом случае говорят: «окружность выродилась в точку» (имеет нулевой радиус).
. В этом случае говорят: «окружность выродилась в точку» (имеет нулевой радиус).
Если 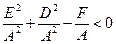 , то уравнение (11.4) а, следовательно, и равносильное уравнение (11.3) не определяет никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая часть – не отрицательна (говорят: «окружность мнимая»).
, то уравнение (11.4) а, следовательно, и равносильное уравнение (11.3) не определяет никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая часть – не отрицательна (говорят: «окружность мнимая»).
|
|
|
Эллипс
|
|
|





