 |
Поверхность и ее уравнение
|
|
|
|
Поверхность в пространстве, как правило, можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке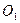 
есть геометрическое место всех точек пространства, находящихся от точки 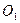на расстоянии R.
Прямоугольная система координат 
в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел x, y и z – их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе координат называется такое уравнение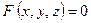 
с тремя переменными x, y и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные x, y и z в уравнении поверхности называются текущими координатами поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка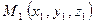 
на данной поверхности, достаточно подставить координаты точки 
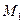в уравнение поверхности вместо переменных: если это координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют – не лежит.
Уравнение сферы
Найдем уравнение сферы радиуса R с центром в точке 
. Согласно определению сферы расстояние любой ее точки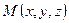 
от центра равен радиусу R, т.е. 
. Но 
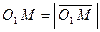, где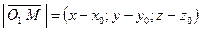 
. Следовательно,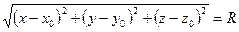 
или
|
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
|
|
|
Если центр сферы 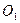совпадает с началом координат, то уравнение сферы принимает вид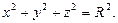 
Если же дано уравнение 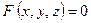, то оно, вообще говоря, определяет в пространстве некоторую поверхность.
Выражение «вообще говоря» означает, что в отдельных случаях уравнение 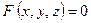может определять не поверхность, а точку, линию, или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».
Так, уравнению 
не удовлетворяют никакие действительные значения x, y и z. Уравнению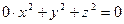 
удовлетворяют лишь координаты точек, лежащих на оси Ox (из уравнения следует: 
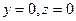, а х – любое число)
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
- Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
- Дано уравнение 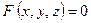. Исследовать форму поверхности, определяемой этим уравнением.
Уравнение линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.
Есл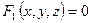и 
и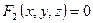 
– уравнения двух поверхностей, определяющих линию L то, координаты этой линии удовлетворяют системе двух уравнений с тремя неизвестными:
(12.1)
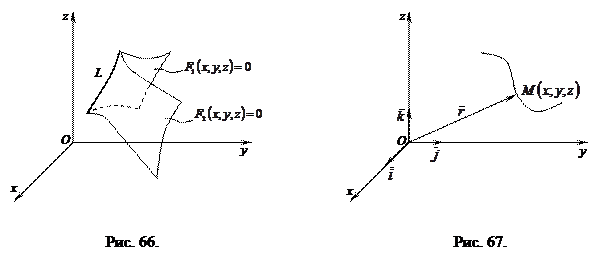Уравнения системы (12.1) называются уравнениями линии в пространстве. Например, 
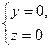есть уравнения оси Ox.
Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением
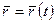(12.2)
 |
или параметрическими уравнениями
проекций вектора (12.2) на оси координат.
Например, параметрические уравнения винтовой линии имеют вид
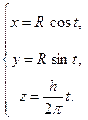
Если точка M равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка M описывает винтовую линию (см. рис. 68).
|
|
|
