 |
4.10. Метод корневого годографа
|
|
|
|
4. 10. Метод корневого годографа
Корневой годограф – это совокупность траекторий, по которым перемещаются корни характеристического уравнения в комплексной плоскости при изменении одного из варьируемых параметров системы.
Построив корневой годограф, можно выбрать такое значение варьируемого параметра системы, которое обеспечит желаемое расположение корней.
Допустим, что характеристическое уравнение замкнутой системы содержит варьируемы параметр К:
D(S) + KQ(S) = 0,
где D(S) и Q(S) – полиномы степени n и m соответственно. В частности, пусть например 
и Q(S)=1.
Для построения корневого годографа имеется ряд правил:
1. Корневой годограф содержит n симметричных относительно вещественной оси ветвей, которые при к=0 начинаются в точках, соответствующих корням уравнения D(S)=0, т. е. Si=-1/Ti (i=1, 2, 3).
2. m ветвей корневого годографа должно приходить в точки, соответствующие корням уравнения Q(S)=0. У нас m=0. n-m ветвей корневого годографа при увеличении К уходит в бесконечность вдоль асимптот, которые образуют (n-m)-лучевую симметричную звезду в центром на вещественной полуоси.
3.
| Рис 4. 10. 1 |
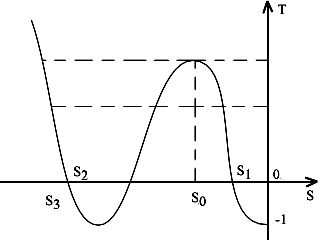Траектории вещественных корней можно определить, построив график вспомогательной функции 
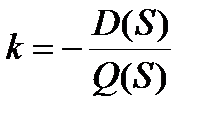. Задаваясь на этом графике значениями К, можно определить соответствующие этим значениям корни характеристического уравнения. Точка максимума этой функции определяет координату точки отрыва корней от вещественной оси и перехода их в комплексную плоскость.
4. Для построения траекторий комплексных корней (если они есть в характеристическом уравнении) разработаны свои правила. При этом точки пересечения ветвей корневого годографа с мнимой осью соответствует колебательной границе устойчивости системы, когда ее варьируемый параметр К имеет критическое значение.
|
|
|
Корневой годограф рассматриваемой САР приведен на рис.:
| Рис 4. 10. 2 |
4. 11. Интегральные оценки качества переходных процессов
Эти оценки представляют собой определенные интегралы от переходной погрешности x(t)=dПЕР(t)=yУСТ(t)-y(t). Интегральные оценки делятся на линейные и квадратичные.
Общий вид линейной интегральной оценки:
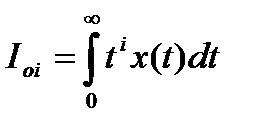- моменты i-го порядка i=0, 1, 2.
| Рис 4. 11. 2 |
| Рис 4. 11. 1 |
может служить мерой длительности переходного процесса, если он является монотонным. Геометрически эта оценка представляет собой площадь под кривой x(t).
Если же процесс не является монотонным, то при вычислении этой оценки происходит частичная компенсация площадей одного знака площадями другого знака.
В итоге оценка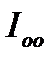 
может иметь достаточно малое значение при достаточно большой длительности переходного процесса. Именно поэтому линейные оценки моментов первого порядка и выше содержат коэффициент ti, который налагает штраф на длительность переходного процесса. При этом штраф тем больше, чем выше степень i.
Вычисление значений линейных интегральных оценок можно осуществлять с помощью изображения по Лапласу переходной погрешности:
x(S) = L{x(t)} = 
или разлагая в ряд по степеням St:
С другой стороны при разложении по степеням S:
Из сопоставления полученных выражений находим:
; 
; 
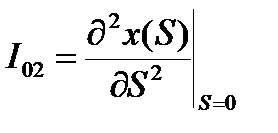и т. д.
Общий вид квадратичной интегральной оценки:
эти оценки характеризуют длительность переходных процессов. Где t00=1 и x(0)(t)=x(t).
Такие оценки применимы как к монотонным, так и к колебательным переходным процессам, так как инвариантны к знаку переходной погрешности.
При n=0 получается простейшая квадратичная оценка 
, которая обращается в нуль при ступенчатом процессе. Однако, эта оценка может иметь достаточно малое значение и при большой колебательности переходного процесса.
|
|
|
| x(0)e-t/t1 |
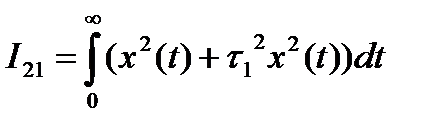, которая не может иметь малого значения при большой колебательности переходного процесса. Абсолютный минимум этой оценки соответствует экспоненте с постоянной времени t1.
Вычисление квадратичных оценок осуществляется по формуле Релея:
| Рис 4. 11. 3 |
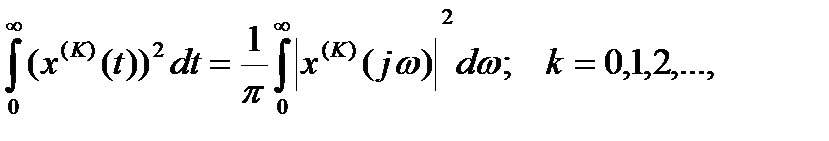где x(jw)-частотный спектр соответствующей функции времени x(t), 
, а x(S)=L{x(t)}.
При этом, если x(K)(jw) – дробно-рациональная функция, то значение соответствующего интеграла в формуле Релея можно найти по табличной алгебраической формуле через коэффициенты подынтегральной функции в справочной литературе.
|
|
|
