После начального периода t¢¢ скорость подъёма температуры на поверхности и оси становится одинаковой и происходит параллельный подъём температур во всех точках. Изменение температур во времени имеет линейный характер. Этот период называется регу

После начального периода t¢ ¢ скорость подъёма температуры на поверхности и оси становится одинаковой и происходит параллельный подъём температур во всех точках. Изменение температур во времени имеет линейный характер. Этот период называется регулярным.

После начального периода в теле по его толщине устанавливается параболическое распределение температур   [t = t_c ± Dt× (x / S)²], которое сохраняется и далее.

Решение уравнения теплопроводности при двухстороннем нагреве бесконечной пластины толщиной 2S имеет следующий вид:

t =          (29)

где e = p× ℓ (ℓ = 1, 2, 3, × × × ).

Это решение в общем виде запишется:

t×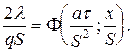

Значения функции Ф  приведены в литературе.

Для цилиндра радиусом R  решение имеет вид

t =                (30)

или в общем виде                    t

Из анализа кривых температур видно, что при t > 0, 3× S²/ а - для пластины и t > 0, 25× R²/ а  для цилиндра изменения температуры принимают прямолинейный характер, т. е. содержащий экспоненциальную функцию член в формулах (29) и (30) может быть отброшен.

Тогда из уравнений (29)  и (30) общая расчётная формула будет иметь вид:

 

 

для пластины

t = ;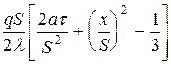

для цилиндра

t =.

Для поверхности пластины

tпов =.                               (31)

Для поверхности цилиндра

tпов =.                               (32)

Для центра пластины

t_с = .

 

Для   центра цилиндра

tс =.

Разность температур между поверхностью и центром:

для пластины

Dtm = tпов - tc =  = const;

для цилиндра

Dtm = tпов - tc =  = const

Средняя температура по сечению пластины

1

2

t_cр = t_пов -  Dt_m = t_с + Dt_m.

Средняя температура по сечению цилиндра

1

1

t_cр = t_пов - Dt_m = t_с + Dt_m.

Линия средней температуры пластины пересекает параболическую кривую распределения температур тела в точке, которая отстоит от начала координат по оси х на расстоянии х₁ = 0, 577× S

Линия средней температуры цилиндра пересекает параболическую кривую распределения температур тела в точке, которая отстоит от начала координат на расстоянии r₁ = 0, 707× R.

41. ВРЕМЯ ЗАПАЗДЫВАНИЯ

Инерционное время- это время, в течение которого тепловая волна, идущая от поверхности, практически достигает середины тела при симметричном нагреве или другой точки тела, где температура минимальная, при несимметричном нагреве.

Инерционное время ( время начала подъёма температуры на оси тела ) пропорционально квадрату толщины нагреваемого слоя, обратно пропорционально температуропроводности материала, и зависит от формы тела. Оно определяется по зависимости

t¢ = S² / k× а,

где k = k₁× k₂× k₃;

k₁ - коэффициент формы ( для пластины равен 1, цилиндра -2,  

шара 3).

k2- коэффициент усреднения тепловых потоков по толщине тела (для пластины - 2, цилиндра - 2, шара -2).

k₃ - коэффициент усреднения разности температур в теле (для пласти-

ны - 3, цилиндра - 2, шара - 1, 67).

Следовательно, инерционное время для пластины   t¢ = S² / 6× а, для цилиндра   t¢ = R² / 8× а.

Температура поверхности пластины в конце начального участка нагрева определим, подставляя в формулу (31)  значение t¢ > 0, 3× S² / а.

tпов¢ =  = × 1, 27 = 1, 27× Dtm.

Аналогично находится температура поверхности цилиндра в конце начального участка нагрева (t¢ > 0, 25× R² / а)

tпов¢ = 1, 5× = 1, 5× Dtm.

Температура середины пластины в конце начального участка нагрева

tс¢ = tпов¢ -  = 1, 27× Dtm - Dtm = 0, 27× Dtm.

Температура середины цилиндра в конце начального участка нагрева

tс¢ = tпов¢ - = 0, 5× Dtm.

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: