 |
1. Учет случайности характера взаимодействия переменных в экономических объектах. Общий вид эконометрической модели.
|
|
|
|
Оглавление
1. Учет случайности характера взаимодействия переменных в экономических объектах. Общий вид эконометрической модели. 2
2. Оценка уравнения парной регрессии с помощью метода наименьших квадратов. 3
3. Понятие качества спецификации модели. Методы оценки качества спецификации. 5
4. Ошибки спецификации моделей, их последствия и способы устранения. 6
5. Показатели качества спецификации линейной модели. 8
6. Фиктивные переменные и особенности их использования в моделях. 12
7. Этапы построения моделей, их практическое содержание и особенности. 12
8. Понятие качества спецификации модели, тестирование качества спецификации модели. 12
9. Эконометрика как наука, определение, основные цели и задачи. 12
10. Понятие гетероскедастичности, оценивание гетероскедастичных моделей, взвешенный метод наименьших квадратов. 12
11. Базовые понятия эконометрики: экономический объект, переменные объекта и их взаимосвязи. Примеры экономических моделей. 13
12. Автокорреляция случайных возмущений, их последствия, взвешенный метод наименьших квадратов. 13
13. Классификация переменных эконометрических моделей. 13
14. Расчет стандартных ошибок параметров уравнения парной регрессии и точности прогнозирования. 13
15. Теорема Гаусса-Маркова, основные допущения и предпосылки, их практическое содержание и назначение. 13
16. Нелинейная регрессия. Нелинейные модели и их линеаризация. 13
17. Использование фиктивных переменных сдвига в регрессионных моделях. 13
18. Понятие адекватности экономических моделей. Проверка статистической гипотезы об адекватности модели. 13
19. Проверка статистических гипотез. Оценка статистической значимости параметров уравнения множественной регрессии. 13
|
|
|
20. Тестирование моделей на присутствие автокорреляции. 13
21. Требования, предъявляемые к оценкам параметров моделей, 13
22. Классификация переменных эконометрических моделей, 13
23. Автокорреляция в уравнениях множественной регрессии, признаки ее наличия и последствия, Оценка параметров уравнения множественной регрессии с автокоррелированными остатками, 13
24. Последствия нарушения предпосылок теоремы Гаусса-Маркова. 13
25. Тестирование моделей на наличие гетероскедастичности, 13
26. Требования, предъявляемые к оценкам параметров моделей, 13
27. Понятие адекватности экономических моделей, Проверка статистической гипотезы об адекватности модели, 13
28. Линейная модель парной регрессии, Оценка параметров модели с помощью метода наименьших квадратов (МНК), 13
29. Построение нелинейных экономических моделей. 13
30. Принципы спецификации эконометрических моделей. 14
31. Проверка статистических гипотез, Оценка статистической значимости параметров уравнения множественной регрессии. 14
32. Ошибки спецификации моделей, их последствия и способы устранения, 14
33. Показатели качества спецификации линейной модели. 14
1. Учет случайности характера взаимодействия переменных в экономических объектах. Общий вид эконометрической модели.
Для обеспечения однозначной зависимости между эндогенной и экзогенными переменными в уравнение модели вводится еще одна переменная, которую называют «случайное возмущение» или «остаток». Возникает вопрос о причинах обязательного присутствия в эконометрических регрессионных моделях случайного фактора (отклонения). Среди таких причин выделим наиболее существенные.
1)Невключение в модель всех объясняющих переменных.
|
|
|
2)Неправильный выбор функциональной формы модели (из-за слабой изученности процесса или из-за его переменчивости).
3)Агрегирование переменных.
Во многих моделях рассматриваются зависимости между факторами, которые сами представляют сложную комбинацию других, более простых переменных.
4)Ошибка измерений.
5)Ограниченность статистических данных.
Зачастую строятся модели, выражаемые непрерывными функциями. Но при этом используется набор данных, имеющих дискретную структуру. Это несоответствие находит отражение в случайном отклонении.
6)Непредсказуемость человеческого фактора (эта причина может " испортить" самую качественную модель).
Случайная компонента модели является отражением влияния всех описанных выше причин и не только их. Список может быть дополнен.
Модели, которые в своем составе содержат случайные возмущения, называются эконометрическими
Общий вид:
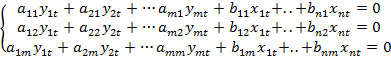
2. Оценка уравнения парной регрессии с помощью метода наименьших квадратов
Парная регрессия позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным, которая может описываться уравнениями следующего вида:
• прямой (ух = а0 а, *)-
• гиперболы ^ух = а0 а, -ь^;
• параболы {ух = а0+ ахх+ а2х2) и т. д.
Определить тип уравнения можно, исследуя зависимость графически. Однако существуют более общие рекомендации, позволяющие определять форму связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают
одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи — гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и при котором минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
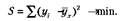
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
|
|
|
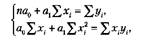
где п — объем исследуемой совокупности (число единиц наблюдения).
В уравнении регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а, показывает, насколько в среднем изменяется значение результативного признака при изменении факторного признака на единицу собственного измерения.
Пример. Имеются следующие данные об инвестициях в основной капитал и полной учетной стоимости основных фондов субъектов Центрального федерального округа РФ в 2010 г. (исключая Москву и Московскую область) (табл. 7. 4).
|
|
|


