 |
4. Ошибки спецификации моделей, их последствия и способы устранения.
|
|
|
|
4. Ошибки спецификации моделей, их последствия и способы устранения.
Возможные ошибки спецификации модели:
Неправильный выбор вида уравнения регрессии: Пусть на первом этапе была сделана спецификация модели в виде:
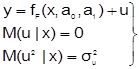
в которой функция fF(x, a0, a1) выбрана не верно. Предположим, что
yT=fT(x, a0, a1)+v – правильный вид функции регрессии. Тогда справедливо выражение:
.
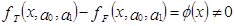Из выражения следует:
Иными словами, математические ожидания эндогенной переменной, полученные с помощью функций fT и fF не совпадают, т. е. первая предпосылка теоремы Гаусса-Маркова M(ulx)=0 не выполняется. Следовательно, в результате оценивания такой модели параметры а0 и а1 будут смещенными. В таком случае следует, используя диаграмму рассеивания, выбрать из арсенала моделей функций регрессии более подходящую кандидатуру и повторить процедуру построения регрессионной модели.
В уравнение регрессии включена лишняя (незначимая) переменная: Пусть на этапе спецификации в модель включена «лишняя» переменная, например, X2:
«Правильная» спецификация должна иметь вид:
Последствия: 1) Оценки параметров а0, а1, а2 останутся несмещенными, но потеряют свою эффективность (точность). 2) Увеличивается ошибка прогноза по модели
как за счет ошибок оценок коэффициентов и σ u, так и за счет последнего слагаемого.
Диагностика: В моделях множественной регрессии необходимо для каждого коэффициента уравнения проверять статистическую гипотезу
H0: ai=0.
Для этого достаточно оценить дробь Стьюдента
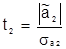
и сравнить ее значение с критическим значением распределения Стьюдента, которое вычисляется по значению доверительной вероятности и значению степени свободы n2 = n – (k+1). Если неравенство справедливо, то переменная принимается незначимой и может быть удалена из спецификации модели.
|
|
|
В уравнении регрессии пропущена значимая переменная:
.
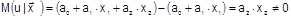Последствия такие же, как и в первом случае: получаем смещенные оценки параметров модели. Для устранения необходимо вернуться к изучению особенностей поведения экономического объекта, выявить опущенные переменные и дополнить ими модель.
Проблемы в использовании переменных:
Не возможно получение данных по переменной.
Не возможно измерить количественно переменную. Такие ситуации характерны для переменных социально-экономического характера. Выход из ситуации – подбор переменной заместителя. В качестве замещающей переменной часто используется время и лаговые переменные.
5. Показатели качества спецификации линейной модели
Основным инструментом оценивания параметров линейной модели множественной регрессии являются процедуры, сформулированные в теореме Гаусса – Маркова.
Недостаточно только вычислить значения оценок входящих в модель параметров, необходимо еще подтвердить качество параметров и модели в целом. Другими словами, необходимо провести анализ полученных результатов.
Начнем анализ результата оценивания модели с ответа на вопрос: насколько качественно был выполнен первый этап построения модели, а именно, не допустили ли мы ошибку, записывая спецификацию модели? На этапе спецификации модели есть возможность допустить две ошибки:
- 1) неправильно выбрать вид поведенческой части модели (функции регрессии);
- 2) неправильно выбрать набор экзогенных переменных, введенных в спецификацию модели.
Действительно, при спецификации модели принято ограничение об использовании только линейных алгебраических уравнений. Но вполне может оказаться, что модель существенно нелинейная (см. производственную функцию Кобба – Дугласа). Кроме того, в результате анализа поведения экономического объекта в спецификацию введем набор экзогенных переменных, который по предположению влияет на формирование эндогенной переменной. Здесь тоже возможно появление ошибок: может оказаться, что все выбранные переменные не оказывают влияния на величину эндогенной переменной или часть из них.
|
|
|
Тестирование качества спецификации модели направлено па выявление факторов, не оказывающих влияния на формирование эндогенной переменной.
Начнем обсуждение проблемы с примера уравнения парной регрессии.
Имеем спецификацию модели в виде
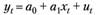( 6. 1 )
и предполагаем, что предпосылки теоремы Гаусса – Маркова выполнены.
Тогда модель (6. 1) можно записать в виде
(6. 2)
где
В уравнении (6. 2) первое слагаемое – это вклад в значение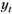 
, вызванный изменениями регрессора 
, а второе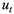 
– влияние случайных факторов, которые не связаны с изменениями регрессора.
Отсюда, вытекает идея тестирования. Необходимо установить, какое из слагаемых вносит наибольший вклад в общий разброс наблюдаемых значений эндогенной переменной. Характеристикой разброса случайной переменной служит дисперсия. Следовательно, необходимо определить, какое из слагаемых превалирует в функции дисперсии эндогенной переменной. Найдем дисперсию функции (6. 2):
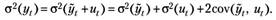(6. 3)
Найдем значение последнего слагаемого (6. 3):
(6. 4)
Первое слагаемое (6. 4) равно нулю, так как ковариация между константой и случайной величиной равна нулю, второе слагаемое равно нулю в силу четвертой предпосылки теоремы Гаусса – Маркова.
В результате получаем:
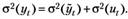(6. 5)
Выражение (6. 5) можно представить в виде
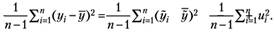(6. 6)
Введем следующие обозначения:
- –
-общая сумма квадратов (Total Sum Squares), - –
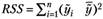регрессионная сумма квадратов (Regression Sum, Squars), - –
сумма квадратов ошибок (Error Sum Squares).
Тогда выражение (6. 6) можно записать как
(6. 7)
Замечание. Равенства (6. 6) и (6. 7) имеют место, если в модели присутствует параметр 
В качестве меры влияния регрессора на формирование значения эндогенной переменной у вводится коэффициент детерминации как отношение регрессионной суммы квадратов к общей сумме квадратов:
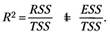(6. 8)
Область определения коэффициента детерминации – отрезок от нуля до единицы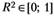 
|
|
|
Коэффициент детерминации показывает, какая доля изменения зависимой переменной обусловлена изменениями объясняющей переменной.
Если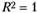 
, т. е. RSS = TSS, означает, что регрессор д: полностью обеспечивает весь размах изменения переменной у. В этом случае говорят, что спецификация модели, абсолютно качественная. Случайное возмущение во всех наблюдениях равно нулю.
Наоборот, если 
, т. е. ESS = TSS т. е. означает, что весь размах изменения переменной у есть следствие воздействия неучтенных случайных факторов. В этом случае говорят, что спецификация модели абсолютно некачественная. Регрессор не оказывает влияния на формирование эндогенной переменной.
С учетом сделанного выше замечания необходимо иметь в виду, что коэффициент детерминации 
имеет смысл только при наличии свободного коэффициента 
в спецификации линейно аддитивной модели. Если параметр 
отсутствует в спецификации модели, из-за невыполнения тождества (6. 7), значение 
, вычисленное по формуле (6. 8), может оказаться и больше единицы и даже отрицательным.
Можно показать, что в случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции между переменными у и х.
Коэффициент детерминации – величина случайная, так как его значение вычислено по случайной выборке. Следовательно, для тестирования гипотезы о том, что выбранный регрессор не оказывает влияние на формирование значения эндогенной переменной, согласно алгоритму проверки статистических гипотез, необходимо создать случайную переменную, связанную с гипотезой, закон распределения которой был бы известен.
Можно показать, что если случайное возмущение распределено нормально 
, то случайная величина 
подчиняется нормальному закону распределения. Тогда для проверки гипотезы 
в качестве статистики принимается переменная 
, которая вычисляется по правилу:
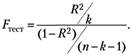(6. 9)
Здесь: п – объем выборки; k – количество регрессоров в модели (в нашем случае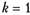 
); 
– коэффициент детерминации.
Переменная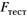 
подчиняется закону распределения Фишера с параметрами 
и ( 
). Приняв значение доверительной вероятности, например, 
, вычисляется критическое значение для переменной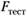 
|
|
|
Если имеет место неравенство
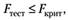(6. 10)
то гипотеза о том, что регрессор х не влияет на формирование значения эндогенной переменной у, принимается. Если условие (6. 10) не выполняется, то принимается альтернативная гипотеза о том, что регрессор х существенно влияет на формирование величины у.
Замечание. Значения коэффициента детерминации и статистики 
вычисляются функцией " ЛИНЕЙН" (см. табл. 5. 1).
Пример. Рассмотрим модель зависимости сбережений граждан от размера располагаемого дохода в Великобритании.
Исходные данные для построения модели (выборка наблюдений), а также результат работы функции " ЛИНЕЙН" приведены в табл. 6. 1.
Таблица 6. 1
|
|
|
