13. Классификация переменных эконометрических моделей.

13. Классификация переменных эконометрических моделей.        

При построении эконометрических моделей, представляющих собой систему взаимосвязанных уравнений регрессии, разделение переменных на объясняющие и зависимую, принятое в регрессионном анализе, теряет смысл, т. к. одна и та же переменная может входить в одно из уравнений как зависимая, а в другое - как объясняющая. Поэтому следует говорить о классификации переменных, которая соответствует сущности и особенностям эконометрических моделей.

Такое разделение переменных относится к проблеме спецификации моделей и исходит из экономических и логико-теоретических соображений ( 3, с. 63). Поэтому классификация должна отражать объективно существующие отношения между изучаемыми экономическими явлениями, вскрывая их природу и характер с выделением взаимозависимых явлений и односторонних зависимостей.

• 1 . Эндогенные переменные, т. е. экономические величины, которые являются зависимыми и объясняются эконометрической моделью. Значения этих переменных формируются в результате одновременного взаимодействия переменных, образующих модель. Эндогенные переменные зависят от экзогенных и возмущающих переменных.
• 2. Экзогенные переменные, определяемые вне модели. Они не объясняются моделью и являются внешними, заданными экономическими величинами. Между эндогенными и экзогенными переменными существуют только односторонние стохастические причинные отношения.
• 3 . Лаговые переменные, значения которых отстают на один или несколько периодов. Поскольку лаговые переменные в период времени t также не объясняются эконометрической моделью, то их можно отнести к заранее заданным экзогенным.

А. Предопределенные переменные, к которым относятся:

• а) обычные экзогенные переменные, они заранее предопределены, так как объясняются фактами, лежащими вне модели;
• б) лаговые экзогенные переменные, они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;
• в) лаговые эндогенные переменные, их предопределенность следует из предшествующего объяснения в эконометрической модели.
• 5. Совместно зависимые переменные, которые определяются нс одним уравнением, а одновременными уравнениями модели. Эконометрическую модель в связи с этим можно рассматривать как способ определения совместно зависимых переменных через предопределенные переменные и возмущения.
• 6. Возмущающие или латентные переменные, т. с. экономические величины, не входящие в уравнения эконометрических моделей, но оказывающие влияние на совместно зависимые переменные. Возмущения являются стохастическими переменными. В отличие от совместно зависимых и предопределенных переменных, их эмпирические значения неизвестны, они находятся как остатки по определенным уравнениям после оценки неизвестных параметров модели. Интерпретация возмущающих переменных в эконометрической модели та же, что и в случае одного уравнения регрессии, рассмотренного в главе 4.

                         

14. Расчет стандартных ошибок параметров уравнения парной регрессии и точности прогнозирования.

Для расчета дисперсий D(a) и D(в) коэффициентов регрессии а и в в формулах использовалась дисперсия σ ² случайного члена ε. Эта дисперсия неизвестна, но ее можно оценить, используя выборочные данные. Можно доказать, что несмещенной оценкой дисперсии σ ² является величина S², где:

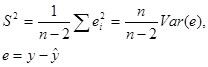(10)

Величина S называется стандартной ошибкой регрессии. Она служит мерой разброса зависимой переменной около линии регрессии. Запишем в формулах (9) дисперсию σ ² ее оценкой S²:

(11)

и 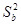называют оценками дисперсии коэффициентов регрессии, а величина Sa и Sв – стандартными ошибками коэффициентов регрессии. Они используются для построения доверительных интервалов, которым принадлежат параметры истинной регрессии и для проверки значимости коэффициентов регрессии.

Прогнозирование на основе эконометрических моделей является одной из основных задач эконометрики.

Под прогнозированием в эконометрике понимают построение оценки зависимой переменной для таких значений независимых переменных, которых нет в исходных наблюдениях.

Различают точечное прогнозирование и интервальное.

Точечный прогноз это число, значение зависимой переменной, вычисляемое для заданных значений независимых переменных.

Интервальный прогноз это интервал, в котором с заданным уровнем значимости ( с заданной вероятностью) находится истинное значение зависимой переменной для заданных значений независимых переменных.

Рассмотрим парную линейную регрессионную модель и соответствующее выборочное уравнение регрессии 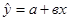. Обозначим через у_р истинное значение переменной у для заданного значения независимой переменной х_р, т. е. .

Точечным прогнозом для у_р является , т. е. чтобы получить точечный прогноз нужно в построенное уравнение регрессии подставить заданное значение независимой переменной.

Ошибкой предсказания ( ) называют разность между прогнозным и истинным значениями независимой переменной.

Можно доказать, что дисперсия ошибки предсказания

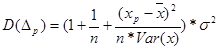. (21)

Из (21) следует, что чем ближе заданное значение независимой переменной к тем меньше дисперсия прогноза и чем больше объем выборки n, тем меньше дисперсия прогноза.

Заменив в (21) дисперсию 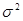на ее оценку 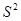, извлечем, квадратный корень и получим стандартную ошибку предсказания .

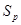(22)

Выберем уровень значимости α и по таблице распределения Стьюдента найдем t_кр. Тогда с вероятностью 1- α истинное значение переменной у_р будет находится внутри интервала:

 

 

Очевидно, что чем ближе к и чем больше n, тем уже доверительный интервал (тем точнее прогноз). Это надо учитывать, выбирая прогнозные значения для независимой переменной.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: