12. Автокорреляция случайных возмущений, их последствия, взвешенный метод наименьших квадратов. 

Автокорреляция случайных возмущений означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε _t ε _S) = 0, при t ≠ s) гарантирует некоррелированность значений случайных членов в раз­личные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени на­зывается автокорреляцией (сериальной корреляцией).

Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); наличие неучтенных факторов; использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды).

Для проверки на автокорреляцию используется ряд крите­риев, из которых наиболее широкое применение получил крите­рий Дарбина-Уотсона

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяются следующие:

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок
2. Дисперсии оценок являются смещенными. Зачастую дисперсии, вычисляемые по стандартным формулам, являются заниженными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.

Оценка дисперсии регрессии 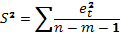является смещенной оценкой истинного значения , во многих случаях занижая его.

В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

Формулировка взвешенного метода наименьших квадратов (ВМНК). Для того, чтобы его сформулировать достаточно обобщить те процедуры, которые предпринимались для оценки параметров линейной модели в условиях гетероскедастичности:

• 1) подбирается функция , с помощью которой моделируется зависимость дисперсии случайных возмущений от суммарного веса регрессоров в уравнениях наблюдений;
• 2) все переменные в каждом наблюдении умножаются на ;
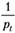• 3) к преобразованной таким образом выборке применяется метод наименьших квадратов для получения оценок параметров модели.

Как это выглядит математически? Введем матрицу W размерностью ( ):

(7. 15)

Тогда преобразование переменных можно представить в виде произведений: и , процедура метода наи

меньших квадратов примет вид:

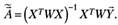(7. 16)

Процедура (7. 16) обеспечила получение состоятельных оценок параметров линейной модели при выполнении всех предпосылок теоремы Гаусса – Маркова, кроме второй предпосылки о гомоскедастичности случайных возмущений.

Этот факт нашел свое отражение в теореме. Прежде, чем ее сформулировать, введем матрицу ковариаций вектора случайных возмущений в виде

(7. 17)

Теорема. Если в схеме Гаусса – Маркова ковариационная матрица вектора случайных возмущений имеет вид (7. 17), то оптимальной процедурой, доставляющей состоятельные оценки параметров линейной модели, является

(7. 18)

Процедура (7. 18) называется взвешенным методом наименьших квадратов.