15. Теорема Гаусса-Маркова, основные допущения и предпосылки, их практическое содержание и назначение. 

15. Теорема Гаусса-Маркова, основные допущения и предпосылки, их практическое содержание и назначение.                                                                                        

            Теорема Гаусса-Маркова формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпоссылками теоремы Гаусса-Маркова.

И так. Если:

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю:

2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе :

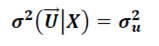
3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы):

4. Ковариация между вектором регрессоров и вектором случайных переменных равн нулю ( регрессоры и случайные возмущения независимы):

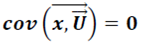
Тогда. Если матрица Х неколлинеаная:

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как:

Она соответствует методу наименьших квадратов

2. Ковариационная матрица оценок параметров модели вычисляется как:

3. Дисперсия случайного возмущения равна:

4. Наилучший прогноз модели в точке 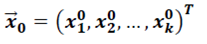вычисляется по правилу:

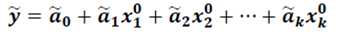
5. Ошибка прогноза эндогенной переменной равна:

            Вернемся к задаче оценки параметров уравнения парной регрессии и решим ее с помощью процедур, сформулированных в теореме Гаусса-маркова.

Имеем уравнени парной линейной регрессии:

Выборку наблюдений объемом n за поведением экономического объекта

Сформулируем необходимые вектора и матрицу коэффициентов уравнений наблюдений:

Столбец из единиц появился в матрице, в связи с тем, что в спецификации присутствует параметр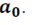

Вот все необходимое для оценки модели

Выражение позволяет вычислить оценки параметров. Для этого вначале вычисляется произведение матриц:

Матрица обратная к этой есть

Вычисляется произведение

Подставляя выражение в последние два произведения в исходное выражение получим вектор оценок параметров линейной модели парной регресии

 

16. Нелинейная регрессия. Нелинейные модели и их линеаризация.        

После отбора объясняющих переменных X = (хих2,..., хк)т и результативного показателя у решается задача выбора параметрического семейства функций /(Х, Р), при этом линейные уравнения регрессии не всегда дают удовлетворительные результаты при анализе зависимостей. В силу сложности экономических зависимостей их моделирование возможно лишь на основе нелинейных моделей регрессии. Например, нелинейными являются [2, 29]:

• • производственная функция Кобба – Дугласа, которая отражает зависимость между объемом произведенной продукции и основными факторами производства – трудом и капиталом;
• • функция спроса, определяющая зависимость спроса на товары или услуги от цены и среднедушевого дохода семьи.

При этом выбор вида зависимости должен осуществляться на основании содержательного анализа исследуемого явления.

Различают два класса нелинейных регрессионных моделей.

1. Нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам ( ). Например, полиномиальная модель:

2. Нелинейные как относительно включенных в анализ объясняющих переменных, так и по оцениваемым параметрам. Например, степенная модель регрессии:

Если в результате предварительного анализа определяют вид нелинейной зависимости результативного показателя у от объясняющих переменных 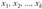, то стараются линеаризовать уравнение, т. е. преобразовать нелинейную зависимость в линейную. Для оценки параметров нелинейных моделей используют два подхода.

Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую нелинейную зависимость представляют в виде линейной между преобразованными переменными.

Второй подход, основанный на применении методов нелинейной оптимизации, применяется в том случае, когда подобрать соответствующее преобразование не удается. Рассмотрим такие методы линеаризации нелинейных моделей, как замена переменных; логарифмирование обеих частей уравнения и комбинированные методы.

Суть первого метода состоит в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Например, полиномиальная модель к-го порядка 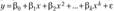может быть приведена к линейному виду путем замены переменных 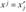. После замены переменных получим линейную регрессионную модель вида .

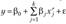Таким образом, полином любого порядка сводится к линейной модели регрессии, для которой нами уже рассматривались методы оценивания параметров и проверки гипотез.

Среди нелинейных полиномиальных регрессионных моделей чаще всего используются параболические модели второго и третьего порядка. Ограничения в использовании полиномов более высоких порядков связаны с содержательной интерпретацией коэффициентов регрессии.

Оценка неизвестных коэффициентов в мультипликативных моделях регрессии требует предварительного логарифмирования обеих частей уравнения и замены переменных для ее преобразования к линейному виду.

В степенных моделях вида

которые широко используются в эконометрических исследованиях, после логарифмирования левой и правой частей уравнения и замены переменных и , получим линейную модель регрессии относительно новых переменных 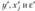, а именно:

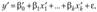
где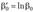

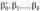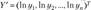При оценке параметров с помощью метода наименьших квадратов (МНК) вектор-столбец Y' и матрица X' определяются по исходным наблюдениям { }, где , следующим образом: , a j-й столбец матрицы X' есть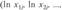 , (напомним, что первый столбец матрицы X' составлен из одних единиц).

К классу степенных функций относятся кривые спроса и предложения, производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий.

Если степенная функция отражает зависимость объема выпуска продукции у от использования ресурса. г (в которой ), то она называется производственной функцией. Например, производственная функция Кобба – Дугласа связывает объем производства У с затратами капитала (К) и труда (L):

Автономная зависимость от времени выражена в коэффициенте научно- технического прогресса А. Показатели а и (3 являются коэффициентами частной эластичности объема производства У соответственно по затратам капитала К и груда L. Это означает, что при увеличении затрат капитала (труда) на 1% объем производства в среднем увеличивается на а. % ((3%) при неизменности затрат труда (капитана).

Сумма коэффициентов является важным экономическим показателем, который носит название отдача от масштаба. При а + (3 > 1 имеет место возрастающая отдача от масштаба (увеличение объема выпуска больше увеличения затрат ресурсов); при а + (3 < 1 – убывающая отдача от масштаба (увеличение объема выпуска меньше увеличения затрат ресурсов). При а + (3 = 1 говорят о постоянной отдаче от масштаба (во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается выпуск). Функцию Кобба – Дугласа можно также представить в виде

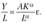
Таким образом, получается зависимость производительности труда (УД) от капиталовооруженности (K/L). Для оценки параметров данной модели ее логарифмируют с целью приведения к линейному виду (для i-го наблюдения):

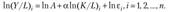
Рассмотренные степенные модели регрессии являются нелинейными относительно оцениваемых параметров, так как включают параметры аир мультипликативно. Однако их можно считать внутренне линейными, так как логарифмирование уравнения приводит его к линейному виду.

Широкое использование в экономических исследованиях степенных моделей во многом связано с четкой интерпретацией их параметров (3(. В этих моделях (3( являются коэффициентами эластичности, которые показывают, на сколько процентов в среднем изменится результативный признак у, если факторный признак х, увеличится на 1%.

О правомерности подобного толкования параметра b для степенной функции у = ахь можно судить, если рассмотреть формулу расчета коэффициентов эластичности

где /'(х) – первая производная, характеризующая соотношение приростов результативной и факторной переменных для соответствующей формы связи. Для степенной функции она составит f'(x) = abxh~l. Соответственно коэффициент эластичности равен

Таким образом, для степенной функции коэффициент эластичности представляет собой постоянную величину, равную параметру Ь. В других функциях коэффициент эластичности зависит от значений фактора х. Так, для линейной регрессии первая производная и эластичность функции уых = а + bх следующие:

В силу того что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения д*, обычно рассчитывается средний показатель эластичности по формуле

Пример 4. 3 [3, 29]

Построим по данным Великобритании за п = 20 лет степенные регрессионные модели объема потребления мяса цыплят (у) в зависимости от среднедушевого дохода (. г, ), стоимости 1 фунта цыплят (лг2), стоимости 1 фунта свинины (. v3) и стоимости 1 фунта говядины (. г4). Исходные данные представлены в табл. 4. 4.

Таблица 4. 4

Исходные данные для примера 4. 3

t	У
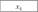
	30. 8	459, 7	39. 5	55, 3	79, 2
	31. 2	492, 9	37, 3	54, 7	77. 4
	33, 3	528, 6	38, 1	63, 7	80, 2
	35. 6	560, 3	39, 3	69, 8	80, 4
	36. 4	624, 6	37, 8	65, 9	83, 9
	36, 7	666, 4	38, 4	64, 5	85, 5
	38, 4	717, 8	40, 1	70. 0	93, 7
	40, 4	768. 2	38, 6	73, 2	106, 1
	40. 3	843, 3	39, 8	67, 8	104, 8
	41, 8	911, 6	39, 7	79, 1	114, 0
	40, 4	931. 1	52. 1	95, 4	124, 1
	40. 7	1021. 5	48. 9	94, 2	127, 6
	40, 1	1165, 9	58. 3	123, 5	142, 9
	42, 7	1349, 6	57. 9	129, 9	143, 6
	44. 1	1449, 4	56, 5	117, 6	139, 2
	46. 7	1575. 5	63. 7	130, 9	165, 5
	50. 6	1759, 1	61, 6	129, 8	203, 3
	50. 1	1994. 2	58, 9	128, 0	219, 6
	51, 7	2258. 1	66. 4	141, 0	221, 6
	52. 9	2478, 7	70. 4	168, 2	232, 6

Требуется построить и сравнить следующие степенные уравнения регрессии:

• а) – функция спроса;
• б) – функция потребления;
• в) – функция спроса и потребления;
• г) 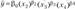– функция спроса с учетом цены на товарозамени- тели.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: