18. Понятие адекватности экономических моделей. Проверка статистической гипотезы об адекватности модели.

https: //studall. org/all4-3719. html

https: //studopedia. ru/9_148075_fiktivnie-peremennie-i-osobennosti-ih-ispolzovaniya-v-modelyah. html

18. Понятие адекватности экономических моделей. Проверка статистической гипотезы об адекватности модели.

Под адекватностью понимается возможность получения результата с удовлетворительной точностью. Очевидно, чтобы оценить точность прогноза, необходимо сопоставить вычисленное по модели прогнозное значение эндогенной переменной с ее реальным значением при одинаковых значениях набора регрессоров. Если разница между этими значениями по абсолютной величине окажется приемлемой, то можно будет сделать вывод об адекватном описании поведения объекта полученной моделью.

Шаг 1. Имеющаяся выборка делится на две неравные части. Первая объемом 5% - 10% от общего объема выборки, вторая – все остальное. Первую выборку называют контрольной, вторую – обучающей. Из названия понятно, что первая (маленькая) выборка предназначена для тестирования модели на адекватность, вторая (большая) предназначена для оценивания модели.

Шаг 2. По обучающей выборке проводится идентификация модели.

Шаг. 3. Используя полученные значения оценок параметров модели, вычисляются значения оценок эндогенной переменной для каждой точки контрольной выборки.

Шаг 4. Формулируется статистическая гипотеза о равенстве реального и прогнозного значений эндогенной переменной в каждой точке контрольной выборки H₀ : 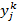= . Индекс k указывает на принадлежность контрольной выборке, индекс j порядковый номер точки в контрольной выборке.

Шаг 5. Вычисляется значение дроби Стьюдента t_j= и проверяется выполнения условия, что t_j= ≤ t_крит. Если условие выполняется в каждой точке контрольной выборки, то делается вывод об адекватности модели с доверительной вероятностью Рдов.

                                                                                          

19. Проверка статистических гипотез. Оценка статистической значимости параметров уравнения множественной регрессии.

Определение. Под статистической гипотезой понимается любое предположение о виде закона распределения случайной величины или значениях его параметров

Примеры статистических гипотез:

Н₀: (U имеет нормальный закон распределения)

H₀: (параметр а₀=0)

Н₁: (параметр а₀=1)

Гипотезы H₀ и H₁ называются основной и альтернативной

Алгоритм проверки статистических гипотез:

• Формулируется статистическая гипотеза H₀
• Искусственно формируется случайная величина «Z», закон распределения которой известен [P_z(t, a₁, a₂)], котoрая тесно связана с гипотезой
• Область допустимых значений Z делится на две части: Ω ₀ в которой гипотеза принимается и, Ω в которой она отклоняется
• Граница этих областей определяется из условия, что Z попадает в область Ω ₀ с заданной вероятностью «р»
• По данным выборки вычисляется значение случайной величины Z и проверяется ее принадлежность область Ω ₀

Возможные ошибки при проверке статистических гипотез:

Ошибка первого рода - когда справедливая гипотеза отклоняется

Ошибка второго рода - когда ложная гипотеза принимается

Оценка статистической значимости параметров уравнения множественной регрессии:

1. Известно, что в схеме Гаусса – Маркова дроби:

называются дробью Стьюдента и подчиняются закону распределения Стьюдента

Критическое значение дроби Стьюдента находится из уравнения:

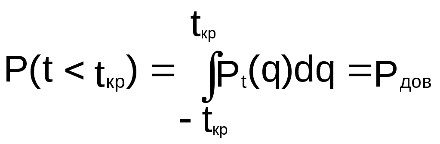
Здесь: P_t(q) функция плотности вероятности распределения Стьюдента, t_кр – двусторонняя квантиль распределения, Р_дов- значение доверительной вероятности, как правило Р_дов=0. 95/0. 99

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: