 |
Как найти значение tкр?. 20. Тестирование моделей на присутствие автокорреляции.. 21. Требования, предъявляемые к оценкам параметров моделей,
|
|
|
|
Как найти значение tкр?
В EXCEL используется функция СТЬЮДРАСПОБР с аргументами: «α =(1-Рдов) – мощность критерия и «m» - количество степеней свободы
Гипотеза Н0{ai=c} не отклоняется, если выполняется условие:
Условие называется точечной проверкой гипотезы
Из условия получают границы доверительного интервала для значений дроби Стьюдента:
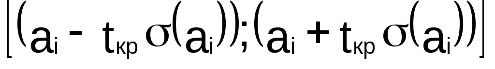
Если константа C лежит внутри этого интервала, то гипотеза о равенстве оценки ai константе С не отвергается
2. В схеме Гаусса-Маркова переменная:
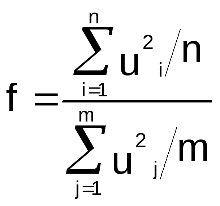
подчиняется закону распределения Фишера и критическое значение этой дроби вычисляется из условия:
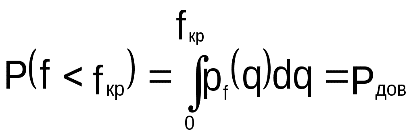
Закон распределения вероятностей Фишера имеет два параметра: n и m, которые называются степенями свободы
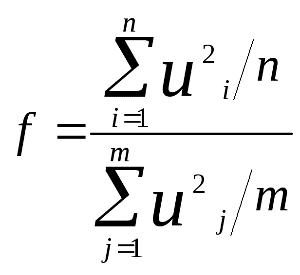
+В EXCEL используется процедура функция FРАСПОБР:
FРАСПОБР(α; n; m)
где α – мощность критерия
20. Тестирование моделей на присутствие автокорреляции.
Автокорреляция – зависимость возмущений в различные моменты времени
Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui, uj)≠ 0 при i≠ j
Для проверки наличия (либо отсутствия) автокорреляции широкое применение получил тест Дарбина-Уотсона.
Предпосылки теста:
- Случайные возмущения распределены по нормальному закону
- Имеет место авторегрессия первого порядка:
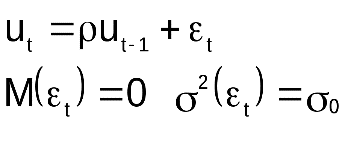
Статистика для проверки гипотезы:
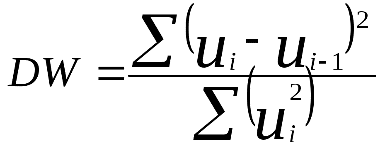
Свойства статистики DW:
где: r - коэффициент корреляции между случайными возмущениями
Из этого выражения следует:
DW изменятся в пределах (0 – 4)
При этом если r = 1, DW=0 - положительная корреляция
|
|
|
если r = 0, DW=2 - отсутствие корреляции
если r=-1, DW=4 - отрицательная корреляция
Особенности статистики DW:
Для статистики DW не возможно найти критическое значение, т. к. оно зависит не только от Рдов и степеней свободы k и n, но и от абсолютных значений регрессоров
Возможно определить границы интервала DL и Du внутри которого критическое значение DWкр находится:
DL ≤ DWкр ≤ Du
Значения Du и DL находятся по таблицам
21. Требования, предъявляемые к оценкам параметров моделей,
Чтобы правильно и точно оценить параметры модели, оценки должны быть: несмещенными, состоятельными, эффективными и достаточными.
Оценки b являются несмещенными , если их математические ожидания равны истинным значениям параметров:
M[b]=b.
Это значит, что в процессе вычисления параметров модели не должны возникать статистические ошибки.
Оценка называется состоятельной, если при увеличении числа наблюдений n до бесконечности она сходится по вероятности к истинному параметру:
Достаточное условие для этого
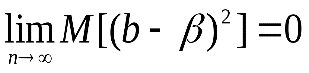
Оценки будут эффективными, если они позволяют получить максимальную информацию из наблюдений. Часто бывает, что из исследуемого параметра можно найти несколько состоятельных оценок. Чтобы выбрать одну из них сравнивают дисперсии всех оценок и по минимуму дисперсии получают оценку, которая и будет эффективной
,
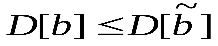где D[b] - дисперсия оценки b,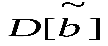 
- дисперсия любых других несмещенных оценокb.
Пример. Дано n наблюдений случайной величины X. Возникает вопрос, какую величину принять за оценку математического ожидания: среднее выборки или медиану. Известно, что величина X распределена по нормальному закону с дисперсиям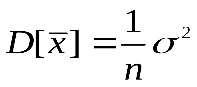и: 
и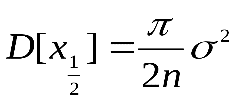 
,
где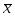 
- среднее выборки; 
- медиана; n - объём выборки; 
- дисперсия генеральной совокупностиX. Так как 
, то оценка средней выборки будет эффективной.
Критерии несмещенности и эффективности следует рассматривать одновременно. Может оказаться, что смещенная оценка с меньшей дисперсией будет более предпочтительной, чем несмещенная оценка с большей дисперсией.
|
|
|
Существует несколько различных методов оценивания параметров:
· максимального правдоподобия;
· моментов;
· оценивание по Байесу;
· наименьших квадратов.
|
|
|
