22. Классификация переменных эконометрических моделей,

22. Классификация переменных эконометрических моделей,        

При построении эконометрических моделей, представляющих собой систему взаимосвязанных уравнений регрессии, разделение переменных на объясняющие и зависимую, принятое в регрессионном анализе, теряет смысл, т. к. одна и та же переменная может входить в одно из уравнений как зависимая, а в другое - как объясняющая. Поэтому следует говорить о классификации переменных, которая соответствует сущности и особенностям эконометрических моделей.

Такое разделение переменных относится к проблеме спецификации моделей и исходит из экономических и логико-теоретических соображений ( 3, с. 63). Поэтому классификация должна отражать объективно существующие отношения между изучаемыми экономическими явлениями, вскрывая их природу и характер с выделением взаимозависимых явлений и односторонних зависимостей.

1 . Эндогенные переменные, т. е. экономические величины, которые являются зависимыми и объясняются эконометрической моделью. Значения этих переменных формируются в результате одновременного взаимодействия переменных, образующих модель. Эндогенные переменные зависят от экзогенных и возмущающих переменных.

2. Экзогенные переменные, определяемые вне модели. Они не объясняются моделью и являются внешними, заданными экономическими величинами. Между эндогенными и экзогенными переменными существуют только односторонние стохастические причинные отношения.

3 . Лаговые переменные, значения которых отстают на один или несколько периодов. Поскольку лаговые переменные в период времени t также не объясняются эконометрической моделью, то их можно отнести к заранее заданным экзогенным.

А. Предопределенные переменные, к которым относятся:

а) обычные экзогенные переменные, они заранее предопределены, так как объясняются фактами, лежащими вне модели;

б) лаговые экзогенные переменные, они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;

в) лаговые эндогенные переменные, их предопределенность следует из предшествующего объяснения в эконометрической модели.

5. Совместно зависимые переменные, которые определяются нс одним уравнением, а одновременными уравнениями модели. Эконометрическую модель в связи с этим можно рассматривать как способ определения совместно зависимых переменных через предопределенные переменные и возмущения.

6. Возмущающие или латентные переменные, т. с. экономические величины, не входящие в уравнения эконометрических моделей, но оказывающие влияние на совместно зависимые переменные. Возмущения являются стохастическими переменными. В отличие от совместно зависимых и предопределенных переменных, их эмпирические значения неизвестны, они находятся как остатки по определенным уравнениям после оценки неизвестных параметров модели. Интерпретация возмущающих переменных в эконометрической модели та же, что и в случае одного уравнения регрессии.

В зависимости от цели исследования и поставленных задач эконометрическая модель может быть представлена в различных видах.

Основы регрессионного анализа, рассмотренные в главе 4, содержат основные понятия, предпосылки и методы эконометрического моделирования. Однако во многих случаях в экономике приходится иметь дело с необходимостью описания и измерения системы причинных отношений.

Структурная форма модели.

Она отражает одно- и многосторонние стохастические причинные отношения между экономическими величинами в их непосредственном виде.

Эта система уравнений, отражающих наличие одновременных экономических взаимосвязей, называется системой одновременных или структурных уравнений. В структурном уравнении содержится одна или несколько совместно зависимых переменных. Характерной особенностью структурных уравнений является определенная автономность их по отношению к предопределенным переменным, так как изменение этих переменных и их параметров в одном структурном уравнении не обязательно приводит к изменениям в других структурных уравнениях.

Наряду со структурными уравнениями эконометрическая модель может содержать так называемые определяющие уравнения - тождества. Тождества не содержат возмущений и их параметры в общем случае равны единице, следовательно, они не подлежат оценке. Примером может быть следующая модель: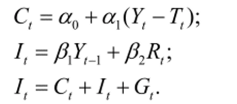